• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ОПЕРАТОРНИЙ МЕТОД АНАЛIЗУ ЛЕК

Iдея операторного методу полягає в тому, що з областi функцiй дiйсного змiнного 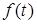розв'язання задачі аналізу переноситься до областi функцiй 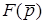комплексного змiнного .

Iнтегральне перетворення Лапласа дозволяє перетворити 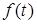у :

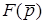. (8.1)

Формула (8.1) є прямим перетворенням Лапласа. Функцiя 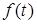зветься оригiналом, а функцiя 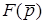- зображенням.

Не всi функцiї можуть знаходитись у просторi оригiналiв. На 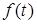накладаються такі обмеження:

1) 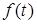- кусково-неперервна;

2) (функцiя тотожно дорiвнює нулю при вiд'ємних значеннях t);

3) , де М i 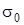- позитивнi дiйснi сталi. Тобто 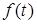збiльшується не швидше показникової функцiї (має обмежене зростання).

Друга умова виконується зсувом початку вiдлiку. Перша i третя умови завжди виконуються для реального генератора. Отже, функцiї, якi описують реально можливi дiї i тим бiльш вiдповiднi до них реакцiї, завжди можуть бути перетворенi за Лапласом.

Iнтегральне перетворення Лапласа має двi основнi властивостi: єдинiсть та лiнiйнiсть.

Перша означає, що мiж зображенням та оригiналом iснує взаємоодно-значна вiдповiднiсть: якщо , то .

Друга властивiсть дозволяє застосувати принцип суперпозицiї:

Якщо , то .

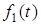Загальна схема операторного способу визначення вiдгуку , якщо вiдома дія , має вигляд:

Простiр оригiналiв Простiр зображень

® ® ® ® ® ®

¯

¬ ¬ ¬¬ ¬ ¬

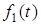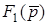
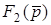
Перевага операторного методу полягає у тому, що у просторi оригiналiв операцiї приймають простiший вигляд, а саме: замiсть вихiдних iнтегро-диференцiйних рiвнянь отримують алгебраїчнi рiвняння; далi розв'язуються алгебраїчнi рiвняння в областi 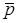; потiм результат, що отримано, переводиться знову до простору оригiналiв.

Розглянемо бiльш докладно етапи розв'язання.

1. Перехiд вiд 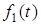до .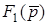

Виконується трьома основними способами:

1) за формулою прямого перетворення Лапласа. Наприклад, якщ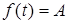о , то

.

Якщо ,

.

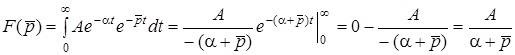2) за таблицями, якi попередньо розраховано i наведено у довiдниках;

3) використовуючи властивостi перетворення Лапласа, якi сформульовано у теоремах. Основнi теореми такi:

а) теорема диференцiювання оригiналу:

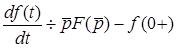, (8.2)

де 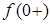- значення функцiї, яку диференціюють, в точцi 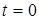при наближеннi до неї справа.

За нульових початкових умов .

б) теорема iнтегрування оригiналу

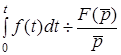; (8.3)

в) теорема зсуву оригiналу (теорема запiзнення)

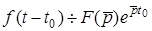; (8.4)

г) теорема зсуву зображення

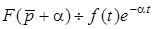. (8.5)

2. Перехiд вiд 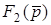до . Також виконується кiлькома способами:

1) за таблицями;

2) за теоремою розкладання.

Згiдно з цiєю теоремою, якщо 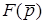має вигляд рацiонального дробу , де 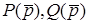- степеневі полiноми, причому степiнь чисельника менша за степiнь знаменника i 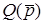має n рiзних коренiв, тобто , тодi

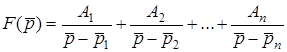, (8.6)

де .

У цьому випадку оригiнал кожного з доданкiв (8.6) є експонентою. Формула (8.6) справедлива для простих (непарних) коренiв. Для парних коренiв теорема розкладання ускладнюється.

3) за формулою оберненого перетворення Лапласа

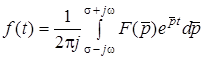. (8.7)

Безпосередньо формулою (8.7) не користуються. Якщо , то 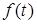обчислюється як сума лишкiв

.

Лишки визначаються в особливих точках

.

Розглянемо як приклад коло, яке складається з послiдовно з’єднаних опору та iндуктивностi. До кола вмикається джерело постiйної е.р.с. E. Пiсля замикання ключа коло описується диференцiйним рiвнянням

.

Нехай функцiї вiдповiдає зображення 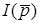. За теоремою диференцiювання в областi 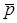рiвняння приймає вигляд

.

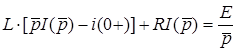За нульових початкових умов (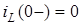) матимемо . Отже, отримуємо алгебраїчне рiвняння , з якого знайдемо .

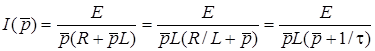Скористаємось теоремою розкладання:

,

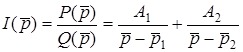де ;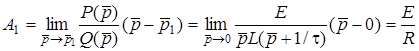

.

Отже, .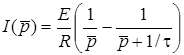

Для переходу вiд зображення 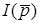до оригiналу скористаємось властивiстю лiнiйностi та формулами вiдповiдностi, які розглянуто вище:

.

8.1 Закон Ома i закони Кiрхгофа в операторнiй формi.

Нульовi початковi умови

Розглянемо як приклад послiдовний коливальний контур, до якого увімкнено джерело е.р.с.

Дано: ; 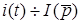. Початковi умови нульовi: ; .

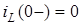Згiдно з другим законом Кiрхгофа ; 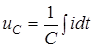. Подамо напругу на ємностi у виглядi двох iнтегралiв:

.

Тодi

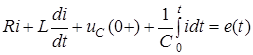. (8.8)

Перетворимо (8.8) за допомогою прямого перетворення Лапласа:

.

Вiдповiдно до законiв комутацiї за нульових початкових умов 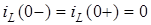; . Тодi

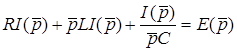. (8.9)

Позначивши ; ; 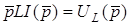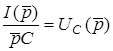, матимемо запис другого закону Кiрхгофа в операторнiй формi:

. (8.10)

Позначимо 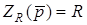- операторний опiр резистора;

- операторний опiр iндуктивностi;

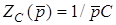- операторний опiр ємностi.

Слiд зазначити, що при , 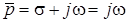; ; 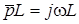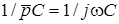, тобто комплекснi опори ємностi та iндуктивностi - окремий випадок операторного опору.

Якщо винести 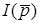у формулi (8.9) за дужки, отримаємо

,

де 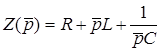- операторний опiр кола. Тодi матимемо закон Ома в операторнiй формi:

. (8.11)

Розглянемо перший закон Кiрхгофа в операторнiй формi на прикладi кола, яке складається з паралельно з’єднаних опору, ємностi та iндуктивностi. Згiдно з цим законом загальний струм i становить:

; .

Аби застосувати перетворення Лапласа, розпишемо

.

Тодi .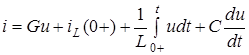

Враховуючи, що 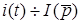; 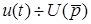, матимемо

.

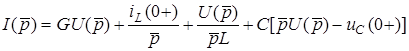Оскiльки початковi умови нульовi (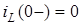; ), то

. (8.12)

Позначивши ; ; 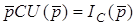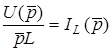, отримуємо запис першого закону Кiрхгофа в операторнiй формi

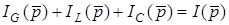. (8.13)

Згiдно з цим законом сума зображень струмiв, якi входять до вузла, дорiвнює сумi зображень струмiв, що витiкають з вузла.

Iнакше (8.12) можна записати

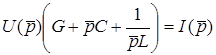, (8.14)

де 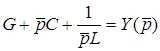- операторна провiднiсть кола.

З (8.14) отримуємо закон Ома в операторнiй формi

.

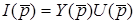Пiдсумок. За нульових початкових умов етап складання системи диференцiйних рiвнянь для кола, що аналiзується, та її перетворення можна замiнити складанням системи алгебраїчних рiвнянь i розв'язанням цієї системи стандартними методами теорiї кiл в операторнiй формi.

Читайте також:

1. D) методу мозкового штурму.
2. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
3. I Метод Шеннона-Фано
4. I. Метод рiвних вiдрiзкiв.
5. VII. Нахождение общего решения методом характеристик
6. А. науковий факт, b. гіпотеза, с. метод
7. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
8. Агрегативна стійкість, коагуляція суспензій. Методи отримання.
9. АгротехнІЧНИЙ метод
10. Адаптовані й специфічні методи дослідження у журналістикознавстві
11. Адміністративні (прямі) методи регулювання.
12. Адміністративні методи - це сукупність прийомів, впливів, заснованих на використанні об'єктивних організаційних відносин між людьми та загальноорганізаційних принципів управління.

Переглядів: 700