Instructions of data handling

This group of instructions is the greatest and the most important. It is divided depending on operations which are executed over the data:

1. arithmetic;

2. logic;

3. instructions of shifting;

4. instructions of lines handling.

1. Basic arithmetic instructions are intended for the arithmetic operations over some operands setting. Any arithmetic operation is a two-seater (example: ADD dst,src; Chart of calculations: dst:=(dst)*(src) (dst)*(src)Þdst).

If to use the accumulator principle ACC:=(ACC)*(src). The instructions of arithmetic operations form practically always the signs of operations result. A base arithmetic operation is arithmetic addition(addition of binary codes, because the addition without sign). Majority COMPUTERS are not limited by the addition operation, there is yet deduction of binary codes (SUB dst,src). This operation is not commutative. The deduction command of binary codes provides deduction without sign codes. But formulating properly codes it is possible to process data with a sign. If to process the multybytes data, as a number system is binary position, treatment is begun with the least significant bit. As a rule, for these cases there are special commands (ADC dst,src; SBB dst,src; Chart of calculations: dst:=(dst)*(src) ± (CY)).

If the operands of different length can participate in arithmetic operations, preliminary a short operand is increased to the length of long (for integer arithmetic), thus right-aligning goes here, and expansion goes by a sign. It can be realized automatically, or due to the commands of sign expansion (SXT). As a rule, expansion of instruction takes a place in the fixed register, consequently, these instructions are zeroaddress. If it is not present, it is needed to write the special procedures of expansion. Operation of codes comparison(CMP dst,src). By the contents it is an instruction of deduction. Actually chart of calculation is: (dst) -(src). All of result signs on this instruction are formed, and a result is nowhere saved.

One operandarithmetic instructions. As the fixed value (as a rule, it is =1) has the second operand, then command INC dst; DEC dst;, and charts of calculations dst:=(dst)±1. These commands are very in-use at development of counters, indexes. Not applicable for many bytes data, allow to save signs for next branches. Instructions of multiplication and division.In the instruction sets of small COMPUTERS these commands absent, but if they are present in the instruction set, they are used for the data without sign. Command format: MUL dst,src; DIV dst,src; For the product storage the fixed registers are usually used, more frequent than all it is an accumulator with an extender. Like for an integer division. In general case a dividend has double length, consequently, as a rule, a receiver of result is also the fixed register (accumulator with an extender). Very often in the instruction sets enter the commands of multiplicationand division taking into account a sign (IMUL dst,src; IDIV dst,src;). These commands are usually oriented on the base computer formats usage. For the many bytes data handling at the multiplication and division, at first the decomposition is made, and then multiplication or division of many bytes data can be build. If a machine is oriented to the scientifically technical calculations, operations are required over the data with a floating point and they are present there. As a rule in small COMPUTERS commands with floating arithmetic are not presented. But operations of addition and deduction executed by psubprograms or by a subprocessor. Instructions of decimal arithmetic.Basis of decimal arithmetic in any COMPUTERS is made by the instructions of binary arithmetic. Usually to these instructions belonge the decimal correction instructions. Usually these instructions depend on that, what format is used (packed or unpacked). Independently to a format, instructions are based on the accumulator method (it means that the instructions of decimal correction are zeroaddressed). In this case decimal treatment consists of two phases: 1) proper binary action 2) correction taking into account a decimal number.

2. Instructions of logical operations. Logical instructions in the instructions set of COMPUTER play not only an additional role, but in logical tasks can be the basic statements of handling. For this purpose the system of logical operations in COMPUTER must be functionally complete. As a rule, the redundant boolean operations are built-in to the instructions set. Operations are executed bit-by-bit and simultaneously from the right to the left. Instructions of logical handling are one and two operands. A single-seat operation will be realized by the negation: NOT dst; Chart 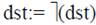. Two operands boolean operations will realize: &, ∪, ⊕. AND dst,src; OR dst,src; XOR dst,src; dst:=(dst)*(src);. More frequent than all boolean operations are used for the decision of three tasks.

1. Masking and selection of certain bits of operands. Realized by the operation of conjunction (&) with the set mask

2. Required values forming in the required bits (with a help ∪).

3. Inverting of certain bits (with a help ⊕)

Boolean operations preferentially influence on flags, it means that part of flags after operation implementation does not change (OVR:=0; CY:=0), some of them can have an indefinite value (AF:=?). In the instructions set of boolean operations there are some instructions (TEST dst,src; Chart (dst)&(src)). In investigation of this operation implementation, a result is nowhere written, but all of flags are formed.

3. Commands of shifting. All of the realized instructions of shifting can be divided by signs:

1. kind of shifting (arithmetic or logical)

2. direction of shifting

3. character of shifting (simple or cyclic)

4. on the amount of bits, on which an operand is shifted after operation implementation.

An instruction format contains three fields at least.

Logical shift is the shift of operand numerical code without the account of its numerical equivalent.

Arithmetical shift is a shift of operand numerical code taking into account its numerical equivalent.

In this case if for the numerical values presentation are not used the special formed codes (it means that data is unsigned), then it is not distinctions between logical and arithmetical shifts. If for the presentation of numerical values taking into account a sign, the special codes (direct, indirect, additional) are used, an arithmetic shift on principle differs from procedure of logical shift.

Example:

1. Logical shift.

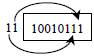
Е5 = 11100101 АСС:=L2(АСС) result: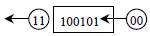

Exact record: АСС:=L2(АСС(5:0)).00 Right change like.

Circular shift on 2 bits: АСС:=L2(АСС(5:0)).АСС(7:6)

2. Arithmetical shift.

Shift of number to the left and to the right corresponds to dividing or multiplication of number by radix of CC.

11100101 binary code of number –27.

At an arithmetic shift to the left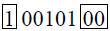

At the shift to the right: 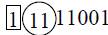in an additional code.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.