• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Про єдиний закон збереження маси, імпульсу і енергії

За виразом 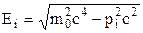знайдемо власну масу якоїсь 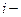тої частинки

. (1.92)

Поширимо цей вираз на ізольовану систему невзаємодіючих частинок. Енергія і імпульс системи дорівнюють відповідно

; ,

де 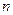– кількість частинок у системі.

Підставивши ці величини у вираз (1.92), знайдемо власну масу системи

.

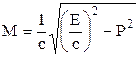Для ізольованої системи справджується закон збереження імпульсу та закон збереження енергії

; ,

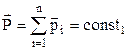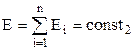то відповідно буде зберігатись також власна маса системи

. (1.93)

У релятивістській механіці рівняння (1.93) виражає зміст закон збереження маси, імпульсу і енергії. У класичній механіці, як відомо, розглядаються три окремі закони збереження маси, імпульсу і енергії.

На закінчення повернемось до сил інерції, які діють в неінерціальних системах відліку. Характерною властивістю сил інерції є те, що вони пропорційні масам тіл 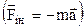. Тому в полі сил інерції усі тіла рухаються з одним і тим же прискоренням. Таку ж властивість мають і сили тяжіння .

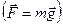Із аналізу явищ в неінерціальних системах відліку Ейнштейн вивів положення, яке отримало назву принципу еквівалентності сил інерції і сил тяжіння.

Слід зауважити, що це положення не відносить сили тяжіння до розряду фіктивних. Згадаємо, що сили інерції є фіктивними. Тут мова йде лише про те, що властивості простору і часу і в полі сил інерції і в полі сил тяжіння однакові.

Принцип еквівалентності сил інерції і сил тяжіння позволив перейти до розгляду неінерціальних систем відліку, тобто до створення загальної теорії відносності або точніше релятивістської теорії тяжіння.

Читайте також:

1. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
2. III. За виділенням або поглинанням енергії
3. IV. Закони ідеальних газів.
4. IV. Закономірності структурно-функціональної організації спинного мозку
5. IV. Критерій питомої потенціальної енергії деформації формозміни
6. Авілум – “син чоловіка” – повноправна людина, охороні його життя, здоров’я, захисту його майнових інтересів присвячена значна частина законника.
7. Аграрне право та законодавство США, Німеччини, Франції, Великої Британії, Ізраїлю, Польщі, Росії
8. Аграрні закони України
9. Адаптація законодавства України до законодавства ЄС - один із важливих інструментів створення в Україні нової правової системи та громадянського суспільства
10. Адаптація законодавства України до законодавства ЄС - один із важливих інструментів створення в Україні нової правової системи та громадянського суспільства
11. Адміністративна відповідальність за порушення аграрного законодавства
12. Адміністративна відповідальність за порушення земельного законодавства

Переглядів: 876