• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Закон взаємозв’язку між масою і енергією

Помножимо основне рівняння динаміки (1.86) скалярно на вектор елементарного переміщення

,

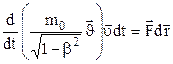(в лівій частині рівняння враховано, що ).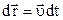

Проведемо інтегрування цього рівняння вздовж траєкторії, наприклад, від точки 1 до точки 2

.

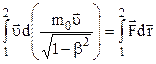Зауважимо, що інтеграл справа дає роботу і перетворимо підінтегральний вираз зліва до іншого вигляду

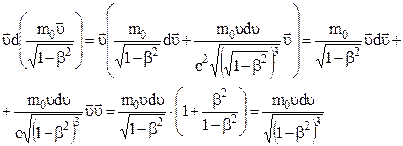(1.89)

(в ході перетворень бралось до уваги, що ; ).

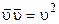Тепер продиференціюємо вираз для маси

або 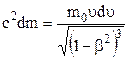. (1.90)

Порівнюючи формули (1.89) і (1.90), бачимо, що підінтегральний вираз зліва дорівнює .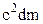

Отже,

.

Звідки .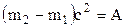

За загальним законом збереження і перетворення енергії

.

Тоді

.

Легко переконатись способом підстановки, що останнє рівняння перетворюється в тотожність при

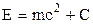, де 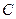– довільна стала величина.

Покладемо тимчасово, що 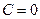і перетворимо формулу до іншого вигляду:

.

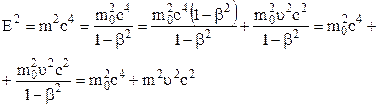Зауваживши, що величина дає релятивістський імпульс , маємо

або

(отримані формули виражають зв’язок між енергією 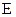і імпульсом 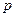в релятивістській механіці).

Тепер запишемо першу формулу дещо по-іншому

.

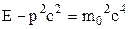Права частина цього виразу є інваріантною величиною, тобто однаковою в усіх інерціальних системах відліку. Отже, і ліва частина має бути інваріантною. Експериментальні дослідження над швидкими частинками підтвердили інваріантність згаданого виразу. І тому відповідно до досліду константу інтегрування 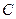мусимо брати рівною нулю.

Таким чином,

або . (1.91)

Якщо тіло нерухоме , то 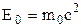. Бачимо, що енергія 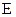не зводиться до кінетичної і тому її називають повною або релятивістською енергією. Енергію 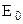називають енергією спокою тіла; вона є внутрішньою енергією тіла.

Рівняння (1.91) виражає один із фундаментальних законів природи – закон взаємозв’язку маси і енергії: повна енергія тіла дорівнює добутку релятивістської маси тіла на квадрат швидкості світла у вакуумі.

Зауважимо, що експериментальні підтвердження закону взаємозв’язку маси і енергії дають ядерні реакції. Характерним наслідком їх є так званий дефект маси 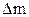(див. розділ “Ядерна фізика”).

Кінетичну енергію в релятивістській механіці визначають як різницю 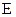і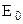

.

У випадку малих швидкостей цю формулу можна перетворити таким чином:

,

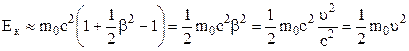тобто ми приходимо до класичного виразу кінетичної енергії.

Читайте також:

1. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
2. IV. Закони ідеальних газів.
3. IV. Закономірності структурно-функціональної організації спинного мозку
4. Авілум – “син чоловіка” – повноправна людина, охороні його життя, здоров’я, захисту його майнових інтересів присвячена значна частина законника.
5. Аграрне право та законодавство США, Німеччини, Франції, Великої Британії, Ізраїлю, Польщі, Росії
6. Аграрні закони України
7. Адаптація законодавства України до законодавства ЄС - один із важливих інструментів створення в Україні нової правової системи та громадянського суспільства
8. Адаптація законодавства України до законодавства ЄС - один із важливих інструментів створення в Україні нової правової системи та громадянського суспільства
9. Адміністративна відповідальність за порушення аграрного законодавства
10. Адміністративна відповідальність за порушення земельного законодавства
11. Адміністративна відповідальність за порушення податкового законодавства.
12. Адміністративна відповідальність осіб, винних в порушенні податкового законодавства

Переглядів: 601