• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

ЗАСТОСУВАННЯ ТЕОРЕМИ ОСТРОГРАДСЬКОГО - ГАУССА

Теорема дає можливість визначити напруженість електричних полів навколо заряджених тіл з симетричним розподілом їх зарядів і діелектриків, що оточують їх. Розглянемо найтиповіші приклади.

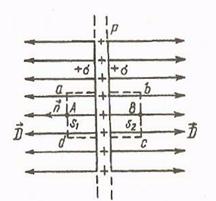
Рис. 1.4. Визначення напруженості поля площини

1. Напруженість електричного поля рівномірно зарядженої нескін­ченної площини. Під рівномірно зарядженою розуміють площину з сталою поверхневою густиною заряду

. (1.11)

Щоб визначити напруженість електрич­ного поля в якійсь точці А (рис. 1.4), вибе­ремо симетричну їй точку В і побудуємо допоміжний циліндр abcd так, щоб його твір­на була паралельна лініям індукції, а основи S₁=S₂=S проходили через вибрані точки і були паралельні площині Р. Потік індукції через бічну поверхню циліндра дорівнює ну­лю, а через основи:

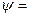DS₁+DS₂=2DS. (1.12)

За теоремою Остроградського - Гаусса:

. (1.13)

Прирівнявши праві частини рівнянь (1.12) і (1.13), дістанемо:

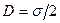. (1.14)

Оскільки , то у випадку однорідного середовища ():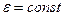

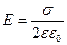. (1.15)
Таке поле однорідне, симетричне, і його напруженість не залежить від положення точки (точку А взято довільно).

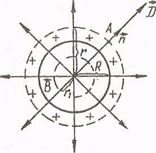
2. Напруженість електричного поля рівномірно зарядженої сферичної поверхні.

Рис. 1.5. Визначення напруженості поля сфери

Нехай сферична поверх­ня, радіус якої R, заряджена рівномірно (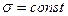). Тоді електричне поле буде си­метричним відносно центра, а вектори ін­дукції будуть напрямлені радіально від поверхні, якщо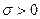, і до поверхні, якщо 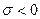(рис. 1.5). Вектор зовнішньої нормалі 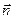також радіальний, тому .

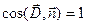Визначимо напруженість електричного поля в точці А на відстані r > R від центра сфери. Для цього проведемо через точку А допоміжну концентричну сферу радіусом r. Для всіх точок цієї сфери 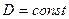. Потік індукції через допоміжну поверхню .буде:

. (1.16)

За теоремою Остроградського—Гаусса цей потік визначають так:

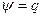, (1.17)

де q - повний заряд сфери. З рівнянь (1.16) і (1.17) дістаємо:

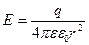, (1.18)

Як бачимо, електричне поле поза рівномірно зарядженою сферою таке саме (еквівалентне), як і поле точкового зарядженого тіла, коли його заряд дорівнює всьому зарядові сфери.

1.4. ПОТЕНЦІАЛ. РОБОТА ПОЛЯ. НАПРУГА

План лекції

1.4.1. Робота сил електричного поля. Потенціальний характер електричного поля

1.4.2. Потенціал електричного поля

1.4.3. Різниця потенціалів (напруга). Еквіпотенціальні поверхні

1.4.1. РОБОТА СИЛ ЕЛЕКТРИЧНОГО ПОЛЯ. ПОТЕНЦІАЛЬНИЙ ХАРАКТЕР ЕЛЕКТРИЧНОГО ПОЛЯ

Відомо, що на точкове заряджене тіло з зарядом q₀, внесене в електричне поле, діятиме сила F=Eq₀. Під дією цієї сили тіло може переміщуватися і тоді над ним виконуватиметься робота. Якщо поле неоднорідне, то діюча сила змінюватиметься, бо вектор напруженості в різних точках поля має різні напрям і величину. Тому на елементарному переміщенні зарядженого тіла dl роботу знайдемо за виразом

dA = Fdl 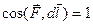= q₀Edl q₀ E_l, dl, (1.19)

де Е_l - складова вектора напруженості в напрямі переміщення. Якщо тіло переміщується з якоїсь точки поля 1 в довільну точку 2, то робота визначиться сумою елементарних робіт, тобто інтегралом

(1.20)

Рис. 1.6. Визначення роботи сил електричного поля

Для прикладу визначимо роботу сил електричного поля, пов'язаного з точковим позитивно зарядженим тілом. З рис. 1.6 видно, що:

dldr.

Напруженість розглядуваного поля має значення :

,

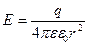тому за виразом (1.20) дістанемо

, (1.21)

де r₁ і r_{2 -} відстані точок 1 і 2 від нерухомого зарядженого тіла.

З виразу (1.21) випливає, що при різних переміщеннях точкового зарядженого тіла робота сил електричного поля не залежить від форми шляху руху точки, а залежить лише від початкового і кінцевого її положень, діелектричних властивостей середовища і заряду точки. Цей висновок відповідно до принципу суперпозиції поширюється на електричне поле, пов'язане з будь-якою системою заряджених тіл.

Поля, робота в яких не залежить від форми шляху, називаються потенціальними. Отже електростатичне поле потенціальне.

1.4.2. ПОТЕНЦІАЛ ЕЛЕКТРИЧНОГО ПОЛЯ. РІЗНИЦЯ ПОТЕНЦІАЛІВ (НАПРУГА). ЕКВІПОТЕНЦІАЛЬНІ ПОВЕРХНІ

За законом збереження і перетворення енергії при переміщенні заряду q₀ робота сил електричного поля дорівнює зменшенню потенціальної енергії цього заряду в силовому полі, тобто dA = - dW_p, або:

, (1.22)

де q_{0 -} заряд переміщуваного тіла. Розглянемо два випадки застосування рівняння (1.22).

1. Нехай пробне тіло переміщується в електричному полі з будь-якої точки 1 на нескінченність, тоді (1.22) запишемо так:

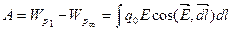, (1.23)

де W_P1 і W_P∞ - потенціальні енергії пробного тіла із зарядом у точці поля 1 і в нескінченності.

При переміщенні в нескінченність сили поля зменшуються і потенціальна енергія тіла прямує до нуля, тому можна вважати, що в нескінченності вона дорівнює нулю, тобто W_P∞ = 0. Тоді:

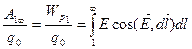. (1.24)

Отже, робота, визначена на одиницю заряду пробного тіла, при переміщенні його з нескінченності в задану точку поля 1 не залежить від форми шляху, величини пробного заряду, а залежить від властивостей наявного електричного поля. Тому ця робота може бути енергетичною характеристикою електричного поля в заданій точці. Цю роботу позначають через φ і називають потенціалом електричного поля в заданій точці,тобто:

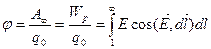. (1.25)

Потенціалом електричного поля в заданій точці називається фізична величина, що чисельно дорівнює роботі, яку виконують сили електричного поля при переміщенні пробного тіла з одиничним позитивним зарядом із заданої точки у нескінченність (або в точку поля, для якої умовно прийнято, що потенціал дорівнює нулю); інакше, потенціалом φ у заданій точці електричного поля називається фізична величина, що чисельно дорівнює потенціальній енергії пробного точкового тіла з одиничним позитивним зарядом, вміщеним у дану точку поля.

Потенціал, як і напруженість, стосується певної точки поля. Ці величини відмінні за змістом. Вони дають змогу різними методами оцінити електричне поле з кількісного боку. Напруженість є силова, векторна характеристика поля. Потенціал є скалярною, енергетичною характеристикою електричного поля. Одиниця потенціалу в СІ

1 В = 1Дж/Кл.

Для прикладу знайдемо вираз для потенціалу електричного поля, пов'язаного з точковим зарядженим тілом, у точці на відстані r від нього. Користуючись рівнянням (1.25) і враховуючи, що:

dldr,

дістанемо:

dr, (1.26)

де q - заряд точкового тіла.

1.4.3. РІЗНИЦЯ ПОТЕНЦІАЛІВ (НАПРУГА). ЕКВІПОТЕНЦІАЛЬНІ ПОВЕРХНІ

Зауважимо, що практичне значення має (для обчислення роботи поля) не потенціал, а різниця потенціалів; тому за нульове значення потенціалу можна взяти потенціал будь-якого тіла, наприклад, за нульовий беруть потенціал Землі.

Розглянемо випадок, коли пробне тіло з зарядом q₀ переміщується в електричному полі з точки 1 в точку 2. Тоді з виразу (1.26) знайдемо:

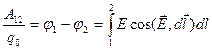, (1.27)

де φ₁ - φ₂ = U_{12 -} напруга.

Напруга між двома точками електричного поля дорівнює різниці потенціалів у цих точках і вимірюється роботою, яку виконують сили електричного поля, переміщуючи пробне тіло з одиничним зарядом з однієї точки поля в другу. Вимірюють напругу в СІ у вольтах.

З виразу (1.27) знаходимо:

. (1.28)

Робота електричного поля при переміщенні точкового зарядженого тіла з однієї точки в іншу чисельно дорівнює добутку заряду тіла на напругу між цими точками.

Якщо заряджене тіло переміщується по замкнутому контуру (φ₁ - φ₂), то робота сил електричного поля дорівнює нулю. Звичайно, робота дорівнюватиме також нулю, коли заряджене тіло переміщуватиметься між точками поля, потенціали яких однакові.

Геометричне місце точок поля, потенціали яких однакові, називається еквіпотенціальною поверхнею, або поверхнею однакового потенціалу (φ = const).

Для еквіпотенціальної поверхні:

,

звідки

0,

а отже, тобто лінії напруженості перпендикулярні до еквіпотенціальних поверхонь. Еквіпотенціальні поверхні поля зарядженого точкового тіла мають вигляд концентричних сфер, у центрі яких міститься тіло. Для однорідного поля еквіпотенціальні поверхні є паралельними площинами.

Отже, електричне поле можна охарактеризувати векторною величиною - напруженістю E і скалярною величиною - потенціалом φ.

Встановимо зв’язок між напруженістю і напругою. За формулою (1.28) А = qU. Цю роботу можна виразити як добуток електричної сили на шлях l:

A=Fl=qEl.

Прирівнявши праві частини цих формул, отримаємо:

E=U/l . (1.29)

З виразу (1.29) випливає, що одиницею напруженості в СІ є 1 В/м.

Електричне поле можна графічно зображати не тільки лініями напруженості, а й за допомогою еквіпотенціальних поверхонь. Зручно проводити їх так, щоб потенціали двох суміжних еквіпотенціальних поверхонь відрізнялися на однакову величину (наприклад, ∆φ= 1 В).

1.5. ПРОВІДНИКИ І ДІЕЛЕКТРИКИ В ЕЛЕКТРИЧНОМУ ПОЛІ

План лекції

1.5.1. Провідники в електричному полі. Електростатична індукція

1.5.2. Діелектрики в електричному полі. Поляризація діелектрика

1.5.3. Особливості деяких діелектриків

1.5.1. ПРОВІДНИКИ В ЕЛЕКТРИЧНОМУ ПОЛІ. ЕЛЕКТРОСТАТИЧНА ІНДУКЦІЯ

У металевих провідниках завжди є вільні електрони. Це пояснюється тим, що в металах валентні електрони слабко пов'язані з позитивно зарядженими ядрами атомів і легко відділяються від атомів. Якщо металевий провідник внести в електричне поле, то

під впливом електричних сил вільні електрони перерозподіляться: частина їх зміститься в протилежному до вектора напруженості 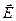зовнішнього електричного поля напрямі (область А) а на іншому боці провідника внаслідок цього не вистачатиме електронів і буде надлишок позитивних зарядів (область В). У провіднику виникає наведене електричне поле, вектор напруженості якого 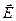напрямлений протилежно до вектора напруженості ) навідного поля (явище електростатичної індукції).

Рис. 1.7. Електростатична індукція

Перерозподіл зарядів триватиме доти, поки напруженість поля всередині провідника не дорівнюватиме нулю, а поверхня провідника стане еквіпотенціальною - лінії напруженості зовнішнього поля будуть перпендикулярними до поверхні провідника (рис. 1.7).

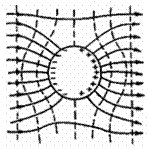
Рис. 1.8. Лінії напруженості електричного поля біля провідника

Описане явище називають електростатичною індукцією. Воно веде до того, що внесений в електричне поле провідник деформує дане поле; одна частина ліній напруженості розривається провідником, а решта ліній вигинається в бік провідника. Оскільки тепер всередині провідника електричного поля немає, то картини деформованого поля будуть однакові й для суцільного, і для порожнистого провідників.

Якщо в порожнистий провідник внести яке-небудь тіло, то на нього не діятиме зовнішнє електричне поле. Це явище використовується для екранізації (електростатичного захисту) чутливих приладів і вузлів машин.

1.5.2. ДІЕЛЕКТРИКИ В ЕЛЕКТРИЧНОМУ ПОЛІ. ПОЛЯРИЗАЦІЯ ДІЕЛЕКТРИКІВ

Діелектриками називають речовини, в яких за нормальних умов (без дії зовнішніх агентів і при не дуже високій температурі) немає вільних електричних заряджених частинок.Позитивні й негативні мікроскопічні частинки в рівних кількостях зв'язані з атомами і молекулами діелектрика. Тому атоми і молекули діелектрика в цілому нейтральні. Але це не означає, що зовнішнє електричне поле не впливає на діелектрик.

Рис. 1.9. Диполі всередині діелектрика

Під впливом сил поля зв'язані заряджені частинки можуть зміщуватися в межах мікроскопічних об'ємів.

Процес зміщення зв'язаних заряджених частинок діелектрика під впливом зовнішнього електричного поля називається поляризацією діелектрика.

Розглянемо процес поляризації з молекулярної точки зору. Молекули тіл - це електродинамічні системи, які складаються з позитивних ядер і негативних орбітальних електронів. Тому можна говорити про центри позитивних і негативних зарядів молекул і всі діелектрики поділити на такі три групи.

До першої групи можна віднести діелектрики, в молекулах яких центри позитивних і негативних зарядів не збігаються (рис. 1.10) Молекули таких діелектриків мають асиметричну будову; в них виражені полюси позитивних і негативних зарядів. Такі молекули називаються полярними. Електричне поле полярної молекули в першому наближенні можна уподібнити до поля деякого еквівалентного електричного диполя із сталим дипольним моментом:

, (1.30)

де l - відстань між електричними центрами.

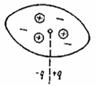
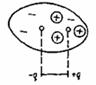
Рис. 1.10. Полярна молекула Рис. 1.11. Неполярна молекула

До діелектриків з полярними молекулами належать: Н₂О, NO₂, SO₂, NH₃, HC1, СНСl, органічні кислоти та інші речовини.

До другої групи можна віднести діелектрики, в молекулах яких центри позитивних і негативних частинок збігаються (рис. 1.11). Молекули таких діелектриків називаються неполярними. Зокрема, до діелектриків цієї групи належать: Н₂, N₂, СО₂, ССl₄, парафін, бензол та ряд інших вуглеводнів.

До третьої групи діелектриків належать іонні кристали, в просторових решітках яких правильно чергуються позитивні й негативи іони (наприклад, NaCl, KC1, CsCl). У таких кристалах не можна виділити окремих молекул, і їх можна розглядати як сукупність дво: іонних решіток, вставлених одна в одну.

Для кількісної оцінки поляризації діелектрика вводиться поняття вектора поляризації 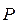. Під вектором поляризації розуміють векторну суму електричних дипольних моментів молекул одиниці об'єму поляризованого діелектрика; інакше, вектор поляризації визначається електричним дипольним моментом одиниці об'єму поляризованого діелектрика. За означенням вектор поляризації дорівнює:

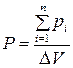, (1.31)

де P_i - електричний момент і-го диполя; n - кількість диполів в об'ємі ∆V.

. (1.32)

Отже, кількісною характеристикою електричних властивостей діелектрика є безрозмірна величина є - відносна діелектрична проникність діелектрика.

1.5.3. ОСОБЛИВОСТІ ДЕЯКИХ ДІЕЛЕКТРИКІВ

Серед діелектриків трапляються такі, які мають дуже великі значення відносної діелектричної проникності, їх називають сегнетоелектриками.Таку назву вони дістали від типового представника цієї групи - сегнетової солі (подвійна натрієво-калієва сіль винної кислоти NaKC₄Н₄О₃₆•4Н₂О). При кімнатній температурі відносна діелектрична проникність її досягає 10000. До сегнетоелектриків належить також титанат барію ВаТіО₃ (e = 6000), титанат свинцю РbТіО₃, ніобат літію LiNbO тощо.

Висока діелектрична проникність сегнетоелектриків пов'язана з наявністю в них самодовільних (спонтанних) поляризованих областей без впливу зовнішнього поля. Ці області спонтанної поляризації називають доменами.

Рис. 1.12. Домени

У сусідніх доменах орієнтація дипольних моментів інша (рис. 1.12). Тому вектор поляризації досить великого монокристала дорівнює нулю і в цілому сегнетоелектрик неполяризований. Але якщо його внести в електричне поле, то вектори поляризації доменів встановлюються в напрямі, близькому до напряму поля, і тим більше, чим сильніше діє поле; сегнетоелектрик поляризується, і відносна діелектрична проникність набуває великого значення.

Висока діелектрична проникність сегнетоелектриків виявляється в цілком певних температурних інтервалах. Для кожного з них існує така температура, вище (і нижче) від якої сегнетоелектричні властивості істотно ослаблюються. Цю температуру називають точкою Кюрі.

Коли температура сегнетоелектрика досягає значення точки Кюрі, зростає тепловий рух частинок і порушується орієнтація дипольних моментів в областях спонтанної поляризації - домени руйнуються, і сегнетоелектрик перетворюється в звичайний діелектрик.

Для сегнетоелектриків існує специфічна залежність вектора поляризації від напруженості зовнішнього електричного поля 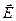, що дістала назву діелектричного гістерезису (запізнення) ( рис. 1.13).

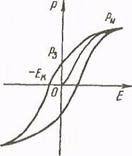
Рис. 1.13. Діелектричний гістерезис

Спочатку із збільшенням напруженості зовнішнього поля вектор поляризації швидко зростає, настає стан насичення (крива ОP_н). Якщо ж після цього напруженість електричного поля зменшувати і довести до нуля, то поляризація зменшується з запізненням і досягає деякого залишкового значення P₃ (крива P_нP_з). Залишкова поляризація зникає лише при накладанні певного електричного поля протилежного напряму -Е_к. Напруженість Е_к поля, при якій усувається залишкова поляризація даного діелектрика, називається його коерцитивною силою.

Сегнетоелектрики широко використовуються у конденсаторах, у запам'ятовуючих пристроях електронно-обчислювальних машин тощо.

Є чимало таких діелектриків, які довгий час зберігають стан поляризації, - від кількох днів до багатьох років, їх називають електретами.

Для одержання електретів використовують органічні (віск, парафін, нафталін, ебоніт, слюду та ін.) і неорганічні (сірку, титанати лужноземельних металів - СаТіО3, SrTiO3 і ін.) діелектрики та їх суміші. Виготовляють їх нагріванням до температури плавлення з наступним охолодженням у сильному електричному полі.

Усі електрети мають стабільний поверхневий заряд (не більший за густиною

σ =10^-4 Кл/м²). Цей заряд звичайно вимірюють за допомогою електричної індукції. Електрет є аналогом постійного магніту. Використовують електрети як джерела постійного електричного поля в схемах телефонного зв'язку, електрометрах, у дозиметричних радіаційних приладах тощо.

1.6. ЕЛЕКТРОЄМНСЬ. КОНДЕНСАТОРИ. З'ЄДНАННЯ КОНДЕНСАТОРІВ

План лекції

1.6.1. Електроємність провідника

1.6.2. Конденсатори та їх застосування

1.6.3. З’єднання конденсаторів

1.6.1. ЕЛЕКТРОЄМНІСТЬ ПРОВІДНИКА

Нехай маємо наелектризований відокремлений провідник в однорідному середовищі. Заряд q розподілиться на його поверхні певним способом і вона в усіх точках набуде деякого потенціалу φ. Якщо заряд на провіднику збільшити в n раз, то й потенціал у кожній точці поверхні його збільшиться в стільки ж разів. Дослідами встановлено, що відношення величини заряду q провідника до відповідного значення потенціалу φ в точках його поверхні є сталим:

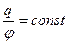
Це відношення називають електроємністю відокремленого провідника (або просто ємністю):

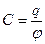. (1.33)

Електроємність залежить від геометричних розмірів і форми провідника, розташування навколо нього інших провідників, діелектричних властивостей середовища. Електроємність не залежить від матеріалу провідника, наявності в ньому порожнин та від величини заряду.

За одиницю електроємності в СІ прийнято електроємність такого відокремленого провідника, із зміною заряду якого на один кулон потенціал точок його поверхні змінюється на один вольт. Ця одиниця дістала назву фарада (Ф): 1 Ф = 1 Кл/В.

1.6.2. КОНДЕНСАТОРИ ТА ЇХ ЗАСТОСУВАННЯ

Конденсатор складається з двох провідників - обкладок, відокремлених прошарком діелектрика. Наближаючи обкладки і розміщуючи між ними ізоляційний прошарок з високою діелектричною проникністю можна створити конденсатори великої ємності. Такий конденсатор дає можливість нагромаджувати на обкладках великі заряди при невисоких напругах і малих розмірах приладу. Зазначимо, що електричне поле конденсатора майже повністю локалізоване у вузькому зазорі між його обкладками і тому на нього не впливають навколишні тіла. Ємність конденсатора не змінюється. Його обкладки мають заради однакової величини, але протилежні за знаком.

Як показують досліди, відношення абсолютної величини заряду до різниці потенціалів обкладок залишається сталим:

.

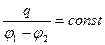Це відношення називається взаємною електроємністю або просто ємністю конденсатора, тобто:

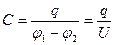. (1.34)

Електроємність конденсатора залежить від форми обкладок, їх розмірів, розміщення і діелектричних властивостей середовища між ними. Залежно від форми обкладок конденсатори бувають плоскі, циліндричні, сферичні.

Конденсатори широко використовують в електротехнічних і радіотехнічних схемах.

За будовою і типом діелектриків між провідниками розрізняють повітряні, керамічні, слюдяні, паперові, електролітичні конденсатори, конденсатори постійної і змінної ємності.

1.6.3. З’ЄДНАННЯ КОНДЕНСАТОРІВ

Кожний конденсатор характеризується, крім ємності, також пробивною та робочою напругою. Тому, щоб дістати потрібну ємність при даній робочій напрузі, доводиться конденсатори з'єднувати в батарею - паралельно, послідовно або мішано.

Паралельне з'єднання застосовують для того, щоб дістати більшу ємність, ніж ємність одного конденсатора. Обкладки конденсаторів з'єднують у дві групи, потенціали яких φ₁ і φ₂ (рис. 1.14). Тому напруга φ₁ - φ₂ = U залишається спільною для всіх конденсаторів, а заряди різні, q_і = С_іU, де Сі - ємність і-го конденсатора. Заряд батареї:

,

звідки

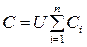, (1.35)

де n - кількість конденсаторів у батареї. Збільшення електроємності при паралельному з'єднанні конденсаторів пояснюється тим, що збільшується робоча поверхня S обкладок.

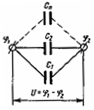
Рис. 1.14. Паралельне з'єднання конденсаторів

При послідовному з'єднанні обкладки окремих конденсаторів мають заряди, чисельно однакові, але протилежні за знаком (рис. 1.15). Напруга на і-му конденсаторі: .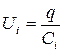

Тоді загальна напруга батареї:

,

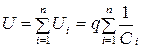звідки:

. (1.36)

Рис. 1.15. Послідовне з'єднання конденсаторів

У цьому з'єднанні ємність батареї менша від ємностей окремих конденсаторів (С < С_і). Це пояснюється тим, що проміжні обкладки в батареї не відіграють суттєвої ролі, діють тільки крайні обкладки, відстань між якими збільшилась. Напруга на кожному конденсаторі (і можливість пробою) зменшується. Коли є потреба збільшити електроємність батареї, то з'єднують паралельно окремі групи послідовно з'єднаних конденсаторів (мішане з'єднання).

ПИТАННЯ ДЛЯ САМОСТІЙНОГО ОПРАЦЮВАННЯ

1. Система СГСЕ

2. Теорія близькодії і далекодії

3. Поле системи зарядів

4. Основні поняття векторного аналізу

5. Властивості векторних полів

6. Встановлення зв’язку між напруженістю електричного поля і потенціалом на основі векторного аналізу

7. Поле диполя

8. Енергія взаємодії системи зарядів

9. Тензор діелектричної сприйнятливості

10. Об’ємні і поверхневі зв’язані заряди

11. Умови на межі двох діелектриків

12. Обчислення поля в діелектриках

13. Ємність сферичного конденсатора

14. Ємність циліндричного конденсатора

15. Енергія конденсатора

ПИТАННЯ ДЛЯ САМОПЕРЕВІРКИ ЗНАНЬ

1. Що таке електростатика?

2. Чим зумовлена електризація тіл?

3. Що таке електричний заряд?

4. Що таке елементарний заряд?

5. Сформулюйте закон збереження електричного заряду

6. Що таке анігіляція?

7. Що таке інваріантність?

8. Що таке точковий заряд?

9. Сформулюйте закон Кулона для точкових електричних зарядів. (Записати формулу)

10. Показати на малюнку напрям сили взаємодії двох однойменних зарядів, двох різнойменних зарядів)

11. Що таке електричне поле?

12. Що таке електростатичне поле?

13. Назвіть основні характеристики електростатичного поля.

14. Основна властивість електричного поля?

15. Що називають напруженістю електричного поля (записати формулу)?

16. Записати формулу напруженості поля точкового заряду

17. Що таке силові лінії? (Зобразити силові лінії точкового позитивного, точкового негативного зарядів та рівномірно зарядженої площини)

18. Що таке однорідне поле? (Зобразити його)

19. Принцип суперпозиції полів

20. Сформулюйте визначення потенціалу точки електричного поля

21. Записати формулу потенціалу поля точкового заряду

22. Що таке напруга (записати формулу)?

23. Які поля називають потенціальними?

24. Що таке еквіпотенціальна поверхня? (Зобразити еквіпотенціальні поверхні точкового позитивного, точкового негативного зарядів та рівномірно зарядженої площини)

25. Чому дорівнює робота з переміщення електричного заряду вздовж еквіпотенціальної поверхні?

26. Яким співвідношенням зв'язані між собою напруженість і потенціал електричного поля?

27. Що таке діелектрична проникність?

28. Яке практичне застосування має теорема Гаусса?

29. Сформулювати теорему Гаусса (записати формулу)

30. Що таке електростатична індукція? (У яких речовин вона буває?)

31. Описати стан провідника в електричному полі

32. Що таке екранізація?

33. Чи є всередині провідників електричне поле? Чому?

34. Чим метали відрізняються від діелектриків?

35. Що таке диполь?

36. Що таке полярний діелектрик (приклади)?

37. Що таке неполярний діелектрик (приклади)?

38. Що таке поляризація?

39. Що таке сегнетоелектрики?

40. Що таке гістерезис? (Зобразити його)

41. Що таке електрети?

42. Чи є всередині діелектрика електричне поле? Чому?

43. Описати стан діелектрика в електричному полі

44. Що таке електроємність?

45. Що таке конденсатор?

46. Формула ємності плоского конденсатора.

47. Типи конденсаторів

48. Закони послідовного з’єднання конденсаторів (рисунок і формули)

49. Закони паралельного з’єднання конденсаторів (рисунок і формули)

Читайте також:

1. V. Виконання вправ на застосування узагальнювальних правил.
2. А.1 Стан , та проблемні питання застосування симетричної та асиметричної криптографії.
3. Автомобільні ваги із застосуванням цифрових датчиків
4. Аксіоми. Теореми. Ознаки.
5. Акти застосування норм права в механізмі правового регулювання.
6. Акти застосування юридичних норм: поняття, ознаки, види.
7. Акти правозастосування, їх види
8. Акти правозастосування.
9. Алгоритм із застосування річної процентної ставки r.
10. Алгоритм із застосуванням річної облікової ставки d.
11. Аміноглікозиди (стрептоміцину сульфат, гентаміцину сульфат). Механізм і спектр протимікробної дії, застосування, побічні ефекти.
12. Аналіз зображувальних засобів. Застосування цілісного аналізу

Переглядів: 6718