
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Шифр зсуву.
Афінні шифри
В цьому параграфі ми розглянемо афінні шифри — підклас шифрів заміни, що включає як частковий випадок шифр Віженера і навіть шифр перестановки з фіксованим періодом.
3.1. Шифри простої заміни II. Зазначимо, що в рамках формалізації, впровадженої у пункті 1.1, моноалфавітні k-грамні шифри заміни можна означити як блокові шифри з періодом k. Відповіднo шифри простої заміни можна трактувати як блокові шифри з перідом l.
Давайте повернемось ще раз до шифру зсуву, нашого першого прикладу шифру простої заміни (пункти 1.1.1 та 1.2.1). Подивимось, як можна описати цей шифр із застосуванням арифметичного апарату розвиненого у попередньому параграфі. Користь такого підходу зрoзуміла — обчислювальну техніку майже завжди простіше навчити оперувати із числовою інформацією, аніж із символьною. Основна домвленість, якої ми будемо дотримуватись до кінця цього параграфу, тaка:
| n-символьний алфавіт утотожнюємо з кільцем Zn. А саме, кожна буква замінюється чвоїм номером у алфавіті причому номерація починається з нулч |
Наприклад, латинська абетка утотожнюється із Z26, а українська із Z33. Літера а української абетки трактується як 0, літера б як 1, в як 2 і т.д. Тепер до букв відкритого тексту ми можемо вільно застосовувати • операції додавання та множення за відповідним модулем.
До кінця параграфу n буде служити позначенням для кількості букв у алфавіті відкритого тексту. Отже:
Ключ: s таке, що 0  s < п.
s < п.
Шифрування. У повідомленні кожна буква х заміщується буквою; Е(х) = (х + s) mod n.
Дешифрування. У криптотексті кожна буква х' заміщується буквою D(x') = (х' + s') mod п, де s' = п - s. Величину зворотнього зсуву s' будемо називати дешифруючим ключем.
За аналогією введемо у розгляд
ЛІНІЙНИЙ ШИФР.
Ключ: а таке, що 0  а < п і НСД (а, п) = 1.
а < п і НСД (а, п) = 1.
Шифрування.У повідомлені кожна буква х заміщується буквою У(х) = (ах)modn
Дешифрування. У криптотексті кожна буква х' заміщується буквою
D(x') = (а'х' + s') mod n, де пара а' = a-1 mod n дешифруючий ключ.
3.2. Афінні шифри вищих порядків. Подумаємо, як можна розширити монограмні шифри попереднього пункту так, щоб вони оперували з k-грамами для довільного k > 1. Спочатку введемо операцію додавання в 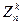 . Сумою векторів X = (х1,..., xk) і S = (s1,..., Sk) з
. Сумою векторів X = (х1,..., xk) і S = (s1,..., Sk) з 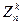 є вектрр X + S = (х1 + s1) mod n,..., (xk + sk) mod n).
є вектрр X + S = (х1 + s1) mod n,..., (xk + sk) mod n). 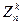 з операцією додавання є групою. Вектор —S = (п – s1,.. ., n — sk) є оберненим до вектора S — (s1,..., sk).
з операцією додавання є групою. Вектор —S = (п – s1,.. ., n — sk) є оберненим до вектора S — (s1,..., sk).
ШИФР ЗСУВУ К-ГО ПОРЯДКУ (ШИФР ВІЖЕНЕРА З ПЕРІОДОМ k).
Ключ: S Є 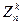 .
.
Шифрування. Повідомлення розбивається на k-грами. Кожна k-грама X заміщується
k-грамою Е(Х) = X + S.
Дешифрування. Кожна k-грама X’ криптотексту заміщується k-грамою D(X') = X’ + S', де S' = —S є дешифруючим ключем.
Перед тим як перейти до лінійного шифру нагадаємо, що через Mk(Zn) ми позначаємо множину матриць розміру А х А; з коефіцієнтами з кільця Zn, а через GL(Zn) — підмножину оборотних матриць. Для А Є GLk(Zn) обернену до неї матрицю позначаємо через А-1 Добутком АХ матриці А = (aij) з Mk(Zn) на вектор-стовпчик X = (х1,..., xk) з 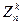 є вектор-стовпчик
є вектор-стовпчик
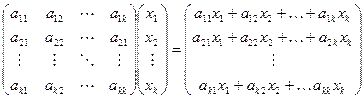
ЛІНІЙНИЙ ШИФР К-ГО ПОРЯДКУ.
Ключ: A GLk(Zn).
GLk(Zn).
Шифрування. Повідомлення розбивається на k-грами. Кожна k- грама X заміщується
k-грамою Е(Х) = АХ.
Дешифрування. Кожна k-грама X’ криптотексту заміщується k-грамою D(X') = А'Х', де А' = А-1 — дешифруючий ключ.
Приклад 3.4. Лінійний шифр 1-го порядку обговорювався у попередньому пункті. Розглянемо докладніше випадок k = 2, тобто біграмний лінійний шифр. В якості ключа вибирається матриця

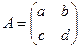
з коефіцієнтами a,ь,c,d Є Zn. Матриця А повинна бути оборотною. За твердженням Б.5 це рівнозначно умові НСД (w, n) = 1 для w = ad — ьс — визначника матриці. За цієї умови з допомогою розширеного алгоритму Евкліда ми можемо знайти в Zn обернений елемент w-1 і за формулою оберненої матриці обчислити дешифруючий ключ
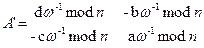
Наприклад, для 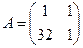 над Z33 маємо w = 2. За розширеним алгоритмом Евкліда знаходимо w-1 = 17 (див. приклад 2.9) і
над Z33 маємо w = 2. За розширеним алгоритмом Евкліда знаходимо w-1 = 17 (див. приклад 2.9) і 
Нехай потрібно зашифрувати повідомлення завтра. Першій біграмі за відповідає вектор 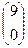 . Множення на матрицю А дає
. Множення на матрицю А дає  . Таким же чином знаходимо образи біграми вт та ра.
. Таким же чином знаходимо образи біграми вт та ра.
Насамкінець перетворюємо стовпчики отриманої матриці у біграми і отримуємо криптотекст зффррй.
Дешифрування відбувається так само, лише із використанням оберненої матриці. Наприклад, якщо ми маємо криптотекст рьгк, то розбиваємо його на біграми 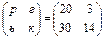 і виконуємо множення на матрицю А':
і виконуємо множення на матрицю А':
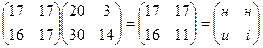
В результаті дістаємо повідомлення нині.
Повернемось до загального аналізу лінійного шифру. Співвідношення D(E(X)) = X для будь-якого X 
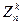 випливає з рівностей А' (АХ) = (А'А)Х = IkX = X , де Ік — одинична матриця порядку k. Дешифруючий ключ А' для вибраної оборотною матриці А обчислюється ефективно за формулою для оберненої матриці (див. пункт Б. 6). Потрібне для цього значення (detA)-1 mod n знаходиться за допомогою розширеного алгоритму Евкліда (приклад 2.9). На довершення доведемо, що необоротні матриці А непридатні для використання в якості ключа.
випливає з рівностей А' (АХ) = (А'А)Х = IkX = X , де Ік — одинична матриця порядку k. Дешифруючий ключ А' для вибраної оборотною матриці А обчислюється ефективно за формулою для оберненої матриці (див. пункт Б. 6). Потрібне для цього значення (detA)-1 mod n знаходиться за допомогою розширеного алгоритму Евкліда (приклад 2.9). На довершення доведемо, що необоротні матриці А непридатні для використання в якості ключа.
Твердження 3.5. Відображення Е : 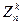

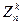 , задане формулою Е(Х) = АХ, має обернене тоді і тільки тоді, коли А
, задане формулою Е(Х) = АХ, має обернене тоді і тільки тоді, коли А GLk(Zn).
GLk(Zn).
Доведення. При А GLk(Zn) існування відображення, оберненого до Е, було встановлене вище. Навпаки, припустимо, що Е має обернене відображення D. Позначимо через Хі,
GLk(Zn) існування відображення, оберненого до Е, було встановлене вище. Навпаки, припустимо, що Е має обернене відображення D. Позначимо через Хі,
1  і
і  k, вектор з і-тою компонентою 1 і з рештою компонент, що дорівнюють 0. Розглянемо матрицю U із стовпчиками D(X1), . . . , D(Xk). Зауважимо, що AU = Ik, тобто матриця U є правою оберненою до А. Отже, матриця А оборотна (див. твердження Б. 5).
k, вектор з і-тою компонентою 1 і з рештою компонент, що дорівнюють 0. Розглянемо матрицю U із стовпчиками D(X1), . . . , D(Xk). Зауважимо, що AU = Ik, тобто матриця U є правою оберненою до А. Отже, матриця А оборотна (див. твердження Б. 5).
Тепер на черзі
Читайте також:
| <== попередня сторінка | | | наступна сторінка ==> |
| Доведення. | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |