• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Доведення.

Випадок 1: п = р — просте.

Для ф_к(р), кількості оборотних матриць порядку k над Z_p, нам належить показати, що

ф_k(p) = 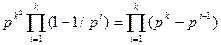(1)

Будемо опиратись на той факт, що Z_p є полем, а відтак оборотність матриці А із M_к(Z_p) рівносильна її невиродженості. Через Х₁, Х₂, • • •, X_k позначимо стовпчики матриці А. Питання, скількома способами можна вибрати матрицю в M_к(Z_p)*, еквівалентне такому - скількома

способами можна вибрати послідовність k лінійно незалежних векторів
Х₁,Х₂,... X_k в

Вектор Х₁ можна вибрати довільним за винятком нульового, тобто p_k - 1 способом. Далі, для 1 < і < k лінійна оболонка векторів Х₁,Х₂,... X_i-1 є (і-1) -вимірним векторним підпростором простору , і Х_і може бути довільним вектором поза цим підпростором. (і — 1)-вимірний підпростір містить p^і-1 елементів, тому для вибору X_і є p^k — р^і-1 можливість. Звідси випливає (1).

Випадок 2: п = 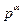, де р просте.

Ми доведемо рівність

ф_k(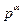) = 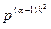ф_k(p) (2)

Легко зауважити, що з врахуванням (1) з неї випливатиме те, що потрібно.

Для А Є M_к(Z_p) позначимо через 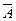Є M_к(Z_p) матрицю, коефіці;нти якої є лишками за модулем р відповідних коефіцієнтів матриці А. Матриця А оборотна тоді і лише тоді, коли такою є матриця .

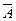Це випливає з тверджень Б.5 і 2.8. Справді, det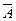= detAmodp, звідки
НСД (det A, 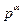) = НСД (det 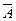,р). Кількість матриць 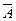в M_к(Z_p)* Дорівнює ф_k(p).Кожна така матриця має 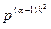прообразів А в

M_к(Z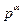), які отримуються додаванням будь-якого із 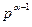чисел pj, 0 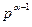-1 до кожного із k² коефіцієнтів матриці 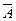. Звідси маємо рівність (2).

Випадок 3: п = ...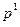

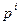
Цей, загальний, випадок зводиться до випадку 2 за мультиплікатністю функції ф_k(n) (наслідок 2.18). Дійсно,

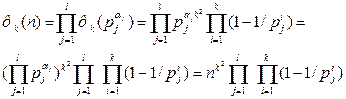
що й слід було довести...

ВПРАВИ

2.1. Обчислити а) 1212121 mod 9; b) (-1212121) mod 9.

2.2. Обчислити НСД (959, 791).

2.3. Послідовність Фібоначчі задається рекурентним співвідношен f₁= f₂=1, f_n= f_n-1+ f_n-2

a) Довести, що алгоритм Евкліда при обчисленні НСД(f_n, f_n-1) робить п — 2 кроки.

b)Довести, що при обчисленні НСД (а, b), де а b, алгоритм Евклідa робить не більше кроків, ніж при обчисленні НСД (f_n, f_n-1), де п таке, що f_n ь<f_n-1.

c) Довести, що при обчисленні НСД(а,b), де а b, алгоритм Евкліда робить не більше, ніж log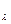b + 1 крок, де 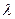= (1 +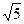)/2. Показати, що ця оцінка оптимальна з точністю до адитивної константи.

2.4.Довести, що НСД є асоціативною бінарною операцією на множині натуральних чисел.

2.5.Найменше натуральне число, яке ділиться на кожне із невід'ємниx цілих чисел
а₁,…a_m називається їхнім найменшим спільним кратним (НСК) і позначається НСК (а₁,…a_m). Довести, що

а)НСД (а, b) • НСК (а,b) = ab для натуральних а і b;

b)НСК (а, b) = аb для взаємно простих а і b.

2.6. Знайти цілі u і v такі, що 137 u + 113 v = 1.

2.7. Довести, що НСД (a, b) дорівнює найменшому додатному числу вида ua + vb, де u і v цілі.

2.8. Довести твердження 2.5 та 2.6.

2.9. За допомогою конгруенцій довести відомий критерій: число ділиться на 9 тоді і тільки тоді, коли на 9 ділиться сума цифр його десяткового зпису

2.10. Знайти канонічний розклад числа 1934064 на прості співмножники

2.11. Знайти 8^-1mod 35.

2 12. Знайти число, яке при діленні на 137 і 113 дає остачі 40 і 50 відповідно.

2 13. Обчислити значення ф(п) для всіх п < 20.

2.14.Для яких п значення ф(п) непарне

2.15. Знайти всі п, для яких ф(п) < 5.

ЛІТЕРАТУРА

Теоретико-числовий матеріал цього параграфу покривається підручниками [13, 30]. Оцінка m < 21og2ь + 1 на кількість кроків алгоритму Евкліда зауважена в [1]. Асимптотичне кращу оцінку m < 51og10ь довів у 1844 році Ламе (див. [32, розділ 4.5.3] або [3, розділ 2.2.2], а також вправу 2.3). Низка вдосконалених варіантів алгоритму Евкліда викладена в [62, 3] та [32, розділ 4.5.2].

Чимало фактів, доведених нами для цілих чисел, поширюються на інші кільця. Найбільший спільний дільник мають будь-які два ненульові елемен­и в довільному кільці головних ідеалів. Якщо таке кільце евклідове, то найбільший спільний дільник знаходиться ефективно за допомогою аналогу алгоритму Евкліда. Прикладом може служити кільце многочленів від одної змінної над полем (див. пункт Б.8). Для кожного кільця головних ідеалів справедливий аналог теореми про однозначний розклад на прості множники [11, 37, ЗО].

У нашому викладі теорема Ойлера була виведена із теореми Лагранжа.Коротке пряме доведення наведене в [13]. Узагальнення Китайської теореми про остачі для довільних комутативних кілець з одиницею можна знайти в [37, § ІІ.2] або [2, Тв. 12.3.1].

ЛЕКЦІЯ 7

Читайте також:

1. Доведення.
2. Доведення.
3. Доведення.
4. Доведення.
5. Доведення.
6. Доведення.
7. Доведення.
8. Доведення.
9. Доведення.
10. Доведення.
11. Доведення.

Переглядів: 1113