Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Арифметика

2.1 Алгоритм Евкліда. Для будь-якого цілого а і натурального b однозначно визначені цілі числа g і г такі, що а = bq+r i 0 < г < b. Число q називається часткою, а r — остачею вiд ділення а на b. Наприклад, рівність -20 = (-1) • 67 + 47 означає, що -20 при діленні на 67 дає частку -1 і остачу 47. Для остачі будемо вживати таке позначення: r = a mod b. Число r будемо також називати (зведеним) лишком числа a за модулем b. Якщо г = 0, то кажуть, що а ділиться на b (націло або без остачі) і пишуть b | а. Кажуть також, що b ділить а, і називають b дільником числа а, а а — кратним числа b. Запис b|-а означатиме, що а не ділиться на b. Для цілих а і b через НСД (а, b) позначається їх найбільший спільний дільник (НСД) — найбільше з-поміж таких c що одночасно с |а і с | b (хоча б одне із а і b вважається відмінним від нуля). Числа а і b називаються взаємно простими, якщо НСД (а, b) = l

Aлгоритм Евкліда (3 ст. до н.е.) для знаходження НСД двох натуральних чисел a і b грунтується на співвідношеннях:

1) НСД(а,b) = НСД(b,а mod b) для ab

2) НСД(а, 0) = а

Спершу продемонструємо ідею цього алгоритму на прикладі.

Приклад 2.1. Щоб знайти НСД (211,79), застосовуємо послідовно (1) аж доки не опинимось у ситуації, коли можна використати (2). Таким чином робота алгоритму зводиться до кількаразового ділення з остачею.

211 = 792 + 53

79 = 531 + 26

53 = 262 + 1

26 = 126 + 0

Маємо НСД (211,79) = НСД (79,53) = НСД (53, 26) = НСД (26,1) = НСД (1,0) = 1.

Опишемо тепер, що відбувається в загальному випадку.

Алгоритм Eвкліда обчислення НСД (а, b), аb.

· Покласти г₀ = а, г₁ = b, і = 1.

· Виконати i-ий крок, що полягає у діленні з остачею:

r_і-1 = r_іq_i + r_і₊₁. (З)

· Якщо r_і₊₁ > 0, то збільшити і на 1 і перейти до виконання наступнoго кроку згідно з попереднім пунктом. Якщо r_і₊₁ = 0, то завершити роботу із результатом НСД (а, b) = г_i.

Коректність. Алгоритм завершує роботу як тільки r_і₊₁ = 0. Рано и пізно це трапиться, оскільки 0 < r_і₊₁< г_i, для кожного і. Припустимо так сталося на m-ому кроці, тобто r_m₊₁ = 0. Результатом роботи алгоритму є значення r_m. Рівність r_m = НСД (а, b) випливає з таких міркувань. Співвідношення НСД (а, b) = НСД (r_і-1, r_і) для 1 і m+1 доводиться індукцією з використанням (1). При і = m + 1 із врахуваням (2) отримуємо НСД (а, b) = НСД (r_m, 0) = r_m.

Ефективність. Під ефективністю алгоритму Евкліда розуміємо те що кількість кроків m, які виконуються на вході а, b, не є надто великою. Із співвідношення 0 < r_і+1< г_i,- випливає, що mb. Однак ця оцінка є незадовільною. Скажімо, для чисел а і b з якоюсь сототнею цифр у десятковому записі кожного, нам гарантовано лише, що на знаходження їх НСД буде витрачено не більше 10100 кроків. Але найбільш швикодіючій ЕОМ для виконання такої кількості кроків потрібен фантастично великий обсяг часу.

На щастя, оцінку на m можна суттєво поліпшити. Покажемо, що m2logь+1. Для цього використаємо нерівність r_і+1< r_і-1/2. Вона доводиться розглядом двох випадків: якщо r_і< r_і-1/2, то використовуємо нерівність r_і+1< r_і; якщо ж r_і< r_і-1/2, то використовуємо рівність r_і+1 = r_і-1 mod r_і. Таким чином, кожні два кроки зменшують r_і+1 принаймні вдвічі, і не пізніше, ніж за 21og₂ь+1 кроків ми прийдемо до r_і+1 = 0.

Алгоритм Евкліда дає такий наслідок.

Твердження 2.2. Для кожної пари взаємно простих чисел а і ь можна знайти такі цілі u і v, що иа + vь = 1.

Доведення. За умовою НСД (а, b) = 1. Тому на передостанньому кроці алгоритму Евкліда матимемо r_m_-2 = r_m_-1 q_m_-1+1. Звідси 1 = 1r_m_-2+(- q_m_-1) r_m_-1 Використавши це як базу для зворотньої

індукції за і від m-1 до 1, доведемо, що 1 = и_i₊₁r_i+v_ir_i, для деяких цілих и_i та v_i,. Справді, якщо 1 = и_i₊₁r_i+v_i₊₁r_i₊₁, то після підстановки замість r_i₊₁ його значення, визначеного з (3), маємо
1 = v_i₊₁r_i_-1+(u_i₊1-q_iv_i₊₁)r_i.

При і = 1 отримуємо потрібне твердження.

Зазначимо, що алгоритм Евкліда дає ефективний спосіб знаходження коефіцієнтів u і v; для заданої пари а, b.

Приклад 2.3. Нехай а = 211, b = 79. Протокол роботи алгоритму Евкліда виписаний у прикладі 2.1. Рухаючись знизу вверх, отримуємомо

1 = 153 + (-2) 26 = 153 + (-2) (79 - 153) = (-2) 79 +353 = (-2) 79 + 3(211 - 279) = 3211 + (-8) 79.

Отже, u = 3 і v = - 8. Продемонстрований спосіб визначення коефіцієнтів u і v є наочним, але не оптимальним, бо вимагає збереження в пам'яті проміжних обчислень алгоритму Евкліда. Кращий спосіб, так званий розширений алгоритм Евкліда, пропонується у вправі 2.7.

2.2. Розклад на прості співмножники.Очевидно, що кожне натуральне число а має принаймні два дільники, а саме 1 і а. Ці дільники називаються тривіальними. Якщо число а не має ніяких інших дільників, то воно називається простим, в іншому ж разі — складеним.

Твердження 2.4. Якщо просте число р ділить добуток ab двох натуральних чисел, то воно мусить ділити хоча б одне із чисел а і b.

Доведення. Якщо а не ділиться на р, то а і р взаємно прості. Тоді за твердженням 2.2 для деяких цілих чисел u і v виконується рівністі иа + vp = 1. Домноживши її на b, отримаємо
uab + vbp =b. Оскільки р | аb, то ліва частина ділиться на р, а відтак р | b.

Зрозуміло, що кожне складене число можна записати як добуток простих. Такий добуток називається розкладом числа на прості співмножники. Вважаємо, що розклад простого числа складається з єдиного елемента — самого числа. Має місце

Теорема про однозначність розкладу на прості співмножники! Кожне більше від 1 ціле число однозначно розкладається на прості співмножники (якщо не враховувати їхнього порядку).

Доведення. Припустимо, що 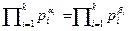— Два різні розклади одного й того ж числа на прості співмножники. Тоді мусить бути для деякого j. Якщо , то маємо p_j | 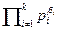, що суперечить твердженню 2.4. Випадок 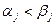розглядається симетрично.

Розклад, в якому прості співмножники йдуть у неспадному порядку, називається канонічним.

ЛЕКЦІЯ 6

2.3. Конгруенції. В пункті 2.1 ми домовились позначати остачу від и ділення цілого а на натуральне b через a mod b. Позначення mod ми будемо вживати і в іншому значенні. А саме, ми будемо писати х = у (mod п), якщо цілі х і у при діленні на натуральне п, дають однакову остачу. Такі х і у називатимемо конгруентними або рівними за модулем п. Відношення між х і у називається конгруенцією або порівнянням.

Твердження 2.5. Наступні три умови еквівалентні.

1. х = у (mod п).

2. х = у + kn для деякого цілого k.

3. п|(х-у).

Твердження 2.6. Конгруенції мають такі властивості.

1) Це відношення еквівалентності:

1. х = х (mod п) (рефлексивність);

2. якщо х = у (mod п), то у = х (mod n) (симетричність);

3. якщо х = у (modn) і у = z(modn), то х = z(modn) (транзитивність).

2) Конгруенції можна почленно додавати: якщо х₁ = y₁ (modn) i х₂ = y₂(modn), то
х₁+х₂=y₁+y₂(modn). Зокрема, до обох ,.частин конгруенції можна додавати одне й те ж число.

3) Конгруенції можна почленно перемножувати: якщо х₁ = y₁ (modn) і х₂ = y₂(modn),, то х₁х₂=y₁y₂(modn). Зокрема, обидві частини конгруенції можна домножувати на одне й те ж число.

4) Обидві частини конгруенції можна скорочувати на їхній спільний дільник, якщо він взаємно простий з модулем: якщо d |x, d| у і НСД (d, п) = 1, то з х = у (mod n) випливає x/d = y/d(modm).

5) Обидві частини конгруенції і модуль можна скорочувати на їхній спільний дільник: якщо d | х, d | у i d | п, то з х = у (modn) випливає x/d = y/d (mod n/d).

6) Якщо m | n, то з х = у (mod n) випливав х = у (mod m).

7) Для р і q простих, х = у (mod pq) тоді і лише тоді, коли одночасно x = y(modp) i x=y(modq).

Приклад 2.7.Уникаючи обчислювальної роботи, покажемо, що 73524 ділиться на 11. Очевидно, 10 = -1 (mod 11). Множачи цю конгруенцію саму на себе, отримаємо: 100 = 1 (mod 11), 1000 = - 1 (mod 11), 10000 = 1 (mod 11). Після домноження на числа 2, 5, 3, 7 відповідно, матимемо: 20 = -2 (mod 11), 500 = 5 (mod 11), 3000 = -3 (mod 11), 70000 = 7 (mod 11). Почленне сумування дасть 73520 =.7 (mod 11). Додавши до обох частин 4, отримаємо 73524 =11 = 0 (mod 11).

2.4. Кільце лишків. Для натурального п через Z_n позначаємо множину {0,1,..., п - 1}, наділену операціями додавання та множення за модулем п. Сумою х і у із Z_n(х+у) mod п, а їх добутком є (ху) mod n. Відносно цих операцій Z_n є комутативним кільцем з одиницею, яке називається кільцем зведених лишків за модулем п. Через Z* позначаємо мультиплікативну групу елементів, для яких в Z_n є обернені відносно множення.

Твердження 2.8. Z* складається з елементів х, взаємно простих з n, і лише з них.

Доведення. Якщо НСД(x, n) = 1, то за твердженням 2.2 маємо ux+ vn = 1 для деяких цілих u і v. Звідси ux = 1 (mod n) і х' = u mod n в оберненим за множенням до х в Z_n.

Навпаки, якщо хх' = 1 в Z_n, то добуток х та х' як цілих чисел дає , 1 при діленні на п:
хх' = qn + 1. Отже, кожен спільний дільник ж та п ділить також 1, звідки НСД (х, п) = 1

З доведення твердження бачимо, що розширений алгоритм Евкліда дає ефективний спосіб знаходження оберненого елемента для будь якого заданого х Z_n*

Елемент, обернений до хZ_n* відносно множення, будемо позначати через
х^-1modn бо просто х^-1 Ділення на х в Z_n означатиме множення на х^-1 . Елемент, обернений до
х Z_n* відносно додавання будемо позначати через -х. Зокрема, - 1 = п - 1 в Z_n. Як звичайно ,в Zn можна ввести операцію віднімання: х — у = х + (— у).

Приклад 2. 9. Нехай ми хочемо знайти елемент, обернений до 79 в Z*₂₁₁. У прикладі 2.3 була отримана рівність 1 = 3211 + (—8) 79. з неї негайно випливає (-8) 79 1(mod211). Отже, 79^-1 mod 211 = (-8) mod 211 = 203.

Наслідок. 2.10. Для простого модуля р, кільце Z_p є полем.

Через ф(п) позначаємо порядок групи Z_n*. Іншими словами, значення ф(п) дорівнює кількості натуральних чисел, що не перевищують п взаємно прості з п. ф називається функцією Ойлера.

Теорема Ойлера (1763). Для взаємно простих цілого х і натурального п справедлива конгруенція х^ф(ⁿ⁾ = 1 (modn).

Доведення.Припустимо 1 < х < п і розглянемо х як елементи мультиплікативної групи Z_n*. За теоремою Лагранжа порядок елемента х є дільником порядку групи, ф(п) в нашому випадку. Тому х^ф(ⁿ⁾ = 11 в Z_n*, звідси й випливає теорема.

Випадок довільного х зводимо до попереднього, використавши конгруенцію Z_n* = (х mod п)^ф(ⁿ⁾ (mod n).

Як легко бачити, ф(р) = р — 1 для простого р. Звідси отримуємся такий наслідок теореми Ойлера.

Мала теорема Ферма(1640). Якщо ціле х не ділиться на прості р, то х^р-1 = 1 (modp)

Китайська теорема про остачі (І ст. до н.е.). Для будь-якої пари взаємно простих натуральних чисел п₁ і п₂ та для будь-якої пари цілих чисел х₁ і х₂, можна знайти таке ціле х, де х = х₁ (modn₁) і х = х₂ (mod п₂).

Доведення. За твердженням 2.2 для деяких цілих u₁ і и₂ маємо рівність u₁n₁+u₂n₂ = 1, з якої випливають співвідношення u₁n₁= 1 (modn₂) і u₂n₂ = l(modn₁). Використовуючи останні, легко пересвідчитись, що х = х₂ u₁n₁ + х₁ u₂n₂ задовільняє потрібні умови.

Як видно з доведення, х для заданих n₁, n₂, х₁ і х₂ знаходиться ефективно за допомогою розширеного алгоритму Евкліда.

Приклад 2.11. Нехай ми хочемо знайти ціле х, яке при діленні на 211 давало б остачу 100, а при діленні на 79 остачу 10. У прикладі 2.3 була отримана рівність
1 = 3211 + (—8)79. Отже, в якості х можна взяти 103211 +100(—8) 79 = —56870. Зрозуміло, що це число можна замінити його остачею від ділення на 21179 = 16669. В результаті отримуємо 9806.

Твердження 2.12. Нехай п = n₁n₂, де n₁, n₂ взаємно прості. Тоді відображення
f : Z_n Z_n₁Z_n₂, задане співвідношенням

f(x) = (х mod n₁,x mod n₂), (1)

є Ізоморфізмом кілець.

Доведення. Перевірка того, що f є гомоморфізмом, зводиться до перевірки того, що відображення f_і(x) = (х mod n), є гомоморфізмом із Z_n в Z_n_і для і = 1,2. Останнє справді має місце, оскільки п_і, ділить п.

Сюр'єктивність є безпосереднім наслідком Китайської теореми остачі.

Ін'єктивність випливає із тривіальності ядра — найменшим натуральним числом, яке ділиться націло на кожне із взаємно простих чисел n₁, n₂є добутком n₁n₂=n

Слід зауважити, що як f, так і обернене відображення f^-1 обчислюються ефективним чином (див. приклад 2.11).

Попереднє твердження разом із твердженням Б.2 дає

Наслідок 2.13. Нехай п = n₁n₂, де n₁ і n₂ взаємно прості. Тоді звуження відображення (1) на Z_n* є ізоморфізмом із цієї групи на прямий добуток груп Z_n₁*Z_n₂*

Наслідок 2.14. (мультиплікативність функції Ойлера) Для попарно взаємно простих
n₁, n₂,..., n_l справедлива рівність ф(n₁, n₂ ... n_l) = ф(n₁) ф(n₂) ... ф(n_l).

Доведення. Випадок l = 2 безпосередньо випливає з наслідку 2.13. загальне твердження доводиться індукцією за l.

Формула для функції Ойлера. Нехай п =...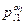— розклад натурального числа п на прості співмножники. .Тоді ф(п) = п(1 —1/p₁)x….x(1-p/p_l)

Доведення. Спочатку розглянемо випадок l = 1, тобто п = 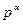для деякого Простого р. Числами, які не перевищують число 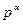і п взаємно прості з ним, є р, 2р, Зр,..., 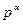= 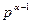р всього 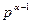штук. Звідси ф(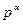) = 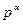-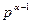Для l>1 формула випливає з мультиплікативності функції Ойлера.

Твердження 2.15. ф(п) > n(61nlnn) для п > 4. ; доведення, проведене в [135]. Див. також [13, вправа II.9(g)].

2.5. Кільце Матриць,. Через M_к(Z_n) позначаємо множину матриць розміру k х k з коефіцієнтами з Z_n. З операціями додавання і множення матриць M_к(Z_n) утворює кільце.
M_к(Z_n) * = GL_k(Z_n) служить позначенням для мультиплікативної групи оборотних матриць Порядок цієї групи позначимо через ф_к(п). Зрозуміло, що ф₁(п) є нічим іншим як функцією Ойлера. у цьому пункті ми виведемо формулу для ф_к(п) де k довільне натуральне число. Будемо діяти за тим же планом що був реалізований Для функції Ойлера.

Твердження 2.16. Нехай п = n₁n₂, де n₁ і n₂ взаємно прості Тоді відображення f_k : M_к(Z_n)M_к(Z_n1)M_к(Z_n2) , яке співставтляє матриці А пару матриць А1 та А2, коефіцієнти яких є лишками відповідних коефіцієнтів матриці А за модулями n₁ і n₂, є ізоморфізмом кілець.

Доведення. Очевидно, що f_k переводить одиницю кільця M_к(Z_n) в одиницю кільця M_к(Z_n1)M_к(Z_n2). Нескладно перевірити також що f_k зберігає Операції додавання та множення; ключовим фактом при цьому є те, що п ділиться на n₁ і n₂. Отже, f_k є гомоморфізмом

Щоб встановити сюр'єктивність, зауважимо, що f_k діє покомпонентно і на кожній із k² компонент це відображення є сюр'єктивним за Китайською теоремою про остачі.

Ін'єктивність випливає із тривіальності ядра.

За твердженням Б.2 отримуємо

Наслідок 2.17. Звуження відображення f_k на M_к(Z_n)* є ізоморфізмом Із цієї групи на прямий добуток груп M_к(Z_n1)* х M_к(Z_n2)*

Наслідок 2.18. Функція f_k мультиплікативна: для попарно взаємно простих n₁ n₂,..., n_l, справедлива рівність ф(n₁, n₂ ... n_l) = ф(n₁) ф(n₂) ... ф(n_l).

Доведення.Випадок l = 2 безпосередньо випливає з наслідку 2.17 Загальне твердження доводиться індукцією за l.

Теорема 2.19. Нехай п =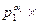...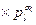— розклад натурального п на прості співмножники. Тоді ф_k(n) =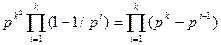

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Формалізм	\|	Доведення.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.009 сек.