• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Формалізм

Елементарна криптографія : математичний підхід

Розділ II.

Звід математичних понять та теорем, що зустрічаються в цьому розділі, міститься в додатку Б.

1.1. Абетка II. Алфавітом називаємо довільну скінченну множину. Типовими прикладами, які зустрічаються у нашому курсі, є

{а, б, в, г,..., ь, ю, я} - український алфавіт,

{_, а, б, г,..., ь, ю, я} - він же з пропуском між словами,

{_,.,!,?, а, б, г,..., ь, ю, я} - він же з розділовими знаками,

{0, 1}⁶ - всі 0-1 – послідовності довжини 6,

Z₃₃ = {0,1,2,..., 32} - кільце лишків за модулем 33.

Алфавіти позначатимемо рукописними літерами A, В і т.д. Елементи алфавіту називатимемо символами або буквами, навіть якщо це буде розходитись із звичним вживанням останнього терміну. Наприклад, цифра 1, і число 10 є буквами алфавіту Z₃₃. Слово в алфавіті A — це скінченна послідовність букв цього алфавіту. A* служитиме позначеням для множини всіх слів у алфавіті A. Довжина слова — це кількісі букв у ньому. Зрозуміло, що множина слів у алфавіті A довжини l є нічим іншим як декартовим степенем A^l. Довжину слова w позначатимемо як |w|. Для слів v і u через vu позначатимемо результат їх злиття в одне слово, саме в такому порядку. Слово v називатимемо префіксом слова w. У випадку, коли v = w або w = vu для деякого слова и.

Коли говорять про криптосистему чи шифр, мають на увазі такі об'єкти:

· Алфавіт А, в якому записуються повідомлення (відкриті тексти}. Повідомлення М є словом в алфавіті А (яке може складатися з багатьох слів у звичному лінгвістичному розумінні), тобто М Є А*. Множина А* називається простором повідомлень або відкритих текстів.

· Алфавіт В, в якому записуються криптотексти. Множина В* називається простором криптотекстів. Часто А = В.

· Простір ключів К, який складається із слів у деякому алфавіті, що називаються ключами.

· Шифруюче відображення Е : КА* В*.

· Дешифруюче відображення D : КВ* А*. Відображення Е і D повинні мати таку властивість:

D(K, Е(К, М)) - М для всіх М А* і К К.. (1)

Фіксація ключа К визначає відображення Ek: А* В* за формулою Ек(М) = Е(К,М) для кожного М А*. Подібним чином задається й відображення Dk: В* А*

Властивість (1) по-іншому можна сформулювати так: для будь-якого К дешифруюче відображення. Dk: В* А* є оберненим зліва до шифруючого відображення Ek: А* В*. З теореми про обернене відображення (див. додаток Б) випливає, що Ek мусить бути ін'єкцією. Цілком зрозуміло, що ця умова рівнозначна принциповій можливості дешифрування. Навпаки, на підставі тієї ж теореми будь-яка родина ін’єктивних відображень {Ек : А* В*} _kk може розглядатись як шифруюча в тому плані, що для них існують обернені зліва відображення {Dк : В* А*} _kk, які можуть вважатися дешифруючими.

Дуже часто у конкретних криптоситемах шифруюче відображення Ек крім ін'єктивності володіє також сюр'єктивністю. За теоремою про обернене відображення, дешифруюче відображення Dк є оберненим до Ек не тільки зліва, а й справа — обставина, що має криптографічні застосування. Таким чином, у цьому випадку Ек і Dк є взаємно оберненими:

Dk(Ek(M)) = Ek(Dk(M)) = М.

Криптосистему називаємо ефективною, якщо шифруюче і дешифруюче відображення

реалізуються швидкими алгоритмами. Навряд чи для читача хоча б з невеликим досвідом програмування таке формулювання потребує уточнення. Ті ж читачі, яких турбує дещо неформальний характер поняття ефективності, повинні отримати певне полегшення від ознайомлення з розділом III.

Питання, які криптосистеми слід називати надійними, детально обговорювалось у попередньому розділі і залишатиметься предметом при­скіпливого розгляду й надалі. ,

Шифр називається блоковим з періодом l, якщо шифруюче відображення задається спочатку на словах довжини l, тобто маємо Е : K А^l В*, а після цього поширюється на слова довільної довжини наступним чином. Якщо М = M₁M₂…M_t, де блоки М_і, і t, мають довжину l, то Е(К,М) = E(K,M₁)E(K,M₂)...E(K,M_t). Якщо ж останній блок M_t має меншу від l довжину, то він доповнюється до повного довільним наперед обумовленим чином.

Часто у блоковому шифрі шифруюче відображення зберігає довжину, тобто є вигляду Е : К А^l В^l. Окрім того множини А^l і В^l можуть містити однакову кількість слів, як це буде, скажімо, в поширеному випадку А = В. Якщо ми маємо відображення саме такого виду і розглядаємо питання, чи можна його використовувати як шифруюче, то в пригоді знову стає теорема про обернене відображення. Згідно з нею досить довести якусь одну з чотирьох умов: 1) ін'єктивність, 2) сюр'єктивність, 3) існування оберненого зліва відображення, 4) існування оберненого справа відображення.

1.2. Дешифрування ітераціями. В цьому пункті ми розглядаємо блоковий шифр із шифруючим відображенням виду Е : К А^l A^l (алфавіт криптотекстів збігається з алфавітом повідомлень). Зрозуміло, що для кожного ключа К шифруюче відображення ек є елементом групи Sym A^l, де SymX позначає групу перестановок множини X. Принагіднo означимо формально поняття, введене на стор. 40: шифр Е : К А^l A^l утворює групу, якщо родина {Ек} _kk є в Sym A^l підгрупою.

Шифруюче відображення Еk : А^l A^l можна застосовувати кілька разів. Відображення Е^sk : А^l A^l означимо індуктивнo: Е¹к = Ek, Еⁱк = Eк о Е^i-1к для і > 1. Еⁱк будемо називати і-кратною ітерацією або і-тим степенем відображення Eк.

Методом ітерацій суперник може скористатися у разі, коли він має доступ до шифруючого відображення із фіксованим ключем (хоча не знає, який саме ключ К "зашито" в алгоритм). Підслухавши крипто текст С = Ек(М), суперник може спробувати знайти повідомлення М обчислюючи послідовность Е¹к(С), E²к(C), Е^3к(С),... доти, поки на якумусь m-му кроці не виявиться, що Е^mк(С) = С. Це означає, що повідомлення було отримане на попередньому кроці: М = Е^m-1к(С)

Твердження 1.1. Для шифруючого відображення Е : К А^l A^l метод ітерацій через деяку кількість кроків приводить до успіху. Точніше, якщо алфавіт складається з п букв, то для будь-якого ключа К існує число m < (п^l)! таке, що Е^mк(С) = С для всіх СА^l.

Доведення. В якості m можна взяти порядок відображення Eк як елемента групи SymA^l, який за теоремою Лагранжа не перевищує (п')! порядку цієї групи (див. додаток Б). Тоді для будь-якого СА^l матимемо Е^mк(С) = id_A’(C) = C.

ВПРАВИ

1.1.Дати формальне означення композиції двох шифруючих відображень Е₁ : К₁ А* Ь* і Е₂ : К₂ Ь* С* (повідомлення шифрується спочатку за допомогою Е\, а потім ще раз за допомогою Е₂).

1.2.Дати незалежне від теореми Лагранжа доведення того, що метод ітерацій раніше чи пізніше досягає успіху.

1.3.Довести підсилення твердження 1.1. А саме, для будь-якого ключа метод ітерацій приведе до успіху за не більш як

a)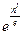кроків, де е = 2, 71828... — основа натуральних логарифмів.

ь) 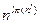кроків, де 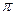(х) — кількість простих чисел, що не перевищують х (див. пункт IV. 1.3).

1.4. Довести, що для розкриття шифру Віженера над n-символьним алфавітом досить п ітерацій.

Переглядів: 831