• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Арифметика II

Складність арифметичних задач

Розділ IV.

У цьому розділі ми вивчаємо складність алгоритмічних задач теорії чисел, на яких грунтується сучасна криптографія.

Насамперед варто зафіксувати певну домовленість стосовно позначень. Коли в теорії чисел йдеться про параметр, що є натуральним числом, його часто позначають через п. Коли в теорії складності йдеться про час роботи алгоритму, п є традиційним позначенням для довжини входу. Обидві традиції не можуть бути дотриманими одночасно, коли йдеться про алгоритм, який отримує на вхід натуральне число. Справді, якщо натуральне число п подається в системі числення за основою k, то його запис має довжину [log_к n] +1. Щоб уникнути двозначності, в цьому розділі ми будемо оцінювати час роботи числового алгоритму як функцію не від довжини, а від величини входу.

Зауважимо, що алгоритм є поліноміальним тоді і тільки тоді, коли час його роботи на вході п (довжини [log_к n] +1!) обмежений функцією c(log_r n)^d для деяких констант с > 0 і d > 1. Алгоритм є експоненцій-ним, якщо на вході п (точніше, на нескінченній послідовності таких входів) час його роботи перевищує cnd для деяких констант с, d > 0.

Перший параграф цього розділу має підготовчий характер. Він містить чергову порцію фактів із теорії чисел, потрібних для побудови та аналізу алгоритмів у наступних параграфах.

1.1. Первісні корені. Нехай р - натуральне число. Ціле число g називається первісним коренем за модулем р, якщо лишок g mod p є твірним елементом групи .

Для простого р група , як мультиплікативна група скінченного поля, є циклічною. Отже, первісні корені існують для всіх простих модулів. Як легко зрозуміти, g є первісним коренем за простим модулем р, якщо послідовність

g⁰ mod р = 1, g¹ mod р, g² mod р, g³ mod р,..., g^p-2mod р (1)

містить всі елементи множини . Остання умова очевидно рівносильна тому, що всі члени послідовності (1) попарно різні.

Приклад 1.1. g = 5 є первісним коренем за модулем р = 23. Послідовність (1) в цьому випадку буде такою: 1, 5, 2, 10, 4, 20, 8, 17, 16, 11, 9, 22, 18, 21, 13, 19, 3, 15, 6, 7, 12, 14. Зауважимо, що черговий член g^k modp не обов'язково обчислювати піднесенням д до k-ro степеня. Простіше домножити вже обчислений попередній член g^k-1mod р на g за модулем р.

Твердження 1.2. Нехай р позначає просте число, і р— 1 = 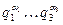— канонічний розклад числа р — 1 на прості співмножники. Тоді

1. в міститься рівно ф(р — 1) первісних коренів за модулем р;

2. щоб число g було первісним коренем за модулем р необхідно і досить, щоб для кожного і s виконувалась умова

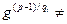l(modp). (2)

Доведення. Пункт 1 випливає безпосередньо із твердження Б.1.

Доведемо пункт 2. Це досить зробити для g . Позначимо через т порядок елемента g в групі . Нагадаємо, що g є первісним коренем за модулем р тоді і тільки тоді, коли т = р — 1.

Якщо умова (2) порушується хоча б для якогось і, то для такого і маємо
т (р — 1)/q_і < р — 1.

Навпаки, припустимо, що умова (2) виконується для всіх і. В цьому випадку повинно бути
т = р — 1. Справді, якби т < р — 1, то за теоремою Лагранжа ми мали б рівність р — 1 = km для деякого k > 1 і як наслідок g^(p-1)/q 1 (modp) для довільного простого дільника q числа k — суперечність з (2).

Приклад 1.3. Для р = 29 маємо 29-1 = 2²7. Оскільки 2¹⁴ 28 ( mod 29) і 2⁴ 16 (mod 29), то g = 2 є первісним коренем за модулем р = 29. На противагу цьому, g = 5 не є первісним коренем за модулем р = 29, бо 5¹⁴ = 1 (mod 29).

1.2. Квадратичні лишки. Нехай п — натуральне число. Ціле х називається квадратичним лишком за модулем п, якщо НСД (х,п) = 1 і х у² ( mod п) для деякого у. В цьому разі у називається квадратним коренем з ж за модулем п. Якщо НСД (х, п) = 1 і х не є квадратичним лишком за модулем п, то х називається квадратичним нелишком за цим модулем. Квадратичні лишки за модулем п, які лежать в межах від 1 до п—1, називаються зведеними. Множину зведених квадратичних лишків будемо позначати через Q_n.

Приклад 1.4. Число 8 є квадратичним лишком за модулем 17. Квадратними коренями з 8 за цим модулем серед натуральних чисел, що не перевищують 17, є 5 і 12. Число 12 є квадратичним нелишком за модулем 17 — воно не має жодного квадратного кореня за цим модулем.

Лема 1.5. Нехай р — непарне просте число. Тоді наступні умови еквівалентні.

1. х є квадратичним лишком за модулем р.

2. x^(Р-1)/2 l(modp).

3. Якщо g . — первісний корінь за модулем р, то для деякого

парного k в виконується рівність х = g^k .

Доведення. 1) 2) Використовуємо те, що х = у²(modn) для деякого у. Тоді рівність 2 справедлива за малою теоремою Ферма.

2) 3) З умови 2 випливає, що х не ділиться на р. Оскільки g — первісний корінь за модулем р, то х = g^k для деякого k. Щоб показати, що k парне, припустимо супротивне. Нехай
х = g^2j+1 Для деякого j. Використовуючи малу теорему Ферма, отримуємо

x^(Р-1)/2 = g^(p-1)j g^(p-1)/2 = g^(p-1)/2

За умовою 2 звідси випливає, що g^(p-1)/2 = 1, а це суперечить тому, що g — первісний корінь.

3) 1) Якщо х = g^2j(modp), то g^j є квадратним коренем з x за модулем р.

Для цілого х і непарного простого р символ Лежандра означується як

Критерій Ойлера. Нехай х — ціле число, а р - непарне просте Тоді

Доведення. У випадку р | х використовуємо еквівалентність умов 1 і 2 з леми 1.5. Залишається показати, що x^(Р-1)/2 = ±1 (modp). Останнє випливає з того, що x^(Р-1)/2 є коренем многочлена X² — 1 в полі , який не може мати більше, ніж два корені 1 і — 1.

Твердження 1. 6. Нехай р — непарне просте, а х₁ і х₂ — цілі числа. Символ Лежандра має такі властивості.

1) Якщо х₁ х₂ (modp), то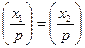

2) Мильтипмкативність: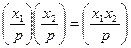

3) Якщо х₂ не ділиться на р, то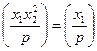

Доведення. Пункт 1 випливає з означення символу Лежандра, а пункт 2 — з критерію Ойлера. Пункт 3 є наслідком пункту 2, оскільки 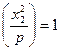— адже очевидно, що , є квадратичним лишком за модулем р.

Нехай п 3 - непарне число з розкладом на прості множники п = 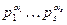. Нехай х — довільне ціле. Тоді символ Якобі 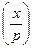, що є узагальненням символу Лежандра, означується як

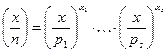
де множники в правій частині є символами Лежандра.

Твердження 1.7. Нехай х,x₁,х₂ — цілі числа, а п,п₁,п₂ – непарні не менші від 3 числа. Символ Якобі має такі властивості.

1) Якщо x₁ х₂ (mod п), то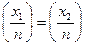

2)

3) Якщо х₂ і п взаємно прості, то

4)

5) Якщо х квадратичний лишок за модулем п, то .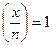

Доведення. Властивості 1 і 2 успадковуються від відповідних властивостей символу Лежандра із твердження 1.6. Пункт 4 справедливий за означенням символу Якобі. Пункт 5 випливає з означень символів Якобі та Лежандра і спостереження, що якщо х є квадратичним лишком за модулем п, то ж є квадратичним лишком також за модулем р для будь-якого р, що ділить п. Пункт 3 є простим наслідком пунктів 2 і 5.

Слід застерегти, що на відміну від символу Лежандра, для символу Якобі обернене до пункту 5 твердження не має місця. Рівність 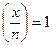можлива навіть тоді, коли х є квадратичним нелишком за модулем п, наприклад, число 2 не є квадратичним лишком за жодним із модулів 3, 5, і 15, але (2/15) = (2/3)(2/5)= (-1)(-1) = 1.

Наступна теорема є одним із центральних результатів теорії чисел.

ЛЕКЦІЯ11

Квадратичний закон взаємності Гауса (1796). Нехай т, п > 2 взаємно прості непарні натуральні числа. Тоді

1. (m/n)(n/m) = (-1)^(m-1)(n-1)/4

2. (2/n) =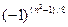

Квадратичний закон взаємності вказує шлях швидкого обчислення 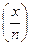для заданих х і п.

Алгоритм обчислення символу Якобі. Можна вважати, що 0 х п, оскільки
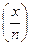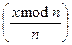= на підставі пункту 1 твердження 1.7. Кожен наступний крок алгоритму зводить обчислення 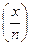до обчислення , де х' < х і п' < п.

· Якщо х = 2^2jy, то за пунктом 3 твердження 1.7 маємо = .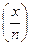

· Якщо х = 2^2j+1y, то за пунктами 3 і 2 твердження 1.7 маємо = =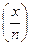

· На підставі пункту 2 квадратичного закону взаємності отримуємо

· Якщо х непарне, то за пунктом 1 квадратичного закону взаємності маємо
=

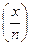Виконання описаних кроків неминуче зведе обчислення 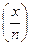до обчислення символу Якобі вигляду (1/n’), який за пунктом 5 твердження 1.7 Дорівнює 1 для довільного непарного п' .

ВПРАВИ

1.15. Нехай

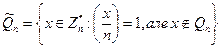
Це так звана множина псевдоквадратів за модулем п. Припустимо, що п = pq є добутком двох різних непарних простих. Довести, що

a) Qn і 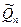мають однакову кількість елементів;

ь) для кожного z Q_n відображення f_z(x) = zx mod п є бієкцією із Qn на .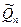

1.16.Нехай р непарне просте. Довести, що

a) (-1/p)=(-1)^(p-1)/2

ь) конгруенція х² — l(modp) має розв'язок для модулів вигляду р = 4k + 1 і лише для них.

c) Довести рівність із пункту а для довільного непарного р.

1.17. Позначимо n-не просте число через р(п): р(1) = 2, р(2) = 3, р(3) = 5 і т.д. З нерівностей пункту 1.3 вивести оцінки

n|nn-O(1)<p(n)<n(ln n + lnln n + +O(1))

1.18.([75]) Використовуючи оцінки попередньої задачі, довести, що задачі обчислення функцій р(п) і 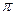(n) поліноміально еквівалентні.

ЛІТЕРАТУРА

Доведення квадратичного закону взаємності Гауса можна знайти в будь-якому із джерел [13, 2, 6]. Доведення оцінок Чебишова для функції 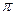(n) міститься у [15].

Читайте також:

1. Арифметика
2. Модулярна арифметика

Переглядів: 1169