
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Рандомізація
3.1. Ймовірнісні алгоритми. Алгоритми, що розглядались досі, називають детермінованими. Більші обчислювальні можливості мають ймовірнісні алгоритми. Окрім входу w, ймовірнісний алгоритм отримує випадкову двійкову послідовність r  {0,1}l, далі працює як звичайний детермінований алгоритм і результат роботи u подає на вихід. Довжина випадкової послідовності l залежить від довжини входу.
{0,1}l, далі працює як звичайний детермінований алгоритм і результат роботи u подає на вихід. Довжина випадкової послідовності l залежить від довжини входу.
Слід підкреслити, що вихід u = u(w, r) ймовірнісного алгоритму залежить не лише від входу, а й від випадкової послідовності. Випадкова послідовність вважається рівномірно розподіленою на {0,1}', тобто кожне r вибирається з ймовірністю 2-1. Ймовірнісний алгоритм розв'язує масову задачу з ймовірністю помилки є, якщо отримавши на вхід індивідуальну задачу w, він подає на вихід її правильний розв'язок з імовірністю не менш ніж 1-е. Іншими словами, вихід алгоритму u = u(w, r) є розв'язком індивідуальної задачі w для всіх, окрім щонайбільше еt випадкових послідовностей г.
Ймовірнісні алгоритми ще називають алгоритмами Монте Карло. Лас Вєгас алгоритми є підкласом алгоритмів Монте Карло. Лас Вегас алгоритм розв'язує задачу з ймовірністю невдачі
е  (0,1), якщо на кожному вході він видає або правильний розв'язок індивідуальної задачі, або повідомлення (на зразок спеціального символу #) про неспроможність такий розв'язок знайти, причому друге має місце з ймовірністю щонайбільше e. Можна вважати, що Лас Вегас алгоритм взагалі не помиляється, лише часом утримується від подання на вихід розв'язку.
(0,1), якщо на кожному вході він видає або правильний розв'язок індивідуальної задачі, або повідомлення (на зразок спеціального символу #) про неспроможність такий розв'язок знайти, причому друге має місце з ймовірністю щонайбільше e. Можна вважати, що Лас Вегас алгоритм взагалі не помиляється, лише часом утримується від подання на вихід розв'язку.
Час робти ймовірнісного алгоритму на вході w означується як максимальна по r кількість кроків, які алгоритм робить на цьому вході з використанням випадкової послідовності r Таким чином поняття поліноміального часу, яке було введене для детермінованих алгоритмів, переноситься й на клас ймовірнісних алгоритмів.
Окремо зупинимось на ймовірнісних алгоритмах для задач розпізнавання. Ймовірнісний (Монте Карло) алгоритм А розпізнає мову L з однобічною помилкою е, де 0 < e < 1, якщо дотримані такі дві умови:
1) якщо w  L, то А приймає вхід w з імовірністю 1;
L, то А приймає вхід w з імовірністю 1;
2) якщо w 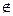 L, то А відхиляє вхід w з імовірністю принаймні 1-е.
L, то А відхиляє вхід w з імовірністю принаймні 1-е.
Нехай ймовірнісний алгоритм А розпізнає мову L з однобічною помилкою е, використовуючи на вході довжини п випадкову послідовність довжини l = l(п). В цьому випадку є ефективний спосіб зменшення помилки. Розглянемо ймовірнісний алгоритм Аt, який на вході w працює наступним чином:
· використовує випадкову послідовність довжини lt, де l = l (|w|), розбивши її на t частин r1,..., rt довжини l кожна;
· моделює роботу алгоритму А на вході w з використанням кожної із випадкових послідовностей r1,..., rt, і отримує t результатів моделювання u1,..., ut, де ui  {0,1};
{0,1};
· подає на вихід 1, якщо всі ui дорівнюють 1, і 0, якщо серед них є хоча б один 0.
Перевіримо, що алгоритм Аt розпізнає ту ж мову L і оцінимо ймовірність помилки. Якщо
w  L, то алгоритм А видає 1 незалежно від вибору випадкової послідовності. Тому ui = 1 для всіх i
L, то алгоритм А видає 1 незалежно від вибору випадкової послідовності. Тому ui = 1 для всіх i  t, і у цьому випадку Аt приймає w з ймовірністю 1. Якщо w
t, і у цьому випадку Аt приймає w з ймовірністю 1. Якщо w 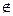 L, то ui = 1 з ймовірністю щонайбільше є, для кожного і. Оскільки r1,..., rt є випадковими і незалежними між собою, то рівність ui = 1 виконується для всіх і
L, то ui = 1 з ймовірністю щонайбільше є, для кожного і. Оскільки r1,..., rt є випадковими і незалежними між собою, то рівність ui = 1 виконується для всіх і  t з ймовірністю не більшою ніж еt. Приходимо до висновку, що А( приймає w не з L із ймовірністю щонайбільше et і, таким чином, розпізнає L з однобічною помилкою еt).
t з ймовірністю не більшою ніж еt. Приходимо до висновку, що А( приймає w не з L із ймовірністю щонайбільше et і, таким чином, розпізнає L з однобічною помилкою еt).
Важливе зауваження полягає в тому, що якщо алгоритм А поліноміальний, то таким є і алгоритм Аt, причому не лише для t константи, а й для будь-якого t(n) — поліному від довжини входу. Поклавши t(n) = cn для відповідної константи с, бачимо, що якщо множина розпізнається поліноміальним ймовірнісним алгоритмом із однобічною помилкою e, для константи е між 0 і 1, то ця ж множина розпізнається деяким поліноміальним алгоритмом із однобічною помилкою 2-n. Ймовірність такого порядку називають експоненцгйно низькою. Таким чином, експоненційне зниження помилки (до еt) досягається ціною всього лише лінійного збільшення часу роботи (у t разів).
3.2. Випадковий вибір. Генерування послідовності випадкових бітів на практиці є не такою простою справою, як може видатись на перший погляд, адже реальна обчислювальна машина не має ніякого механізму для "підкидання монетки". Ми повернемось до цього питання в Розділі VI, а до того моменту будемо вважати, що ймовірнісний алгоритм здатен отримати як завгодно довгу
послідовність випадкових бітів, причому на отримання одного біту йде один крок роботи алгоритму.
У подальшому викладі конкретних ймовірнісних алгоритмів ми вживатимемо приписи на кшталт "вибрати випадковий елемент х із скінченної множини X". Це означає, що елемент х має бути сконструйованим певним чином із випадкової послідовності r, причому кожен з елементів множини X мусить отримуватися з однаковою ймовірністю. Спосіб такого конструювання найчастіше буде доволі очевидним. У цьому пункті ми заздалегідь розберемо кілька простих випадків, які далі зустрічатимуться без детальних пояснень.
Найпростіше влаштувати випадковий вибір елемента із множини Zn для п = 2l, або із Z*p для простого р = 2l + l3 Для цього випадкова двійкова послідовність r довжини l просто розглядається як двійковий запис елемента такої множини.
Щоб отримати випадковий елемент із Zn для довільного п, можна вибрати випадковий елемент х із Z2l, де l = [Iog2 п], і якщо х < п, то використовувати цей елемент, якщо ж х > п, то вибір слід повторити ще раз. Внаслідок цієї процедури буде отримано х  Zn з ймовірністю
Zn з ймовірністю 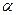 > 1/2. Зрозуміло, що в разі невдачі повторювати вибір доведеться не надто довго. Справді, ймовірність того, що х попаде в Zn лише за i-тим разом, дорівнює (1 —
> 1/2. Зрозуміло, що в разі невдачі повторювати вибір доведеться не надто довго. Справді, ймовірність того, що х попаде в Zn лише за i-тим разом, дорівнює (1 — 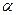 )i-1
)i-1 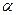 , а математичне сподівання кількості повторень процедури до першого успішного вибору дорівнює
, а математичне сподівання кількості повторень процедури до першого успішного вибору дорівнює
l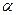 + 2(1 -
+ 2(1 - 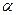 )
) 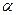 + 3(1 -
+ 3(1 - 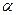 )2
)2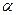 + 4(1 -
+ 4(1 - 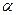 )3
)3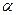 + …=1/
+ …=1/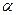 < 2.
< 2.
Таким же чином проводиться вибір випадкового елемента із Z*p для довільного простого р. Щоб вибрати випадковий елемент з множини Z*pq, де р і q прості, можна скористатися наслідком II. 2. 13 з Китайської теореми про остачі. Згідно із ним, досить вибрати x1 і x2 — випадкові елементи множин Z*p і Z*q, і обчислити х  Zpq, для якого х1 = х modp і x2 = x mod q. Такий елемент x рівномірно розподілений на Z*pq.
Zpq, для якого х1 = х modp і x2 = x mod q. Такий елемент x рівномірно розподілений на Z*pq.
Менш вишуканий, але простіший і ефективніший для великих р і q спосіб породження випадкового елемента з Z*pq є таким. Вибираємо випадковий елемент х з Zpq і перевіряємо, чи він ділиться на якесь із чисел р і q. Якщо ні, то х  Z*pq, що нам і потрібно, якщо ж ділиться, то процедуру вибору повторюємо ще раз. Ймовірність того, що вибір буде успішно здійснено за один раз, дорівнює ф(pq)/pq = (1 - 1/р)(1 - 1/q)
Z*pq, що нам і потрібно, якщо ж ділиться, то процедуру вибору повторюємо ще раз. Ймовірність того, що вибір буде успішно здійснено за один раз, дорівнює ф(pq)/pq = (1 - 1/р)(1 - 1/q)
Цей спосіб добрий також тим, що він придатний для породження випадкового елементу множини Z*n для довільного п. А саме, вибирається випадковий елемент ж з Zn і обчислюється НСД(x,п). Якщо останній дорівнює 1, то вибір здійснено, а інакше вибір слід повторити. Ймовірність того, що вибір буде успішно зроблено за один раз, дорівнює ф(п)/п. Оцінимо, наскільки малою є ймовірність того, що елемент із Z*n все ще не буде вибрано упродовж 6 k ln ln n повторень процедури вибору. Ця ймовірність дорівнює (1 - ф(п)/п)6klnlnn. За твердженням II.2.15, ф(п)/п > l/(6lnln n) при великих п. Отже, ймовірність, яку ми оцінюємо, обмежена зверху величиною (1 — l/(61nlnn))6klnlnn яка, у свою чергу, не перевищує e-k за нерівністю В.4. Підсумовуючи, бачимо, що з високою ймовірністю (наскільки високою, залежить від нашого вибору константи k) випадковий елемент х з Z*n можна вибрати в результаті не більше, як
6 k ln ln n незалежних виборів випадкового елемента х з Zn і перевірки умови НСД (х,п) = 1.
У цьому контексті доречно згадати класичний результат Діріхле. Нехай х — випадковий елемент із множини Zn, де п також вибрано випадковим чином в діапазоні від 1 до N. Тоді ймовірність того, що НСД(x,п) = 1 при зростаючому N прямує до 6/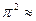 0.6 (див. вправу 3.9).
0.6 (див. вправу 3.9).
ВПРАВИ
3.1. Припустимо, що ймовірнісний алгоритм А розв'язує задачу П з ймовірністю помилки 1/2 — е, де 0 < е < 1/2 (помилка не обов'язково однобічна!). Припустимо також, що кожна індивідуальна задача масової задачі П має єдиний розв'язок — такими є, зокрема, всі задачі обчислення і розпізнавання. Розглянемо такий спосіб зменшення ймовірності помилки. Нехай алгоритм Аt викликає алгоритм А як підпроцедуру непарну кількість разів t, щоразу із незалежним вибором випадкової послідовності бітів. На вихід алгоритм Аt подає результат, що трапився більш ніж у t/2 випадках (якщо ж такого не існує, то видає спеціальний символ #). Довести, що алгоритм Аt розв'язує задачу П з ймовірністю помилки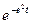 .
.
3.2.Довести, що якщо мова L  А* розпізнається поліноміальним Лас Вегас алгоритмом з ймовірністю невдачі e, то доповнення до неї А* \ L також розпізнається деяким поліноміальним Лас Вегас алгоритмом з такою ж ймовірністю невдачі.
А* розпізнається поліноміальним Лас Вегас алгоритмом з ймовірністю невдачі e, то доповнення до неї А* \ L також розпізнається деяким поліноміальним Лас Вегас алгоритмом з такою ж ймовірністю невдачі.
3.3.Довести, що мова L  А* розпізнається поліноміальним Лас Вегас алгоритмом з імовірністю невдачі е тоді і лише тоді, коли одночасно і L, і її Доповнення A*\L розпізнаються поліноміальними Монте Карло алгоритмами з однобічною помилкою е.
А* розпізнається поліноміальним Лас Вегас алгоритмом з імовірністю невдачі е тоді і лише тоді, коли одночасно і L, і її Доповнення A*\L розпізнаються поліноміальними Монте Карло алгоритмами з однобічною помилкою е.
3.4. Розглянемо різновид ймовірнісного алгоритму, який має доступ до потенційно необмеженої послідовності випадкових бітів r  {0,1} (в ході обчислення може використовуватись лише початковий відрізок г, але як завгодно довгий). За означенням такий алгоритм розпізнає мову
{0,1} (в ході обчислення може використовуватись лише початковий відрізок г, але як завгодно довгий). За означенням такий алгоритм розпізнає мову
L з ймовірністю 1. Це означає, що на кожному вході w для майже всіх r (за винятком множини міри 0 відносно міри Лебега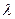 ) алгоритм зупиняється через скінченну кількість кроків, приймаючи
) алгоритм зупиняється через скінченну кількість кроків, приймаючи
w  L і відхиляючи w
L і відхиляючи w 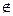 L. Позначимо через t(w, r) кількість кроків алгоритму на вході w з випадковою послідовністю r. Час роботи алгоритму на вході w означимо як інтеграл Лебега
L. Позначимо через t(w, r) кількість кроків алгоритму на вході w з випадковою послідовністю r. Час роботи алгоритму на вході w означимо як інтеграл Лебега  . Довести, що мова L розпізнається у такій моделі за поліноміальний час тоді і тільки тоді, коли вона розпізнається деяким поліноміальним Лас Вегас алгоритмом.
. Довести, що мова L розпізнається у такій моделі за поліноміальний час тоді і тільки тоді, коли вона розпізнається деяким поліноміальним Лас Вегас алгоритмом.
3.5. Цілий вираз над змінними х1,... ,хm означується наступним чином:
· десятковий запис цілого числа є цілим виразом;
· будь-яка із змінних х1,... ,хm є цілим виразом;
· якщо Р і Q — цілі вирази, то (Р • Q), (P + Q), (Р — Q) є цілими виразами.
Наприклад, ((x1 - х2) • (x2 – х3) + х2 • (x1 + х3)) та (х1 • (x1 + х3) - (x1 - х2) • (x1 - х2)) є цілими виразами. Два цілі вирази назвемо тотожними, якщо вони представляють один і той же поліном з цілими коефіцієнтами від змінних х1,... ,хm. Наприклад, два наведені вирази тотожні — обидва представляють поліном, канонічна форма якого — х22 +2 x1х2 + x1х3
Невідомо, чи існує поліноміальний детермінований алгоритм для розпізнавання тотожності двох заданих цілих виразів. Зауважимо, що в загальному випадку цілий вираз не можна звести до канонічної форми за поліноміальний час з тої причини, що його канонічна форма може мати експонен-ційний розмір (як, наприклад, для виразу (х1 + 1)(x2 + 1)... (хm + 1)). Метою вправи є розробити для цієї задачі поліноміальний ймовірнісний алгоритм з однобічною помилкою.
a) Степенем монома  є сума показників i1 + i2 + • • • + іm Степенем полінома називається найбільший степінь монома у його канонічній формі. Довести, що степінь полінома, представленого цілим виразом, не перевищує довжини запису останнього (тобто загальної кількості символів (,),+,-,
є сума показників i1 + i2 + • • • + іm Степенем полінома називається найбільший степінь монома у його канонічній формі. Довести, що степінь полінома, представленого цілим виразом, не перевищує довжини запису останнього (тобто загальної кількості символів (,),+,-, ,х1,... ,хm).
,х1,... ,хm).
b)(J. T. Schwartz, R. Е. Zippel) Нехай F — поле і Н — множина із h елементів цього поля. Нехай р(х1,... ,хm) — поліном в F(х1,... ,хm) степеня d. Нулем полінома р називається такий набір ( )
) Fm, що р(
Fm, що р( ) = 0. Довести, що множина Нm містить щонайбільше dhm-1 нулів полінома р.
) = 0. Довести, що множина Нm містить щонайбільше dhm-1 нулів полінома р.
c)Оцінити час роботи і ймовірність помилки наступного алгоритму розпізнавання тотожності цілих виразів. Нехай на вхід подаються цілі вирази Р і Q від m змінних, кожен довжини щонайбільше п. Випадково і незалежно вибираються m цілих чисел  в межах від 0 до п2 кожне. Вхід приймається, якщо Р(
в межах від 0 до п2 кожне. Вхід приймається, якщо Р( ) = Q(
) = Q( ) і відхиляється інакше.
) і відхиляється інакше.
3.6.Припустимо, що X  Y, де Y -— скінченна множина. Розглянемо такий ймовірнісний експеримент із нескінченної кількості кроків. На t-му кроці з множини Y вибирається випадковий елемент уі, причому вибір здійснюється рівноймовірно і незалежно від попередніх кроків. Позначимо через х перший елемент в послідовності у1 , y2, уз,…., який належить множині X, а через k — номер кроку, для якого вперше уr = х
Y, де Y -— скінченна множина. Розглянемо такий ймовірнісний експеримент із нескінченної кількості кроків. На t-му кроці з множини Y вибирається випадковий елемент уі, причому вибір здійснюється рівноймовірно і незалежно від попередніх кроків. Позначимо через х перший елемент в послідовності у1 , y2, уз,…., який належить множині X, а через k — номер кроку, для якого вперше уr = х  X.
X.
a)Довести, що випадкова величина х рівномірно розподілена на множині X.
ь)Чому дорівнює математичне сподівання випадкової величини k
Нагадування. При розв'язуванні наступних задач слід пам'ятати, що за домовленістю випадковий елемент множини набуває кожне значення з неї з однаковою ймовірністю.
3.7.Нехай m і п — натуральні числа, і х є випадковим елементом множини Zn Довести, що х mod m є випадковим елементом множини Zm тоді і тільки тоді, коли п ділиться на m.
3.8. а) Нехай а — довільний фіксований елемент групи G, a r — випадковий елемент цієї групи. Довести, що їх добуток аr є випадковим елементом групи G.
b)Довести, що добуток випадкових елементів групи є випадковим елементом цієї групи.
3.9.Нехай натуральні числа х і у вибираються випадково і незалежно в діапазоні від 1 до N. Довести, що ймовірність події НСД (х, у) = 1 дорівнює
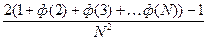
Зауваження. При N 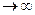 останній вираз прямує до
останній вираз прямує до 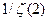 , де
, де 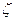 (z) — дзета функція Рімана, яка буде означена у пункті IV. 2. 6. Доведення цього факту можна знайти у [ІЗ, розділ II, вправа 21]. Справедлива також рівність
(z) — дзета функція Рімана, яка буде означена у пункті IV. 2. 6. Доведення цього факту можна знайти у [ІЗ, розділ II, вправа 21]. Справедлива також рівність 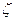 (2) =
(2) =  /6 (див. напр. [15]).
/6 (див. напр. [15]).
ЛЕКЦІЯ 10
| <== попередня сторінка | | | наступна сторінка ==> |
| Прямолінійні програми | | | Арифметика II |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |