• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Прямолінійні програми

Алгоритми та їх складність

Розділ III.

Програмістська практика добре розрізняє алгоритми швидкі та повільні. Ці характеристики вкрай важливі для криптографії. З одного боку, користувачі криптосистеми повинні володіти швидкими алгоритмами шифрування та дешифрування, а з іншого — їх суперник не повинен мати швидкого алгоритму розкриття криптотексту без знання ключа. В ідеалі, суперник не має швидкого алгоритму розкриття не тому, що йому бракує хисту додуматись до такого алгоритму, а тому, що останнього взагалі не існує — всі алгоритми зламу криптосистеми є повільними.

Наявність швидкого алгоритму для розв'язання певної задачі доводиться безпосереднім пред'явленням такого алгоритму. При цьому алгоритм може бути заданим неформальним інтуїтивно прийнятним описом, який, як правило, нескладно записати як програму у будь-якій з існуючих мов програмування. Відсутність же швидкого алгоритму для задачі є фактом більш фундаментального характеру, доведення якого вимагає глибоких математичних методів. Галуззю математики, що займається подібними питаннями, є теорія складності. Цей розділ нашого курсу присвячений концепціям теорії складності, на яких буде грунтуватись подальший виклад алгоритмічних задач теорії чисел, що на них базується сучасна криптографія.

2.1. Означення моделі. Поняття прямолінійної програми можна вводити для довільної алгебраїчної структури. Ми зробимо це для кільця з одиницею. Елементарними операціями будуть множення та додавання в кільці.

Нехай задані наступні об'єкти.

· Символ 1, який називається символом предметної константи і позначає одиницю кільця.

· Алфавіт X = {х₁,...,х_m}, елементи якого називаються вхідними змінними.

· Алфавіт Z = {z_1,.. .,z_l}, елементи якого називаються службовими змінними.

· Три символи операцій •, +, -, для множення, додавання та віднімання.

Прямолінійною програмою називається послідовність із l слів у алфавіті
X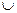Z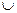{1, •, +, —, =}, в якій i-те слово має вигляд z_s = z'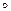z", де 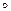є одним із символів операцій, a z', як і z", є або символом предметної константи, або вхідною змінною, або однією із службових змінних z₁,..., z_i-1.

Слова, з яких складається прямолінійна програма, називаються її командами. Зауважимо, що кожна команда виконує операцію над операндами, які можуть бути лише результатами виконання попередніх команд. Кількість команд прямолінійної програми, яку ми позначили через l, називається її довжиною або складністю. Кількість команд множення називається мультиплікативною складністю, а додавання та віднімання — адитивною складністю програми.

Припустимо, що в нас є прямолінійна програма, і нехай R — деяке кільце з одиницею. Кожна команда прямолінійної програми визначає деяку функцію f : R^m R, яка, є поліномом від змінних х₁,...,х_m. Справді, перша команда задає поліном вигляду 1, x_j ± 1, x_j ± x_i, або x_j x_i. Кожна наступна команда задає функцію, що є добутком, сумою або різницею функцій, визначених якимись із попередніх команд, функцію F : R^m R^k розглядаємо як набір k функцій-проекцій f_j : R^m R, де F(х₁,...,х_m) = f₁ (х₁,...,х_m),.., f_k (х₁,...,х_m). Прямолінійна програми обчислює функцію f_j, де 1 j k, визначається деякою командою цієї програми. Складністю обчислення функції F прямолінійними програмами називається найменша довжина прямолінійної програми, що обчислює F. Подібно означуються мультиплікативна та адитивна складності функції.

Приклад 2.1. Функція F(x) = х⁴ + x² в будь-якому кільці обчислюється такою програмою:

z₁ = xx

z₂ = z₁x

z₃ = z₂x

z₄ = z₃+z₁

Отже, складність цієї функції не перевищує 4. Насправді вона менша, тому що для обчислення функції є коротша програма:

z₁ = xx

z₂ = z₁+1

z₃ = z₁z₂

2.2. Піднесення до степеня. Розглянемо задачу обчислення функції f(x) = x^d у довільному кільці. Безхитрісна прямолінійна програма для цієї функції має складність d — 1:

z₁ = xx

z₂ = z₁x

z₃ = z₂x

...

z_d-1 = z_d-2x

У подальших розділах неодноразово виникатиме задача

ПІДНЕСЕННЯ ДО СТЕПЕНЯ ЗА МОДУЛЕМ n

Задано: xZ_n, . dN

Обчислити: x^d mod n.

Завжди можна вважати, що d < n. Інакше можна скористатися теоремою Ойлера, щоб понизити показник. Якщо ми використаємо для розв'язання цієї задачі наведену вище прямолінійну програму (з множенням в кільці Zn), то отримаємо експоненційний алгоритм. Справді коли d не набагато менше, ніж п, то довжина входу має порядок logn а кількість операцій множення має порядок п.

На щастя, є значно ощадніший алгоритм, який був відомий ще до нашої ери в Індії. Ми називатимемо його бінарним методом. Опишемо цей метод у вигляді прямолінійної програми для обчислення функції f(x) = х^d.

Подамо показник d у двійковій системі числення: d = (d_i . . .d₁d₀)₂ де d_i {0,1} і d = 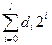Для спрощення запису дозволимо одній команді програми виконувати до двох множень і покладемо z₀ = 1. Тоді i-та команда задається так:

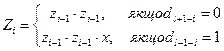
Всього команд l + 1. Результатом виконання останньої є

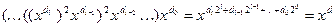
Всього витрачається l+2l21og2d множень (множення першої команди не є необхідним — вона включена для однорідності. Наведену прямолінійну програму можна легко конвертувати в алгоритм у сенсі пункту 1.2, чи в програму на будь-якій мові програмування, що розв'язує задачу піднесення до степеня за модулем п.

ВПРАВИ

2.1.Скласти прямолінійну програму для обчислення в будь-якому кільці загального многочлена степеня п:

f(x,x₀, x₁, . . . , x_n) = x_n xⁿ + x_n-1 x^n-1 + ... + x₁ x + x₀.

a)Реалізувати обчислення безпосередньо за канонічною формою.

b)Реалізувати обчислення за схемою Горнера.

Порівняти складність програми в першому і другому випадках. (Доведення оптимальності схеми Горнера див. в [35] або [7, розділ 12].)

2.2.Довести, що функцію f : Z² Z, задану співвідношенням f(x₁, x₂) = НСД(x₁, x₂), не можна обчислити ніякою прямолінійною програмою.

2.3.Використовуючи бінарний метод, написати прямолінійні програми для обчислення функцій а) х³² , b) х³¹ , с) х²¹ .

ЛЕКЦІЯ 9

Читайте також:

1. II. Вимоги до складання паспорта бюджетної програми
2. Алгоритм створення тренінгової програми
3. Анімаційні програми
4. Антивірусні програми
5. Важливою складовою економічної політики 60-х рр. була реалізація програми “нових рубежів” президента Дж. Кенеді.
6. Визначення змінних програми.
7. Виконання програми - реалізація мови програмування
8. Вікно програми КОМПАС-ГРАФІК
9. Демо режим програми
10. Державні молодіжні програми в Україні
11. Державні програми щодо попередження бездоглядності та безпритульності дітей.
12. Діагностика виробничої програми підприємства

Переглядів: 585