• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тестування простоти

Цей параграф присвячено задачі

Тестування простоти

Задано: п N.

Розпізнати: чи п просте число ?

Алгоритми розв'язування цієї задачі називаються тестами простоти. Якщо алгоритм приймає вхід п, то кажуть, що п проходить або витримує тест.

Перший тест простоти був винайдений понад два тисячоліття тому Ератосфеном з Александрії і називається ситом Ератосфєна. Точніше, сито Ератосфєна — це процедура, яка укладає список всіх простих чисел в межах від 1 до заданого п. Коли початковий відрізок простих чисел вже знайдено, наступне просте визначається за таким критерієм: натуральне число є простим тоді і лише тоді, коли воно не ділиться на жодне із передуючих йому простих чисел. Наступний елементарний приклад тесту простоти спирається на ту ж ідею і вимагає часу не більше, ніж просіювання через сито Ератосфeна.

Вхід: п > 1.

Присвоюємо змінній l значення 2.

· Якщо l > [п/2], то закінчуємо роботу і приймаємо вхід (тобто стверджуємо, що п просте).

· Якщо l [п/2] і l | п, то закінчуємо роботу і вхід відхиляємо (зауважимо, що при цьому знайдено перший простий дільник числа п).

· Якщо l [п/2] і l |- п, то збільшуємо l на 1 і вертаємось до виконання того ж умовного оператора.

Однак оцінювання часу роботи дає невтішний діагноз — описаний алгоритм експоненційний. Якщо вхід п є складеним числом, то перевірка цього може й не зайняти багато часу. Скажімо, якщо п > 2 парне, то це з'ясується вже на першому кроці. Але якщо вхід п є простим, то алгоритм змушений виконати [п/2] — 1 крок для кожного l від 2 до [п/2], а це число є експонентою від довжини входу (див. обговорення на стор. 93).

Насправді можна обмежитись [] кроками, позаяк якщо п має нетривіальний дільник l, то мусить мати і нетривіальний дільник, що не перевищує (або сам l, або п/l). Це зауважив близько 1202 року Леонардо Пізанський, знаний як Фібоначчі. Втім, пришвидшений таким чином алгоритм залишається експоненційним. Наступне пониження оцінки часу, необхідного для тестування простоти, було зроблене лише у 1974 році в роботі [113], де запропоновано алгоритм із оцінкою часу O(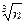). Зазначимо, що цей алгоритм теж не тільки визначає, що число складене, а й знаходить його дільник.

Найкращий з існуючих детермінований алгоритм розроблено у [66]. Він розпізнає простоту за час O((logn)^clogloglogn) для деякої константи с. Алгоритм з такою оцінкою часу роботи називають квазіполіноміальним. Що важливо, цей алгоритм є ефективним на практиці і реально розпізнає простоту чисел, які мають 100 цифр у десятковому записі.

Поліноміальних алгоритмів тестування простоти сьогодні невідомо.

ЛЕКЦІЯ 12

2.1. Ймовірнісний тест Соловея-Штрассена. Ймовірнісний тест простоти був винайдений у [144]. Він є поліноміальним і має однобічну помилку. Цей тест опирається на

Твердження 2.1. Для непарного п 3 покладемо

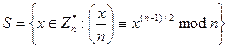
Якщо п складене, то ||S_n|| <. ф(п)/2.

Доведення. За мультиплікативністю символу Якобі (пункт 2 твердження 1.7) S_n є підгрупою мультиплікативної групи . Щоб довести твердження, досить показати, що ця підгрупа є власною. Справді, за теоремою Лагранжа ||S_n|| ділить ||.|| = ф(п), а тому, якщо ці числа не рівні між собою, то ||S_n|| може бути щонайбільше ф(п)/2.

Залишається довести існування елемента у\ S_n. Розглянемо два випадки.

Випадок 1: п вільне від квадратів, тобто у розкладі п = р₁ .. .р_л на прості множники кожне число зустрічається лише один раз.

Виберемо в квадратичний нелишок s за модулем р₁. За Китайською теоремою про остачі в існує у таке, що

y = s(modp₁), у = 1 (modp₂ .. .p_k). (1)

Для такого у за пунктами 4 і 1 твердження 1.7 маємо

Проте у^(n-1)/2 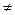— 1 (modn), бо інакше було б у^(n-1)/2 — 1 (modР₂...P_k), суперечність з (1).

Випадок 2: існує просте р таке, що р² | п.

Візьмемо у = 1 + п/р. Зрозуміло, що для кожного q, простого дільника числа п, виконується конгруенція у 1 (modg). Це означає, що у і = 1, останнє за мультиплікативністю символу Якобі.

З іншого боку у^(n-1)/2 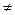— 1 (modn). Справді,

у^(n-1)/2 = (1+n/p) ^(n-1)/2 =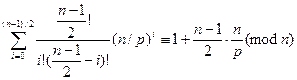

(решта членів у біномі Ньютона кратні п). Отже, якби ліва частина дорівнювала 1 за модулем n, то ми мали б Останнє можливе лише за умови, що р | 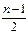що неможливо, бо р|п.

ТЕСТ СОЛОВЕЯ-ШРАССЕНА.

Вхід: п — непарне.

· Вибрати випадкове х таке, що 1 х п — 1.

· Якщо НСД (х,п) 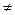1, то припинити роботу з резолюцією "складене", інакше продовжувати.

· Якщо 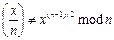, то зупинитись з резолюцією "складене" , інакше зупинитись з резолюцією "просте" .

Коректність. Тест стверджує, що вхід п є простим, для таких і лише таких х, що

НСД(x, n) = 1 i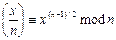

Якщо п просте, то для всіх х від 1 до п — 1 справедливі обидві рівності — перша за означенням простого числа, а друга за критерієм Ойлера. Отож просте п витримує тест з імовірністю 1.

Якщо п складене, то ці дві умови справедливі для всіх х з множини S_n, означеної у твердженні 2.1, і лише для них. Отже, складене п витримує тест з імовірністю, що за твердженням 2.1 не перевищує ф(n)/(2(n-1))<1/2

Таким чином, тест Соловея-Штрассена має однобічну помилку, меншу від 1/2.

Ефективність. Перевірка всіх умов у тесті може бути здійснена ефективно. НСД (х, п) обчислюється за допомогою алгоритму Евкліда, 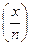— за допомогою алгоритму із пункту 1.2, а — за допомогою бінарного методу з пункту III. 2. 2. Кожен з цих алгоритмів робить O(logn) операцій ділення з остачею чи множення в Z_n. За умови, що ці операції виконуються за час O(log² n), час роботи тесту є O(log³ n)

Ймовірність помилки можна знизити до 2^-k, повторюючи тест k разів згідно із загальною схемою, описаною в пункті III. 3.1. Платою за це буде збільшення часу роботи у k разів.

2.2. Лас Вегас алгоритм. Тест Соловея-Штрассена розпізнає множину простих чисел за поліноміальний час з однобічною помилкою. В [65] запропоновано ймовірнісний поліноміальний алгоритм, що розпізнає з однобічною помилкою множину складених чисел. Як наслідок, для тестування простоти існує Лас Вегас алгоритм (див. вправу III. 3.3).

2.3. Псевдопрості числа. Мала теорема Ферма стверджує, що якщо п — просте число, то для всіх x

x^n-1 1(mod) (1)

Непарне п, яке задовольняє умову (1), але не є простим, називається псєвдопростим числом Ферма або просто псєвдопростим за основою х. Деякі складені числа є псевдопростими за будь-якою основою. Це так звані числа Кармайкла, найменшим з яких є 561 = 3 • 11 • 17.

Критерій Ойлера стверджує, що якщо п — непарне просте число, то для всіх x виконується конгруенція

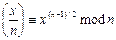(2)

Непарне п, яке задовольняє умову (2), але не є простим, називається псєвдопростим числом Ойлера за основою х.

Оскільки із (2) випливає (1), то кожне псевдопросте число Ойлера за основою х є також псєвдопростим числом Ферма за цією ж основою. Зворотнє твердження неправильне. З нього випливало б, що кожне число Кармайкла є псєвдопростим числом Ойлера за будь-якою основою. Однак чисел з такою властивістю не існує за твердженням 2.1.

Знову припустимо, що п непарне просте. Нехай п — 1 = 2^st, де t непарне. Для елемента х групи розглянемо в цій групі послідовність

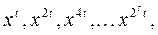
Останній член цієї послідовності дорівнює 1 за малою теоремою Ферма, а кожен попередній є квадратним коренем наступного. Оскільки для простого n є полем, то коренем з 1 може бути лише 1 або — 1. Отже, або вся послідовність складається з одиниць, або має хвіст із деякого числа одиниць, перед якими знаходиться —1. Остання умова рівносильна такій:

або x^t 1 (mod n),

або існує j, 0 j s, таке, що 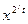—1 (mod n).

Непарне п, де п - 1 = 2^st з непарним t, яке задовольняє умові (3) для x називається сильно псєвдопростим числом за основою х.

Доведення наступних двох тверджень можна знайти в [111, твердження V.1.6] або [55, теорема 17.2], і в [111, твердження V.1.7], відповідно.

Твердження 2.2. З умови (3) випливав умова (2). Отже, сильно псевдопрості числа за основою х є псевдопростими числами Ойлера за цією ж основою.

Твердження 2.3. Непарне складене число п є сильно псєвдопростим за основою х щонайбільше для четвертої частини всіх х таких, що 1х<п.

2.4. Ймовірнісний тест Міллера-Рабіна. На твердженні 2.3 грунтується

Читайте також:

1. Для детального тестування
2. ЕКСПЕРИМЕНТ (ТЕСТУВАННЯ)
3. Етап тестування
4. Метод тестування
5. Методика тестування КІСП аудитором
6. Оскарження або опротестування.
7. Оскарження або опротестування.
8. Перегляд у порядку нагляду рішень, ухвал, постанов у цивільній справі, завдання, суб‘єкти опротестування, суди, які розглядають справи.
9. ПРИКЛАД ОФОРМЛЕННЯ КОНТРОЛЬНОГО ТЕСТУВАННЯ
10. Пробне тестування
11. Протокол тестування
12. Процес тестування

Переглядів: 1134