
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Ймовірнісне криптування
4.1. Ідея.Шафі Гольдвассер і Сільвіо Мікелі [99] запропонували ймовірнісну модифікацію криптографічної схеми з відкритим ключем (див. § 1). їх ідея полягає в тому, щоб зробити алгоритм шифрування Е ймовірнісним.
Ймовірнісний алгоритм шифрування ставить у відповідність повідомленню М не один криптотекст С, а деяку родину криптотекстів cm, причому кожен член 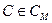 цієї родини вибирається з певною ймовірністю. Іншими словами, для кожного повідомлення М результат роботи алгоритму Е(М) є випадковою величиною, розподіленою на множині cm. Щоб уможливити дешифрування, для будь-якої пари різних повідомлень М1 та М2 відповідні їм множини криптотекстів cmi та cm2 не повинні перетинатися. Більше того, має бути ефективний алгоритм дешифрування, який використовує таємний ключ і за будь-яким
цієї родини вибирається з певною ймовірністю. Іншими словами, для кожного повідомлення М результат роботи алгоритму Е(М) є випадковою величиною, розподіленою на множині cm. Щоб уможливити дешифрування, для будь-якої пари різних повідомлень М1 та М2 відповідні їм множини криптотекстів cmi та cm2 не повинні перетинатися. Більше того, має бути ефективний алгоритм дешифрування, який використовує таємний ключ і за будь-яким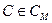 визначає М.
визначає М.
Таку криптосистему вважають надійною, якщо для будь-якої пари повідомлень М1 та М2 однакової довжини l, випадкові величини Е(М1) та Е(М2) неможливо відрізнити одну від одної ніяким ймовірнісним поліноміальним алгоритмом із ймовірністю, вищою за 1/l. Тобто лише з незначною ймовірністю за двома криптотекстами можна визначити, відповідають вони одному й тому ж повідомленню чи різним. Такий рівень надійності в принципі недосяжний для детермінованих систем, у випадку яких пара різних криптотекстів С1 і С2 завжди відповідає різним відкритим текстам М1 і М2. Ймовірнісне криптування вирішує також проблему, зауважену нами на початку пункту 2.4, що детерміноване шифрування не маскує належним чином деякі з повідомлень, наприклад 0 та 1 у випадку системи RSA.
Зупинимось на понятті надійності ймовірнісної криптосистеми з відкритим ключем докладніше. Нехай А — ймовірнісний алгоритм, який завжди подає на вихід одне із двох значень — 1 або 2. Неформально це треба розуміти так, що отримавши на вхід криптотекст С, алгоритм А намагається з'ясувати, що саме має місце, 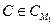 чи
чи 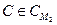 Результат роботи А на вході С позначимо через А(С).
Результат роботи А на вході С позначимо через А(С).
означення 4.1. Ймовірнісну криптосистему з відкритим ключем вважаємо надійною, якщо для будь-якого ймовірнісного поліноміального алгоритму A, для будь-якої пари повідомлень М1 і М2 однакової досить великої довжини l, ймовірності того, що А(Е(Мi) = 1, для і = 1 та i = 2 відрізняються не більш, ніж на 1/l, тобто
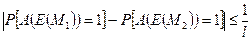 j.
j.
Ймовірність вимірюється за вибором випадкових послідовностей як алгоритмом А, так і алгоритмом шифрування Е.
Таким чином, ймовірнісне криптування можна розцінювати як добре наближення до ідеалу надійності у теоретико-інформаційному сенсі, що досягається для шифру одноразового блокноту. Різниця полягає в тому, що йдеться все ж про надійність в обчислювальному сенсі — це ціна, яку доводиться платити за прийнятну, у порівнянні з шифром одноразового блокноту, довжину ключа.
4.2. Реалізація на основі квадратичності. У [99] ідея ймовірнісного криптування була втілена на основі задачі розпізнавання квадратичних лишків (див. пункти IV.1.2 і IV.4.3).
Введемо позначення Jn для підмножини групи  , що об'єднує елементи х із властивістю
, що об'єднує елементи х із властивістю 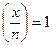 . Нагадаємо, що у випадку коли п = pq є добутком двох різних простих, множина квадратичних лишків Qn є власною підмножиною в Jn. Множина
. Нагадаємо, що у випадку коли п = pq є добутком двох різних простих, множина квадратичних лишків Qn є власною підмножиною в Jn. Множина 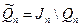 називається множиною псевдоквадратів за модулем п, і має рівно стільки ж елементів, що й Qn (пункт а вправи IV.1.15). Перейдемо до опису криптосистеми.
називається множиною псевдоквадратів за модулем п, і має рівно стільки ж елементів, що й Qn (пункт а вправи IV.1.15). Перейдемо до опису криптосистеми.
Генерування ключів. Вибирають великі прості числа р та q, і обчислюють їх добуток п = pq. Вибирають випадковий псевдоквадрат 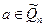 Покладають
Покладають
Відкритий ключ: п, а.
Таємний ключ: р, q.
Шифрування. Двійкове повідомлення М = т1т2...ті, де 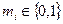 ,перетворюють у криптотекст виглядуС = c1c2... сl де
,перетворюють у криптотекст виглядуС = c1c2... сl де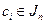 .Для і = 1,...,l елемент ci генерують за допомогою такої ймовірнісної процедури:
.Для і = 1,...,l елемент ci генерують за допомогою такої ймовірнісної процедури:
- вибирають випадковий елемент
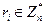 (для кожного і незалежно від всіх інших);
(для кожного і незалежно від всіх інших); - для mi = 0 покладають
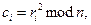
- для mi = 1 покладають
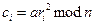 .
.
Дешифрування. За криптотекстом С = с1с2...сl відкритий текст М = m1m2...ml визначають за таким правилом: для і = 1,...,l
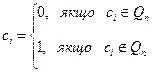
Коректність. Очевидно, що бітові повідомлення mi = 0 у криптотексті відповідає квадратичний лишок сi. Бітові mi = 1 відповідає елемент ci, який є добутком квадратичного лишка і псевдоквадрату, що завжди є псевдоквадратом (див. пункт ь вправи IV. 1.15). Отже, повідомлення М однозначно визначається криптотекстом С незалежно від випадкових виборів елемента ri алгоритмом шифрування.
Ефективність. Зупинимось на виборі псевдоквадрату а, компоненти відкритого ключа. В  вибирають випадковий квадратичний нелишок а1, а в
вибирають випадковий квадратичний нелишок а1, а в 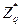 — випадковий нелишок а2 (див. пункт IV. 4.1). Елемент а визначають з умов
— випадковий нелишок а2 (див. пункт IV. 4.1). Елемент а визначають з умов  і
і 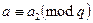 за алгоритмом з Китайської теореми про остачі. Таке а є квадратичним нелишком, бо нелишками є і а1, і a2 — достатньою була б навіть одна з цих причин. З іншого боку, маємо
за алгоритмом з Китайської теореми про остачі. Таке а є квадратичним нелишком, бо нелишками є і а1, і a2 — достатньою була б навіть одна з цих причин. З іншого боку, маємо
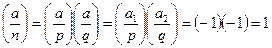
Отже, а є псевдоквадратом. Неважко зрозуміти, що а є випадковим елементом із 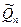 , тобто розподілене на цій множині рівномірно.
, тобто розподілене на цій множині рівномірно.
При дешифруванні треба вміти відрізняти квадратичні лишки від псевдоквадратів. Для цього можна використати зведення задачі розпізнавання квадратичних лишків за модулем n = pq до факторизації числа п з пункту IV.4.3, оскільки співмножники р і q даються таємним ключем.
Приклад 4.2. Візьмемо р = 7 і q = 11. Обчислимо n = 77. Щоб отримати а, вибираємо а1 = 3 і a2 = 2. Для них а = 24. Формування ключів завершено.
Припустимо, що ми хочемо зашифрувати повідомлення НІ.1[1] Його двійковим еквівалентом е 010001 001011 (див. пункт 1.3.1). Почнемо шифрування з першого біта m1 = 0. Нехай r1 = 26. Тоді c1 = 262 mod 77 = 60. Наступним бітом є m2 = 1. Нехай r2 = 41. Тоді c2 = 24•412 mod 77 = 73. Продовжуємо в такому ж дусі. Можливий результат наведено в таблиці.
| i | ||||||||||||
| ri | ||||||||||||
| ci |
Отримуємо криптотекст 60 73 25 53 37 13 23 71 10 15 68 06.
Надійність. Зрозуміло, що задача знаходження біта mi відкритого тексту за компонентою ci криптотексту є задачею розпізнавання квадратичних лишків за модулем n = pq, для якої невідомо жодного ефективного алгоритму (без використання множників р і q, див. зауваження IV.4.5). Для mi = 0 елемент сi є випадковим квадратичним лишком, а для mi = 1 випадковим псевдоквадратом за модулем п. Останнє випливає з пункту ь вправи IV.1.15. На сьогодні невідомо ймовірнісного поліноміального алгоритму, який би відрізняв випадковий квадратичний лишок від випадкового псевдоквадрату за модулем n з імовірністю кращою, ніж 1/logn. Більше того, в [99] показано, що якби такий алгоритм існував, його можна було б перетворити у ймовірнісний алгоритм, який розпізнавав би квадратичні лишки за поліноміальний час. Таким чином, надійність криптосистеми еквівалентна важкості розпізнавання квадратичних лишків за модулем n = pq.
4.3. Реалізація на основі RSA функції. Генерування ключів відбувається таким же чином, як і для системи RSA.
Відкритий ключ: е, п, де n = pq, НСД (е, ф(п)) = 1.
Таємний ключ: d таке, що ed  1 (mod ф(п)).
1 (mod ф(п)).
Шифрування. Двійкове повідомлення М = т1т2...ml, де 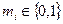 перетворюють у криптотекст виду C = c1.c2...cl, де
перетворюють у криптотекст виду C = c1.c2...cl, де  .Для і = 1,...,l елемент ci генерують за допомогою такої імовірнісної процедури.
.Для і = 1,...,l елемент ci генерують за допомогою такої імовірнісної процедури.
• Якщо mi = 0, то в Znвибирають випадкове парне число xi; якщо mi = 1, то вибирають випадкове непарне xi.
• Обчислюють 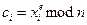 .
.
Дешифрування. За криптотекстом C = c1.c2...cl відкритий текст М М = т1т2...ml визначають за таким правилом: для і = 1,...,l

В [67] доведено, що надійність цієї криптосистеми рівносильна припущенню, що RSA не може бути розкрита поліноміальним алгоритмом.
| <== попередня сторінка | | | наступна сторінка ==> |
| Система Рабіна | | | Система ЕльГамала |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |