• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Система ЕльГамала

ВПРАВИ

4.1. Довести, що якщо в означенні ймовірнісної криптосистеми з відкритим ключем обмеження на ймовірность І/l поміняти на 1/l^c для довільної константи с, то отримаємо рівносильне поняття надійності.

4.2. а) Сформувати відкритий і таємний ключі для системи імовірнісного криптування на основі квадратичності і зашифрувати повідомлення ТАК.

b) Використовуються ті ж ключі, що у прикладі 4.2. Криптотексти 37 64 58 23 71 67 і 25 67 60 15 53 16 76 відповідають одному й тому ж відкритому текстові чи різним?

4.3. Обгрунтувати коректність та ефективність ймовірнісного криптування на основі RSA функції.

Ця ймовірнісна криптосистема була запропонована ЕльГамалом в [88].

Генерування ключів. Вибирають велике просте р, а також число g, 1 < g < р - 1, яке має в мультиплікативній групі великий порядок. В ідеальному випадку g є первісним коренем за модулем р. Числа р і g не є таємницею і перебувають в загальному користуванні. Кожен абонент вибирає собі випадкове число а у проміжку від 1 до р - 1, і обчислює h = g^a mod p.

Відкритий ключ: р, g, h.

Таємний ключ: а.

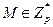Шифрування відбувається блоками. Кожен блок М вважаємо елементом із . Повідомлення перетворюють у криптотекст наступним чином.

Вибирають випадкове число r таке, що 1 ≤ r ≤ р - 1.

Обчислюють С = (с₁, c₂), де

c_І = g^r mod р, с₂ = Мh^r mod p.

Дешифрування. Маючи таємний ключ а і криптотекст С = (с₁,с₂), обчислюють

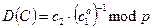
Приклад 5.1. Як і в усіх поперередніх прикладах, ми жертвуємо реалізмом задля простоти обчислень. Нехай р = 23, g = 5, а = 6. Обчислюємо h = 5⁶ mod 23 = 8. Відкритий і таємний ключі сформовано.

Припустимо, що шифрується числова інформація, і потрібно зашифрувати повідомлення М = 7. Нехай вибрано r = 10. Тоді c₁ = 510 mod 23 = 9 і с₂ = (7•8¹⁰) mod 23 = 21. Отримуємо криптотекст С = (9, 21). Що стосується дешифрування, то легко перевірити, що справді D(9,21) = 21•(9⁶)^-1 mod 23 = 7.

Коректність. Перевірка рівності D(C) = М для криптотексту С, отриманого з повідомлення М за допомогою алгоритму шифрування з довільним r, проводиться безпосередньо і залишається читачеві в якості простої вправи. Ідея криптосистеми досить прозора: повідомлення М маскується, набираючи вигляду c₂, а разом з тим посилається підказка с₁, яка дозволяє відтворити М за с₂.

Ефективність. Піднесення до степеня в виконується за допомогою бінарного методу (пункт III.2.2). Як вибрати велике просте р, описано в пункті IV.2.7. Однак наше завдання складніше — слід вибрати також число g. Найкраще було би мати в якості g первісний корінь за модулем р. На жаль, з пункту IV.6.2 нам відомо, що знаходження первісного кореня за заданим р не є легкою задачею. Тому слід ставити завдання генерування пари р, g, для вирішення якого є ефективні процедури (див. пункт IV.6.2, а також вправу VII.2.6).

Надійність. Сформулюємо задачу

Розкриття системи ЕльГамала

Задано: р,g, h, с₁, с₂, де 1 < g < р - 1,

h = g^а mod р, c₁ = g^r mod р, с₂ = Mh^r mod p

для деяких а, r, .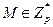

Обчислити: М.

Черговою простою вправою для читача є встановлення того, що ця задача еквівалентна наступній.

Розкриття системи ЕльГамала - 2

Задано: р,g, х,у N, де 1 < g < р - 1, х = g^а mod р,

у = g^ь mod р для деяких а і ь.

Обчислити: z = g^aь mod p.

Для другої задачі очевидно, що вона зводиться до дискретного логарифмування за модулем р. Тому слід виключити ті випадки, у яких логарифмування можна провести ефективно. Зокрема, р слід вибирати так, щоб число р - 1 мало великий простий дільник, інакше суперник зможе скористатися алгоритмом Сільвера-Поліга-Гелмана (пункт IV.7.2). В [80] показано, що у випадку, коли ф(р - 1) має лише малі прості дільники, задача розкриття криптосистеми ЕльГамала еквівалентна дискретному логарифмуванню.

ВПРАВИ

5.1. а) Нехай р = 17, g = 3. Вибрати а і завершити формування ключів. Зашифрувати числове повідомлення 5, вибравши r на власний розсуд.

b) Нехай р = 17, g = З, а = 1. Розшифрувати криптотекст С = (5,15).

5.2. Нехай 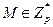— довільне повідомлення, що шифрується в системі ЕльГамала. Припустимо, що g є первісним коренем за модулем р.

a) Чи с₁ розподілене рівномірно на ?

b) Нехай s | (р - 1) і а = (р — l)/s. Скільки значень може набувати c₂? (При малих s приклад поганого вибору а.)

c) Для яких фіксованих а компонента криптотексту с₂ розподілена рівномірно на ? Скільки є таких а? (Приклад доброго вибору а.)

d) Чи c₂ розподілене рівномірно на у припущенні, що таємний ключ а не фіксований, а є випадковим елементом множини ?

5.3. Нехай g є первісним коренем за модулем р.

a) Придумати процедуру, яка ламає систему ЕльГамала, а саме знаходить повідомлення за криптотекстом, у частковому випадку, коли r = (р - 1)/2.

b) Те ж у випадку, коли 3 | (р - 1) і r = (р — 1)/3 або r = 2(р — 1)/3.

c) Позначимо s = (p - 1)/НСД (r,р— 1). Придумати процедуру, яка ламає систему ЕльГамала за час, обмежений поліномом від довжини повідомлення і величин log p та s.

ЛЕКЦІЯ 18

Читайте також:

1. Active-HDL як сучасна система автоматизованого проектування ВІС.
2. II. Бреттон-Вудська система (створена в 1944 р.)
3. IV. Система зв’язків всередині центральної нервової системи
4. IV. УЗАГАЛЬНЕННЯ І СИСТЕМАТИЗАЦІЯ ВИВЧЕНОГО
5. V. Систематизація і узагальнення нових знань, умінь і навичок
6. VI. Система навчаючих завдань для перевірки кінцевого рівня завдань.
7. VI. Система навчаючих завдань для перевірки кінцевого рівня завдань.
8. VI. Узагальнення та систематизація знань
9. VII. Закріплення нового матеріалу і систематизація знань.
10. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
11. Автоматизована система ведення державного земельного кадастру
12. Автоматична система сигналізації

Переглядів: 767