• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Важкооборотні функції

Криптографічні інструменти

Розділ VI.

1.1. Означення і приклади. Які досі, ми розглядаємо функції, областю визначення і множиною значень яких є множина слів у деякому алфавіті. Без втрати загальності обмежимось розглядом двійкового алфавіту. Функція f називається важкооборотною, якщо виконуються такі дві умови.

1 f ефективно обчислюється.

2 Жоден ефективний алгоритм для більшості аргументів 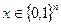невзмозі за образом у = f(x) знайти ніякого елемента х' такого, що f(x’)=y.

Для практика таке означення є цілком зрозумілим. Прикладом може бути функція DES:{0,1}⁶⁴ {0,1І}⁶⁴, якій було присвячено пункт 1.3.4. Ця функція є бієктивною і умова 2 означає просто, що обернена функція не може бути обчисленою ефективно для більшості входів — твердження, яке власне й означає надійність системи DES.

Математична теорія пропонує формалізацію цього, з погляду практика, самодостатнього поняття. Умова 1 легкості обчислення функції f і умова 2 важкості її обернення стають абсолютно строгими. Платою за математичну строгість є те, що ці умови набувають асимптотичного характеру, внаслідок чого стають непридатними для характеризації конкретних скінченних функцій. Втім, така ситуація є типовою для теорії складності, яка попри все добре узгоджується із програмістською практикою.

Одне з можливих означень є таким.

означення 1.1. Функція f називається важкооборотною, якщо

1) f обчислюється за поліноміальний час.

2) Кожен поліноміальний ймовірнісний алгоритм на вході у = f(x) для випадкового 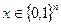знаходить якийсь із проообразів значення у із ймовірністю, що для досить великих п не перевищує 1/п. Ймовірність тут поширюється на випадковий вибір слова 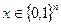і на випадкову послідовність ймовірнісного алгоритму.

З огляду на вступний характер нашого викладу, ми не зупиняємось на нюансах та різновидах означення важкооборотної функції. Зацікавлений читач скеровується до [93].

Ні для якої конкретної функції не доведено, що вона важкооборотна. Але є функції, які гіпотетичне вважаються такими і з успіхом застосовуються на практиці.

функція множення: MULT(x,y) = ху.

Функція визначена на парах натуральних чисел х і у з однаковою кількістю значущих двійкових цифр.

RSA функція: RSA(x, e, m) = (x^e mod m, е, т).

Визначена для m = pq, що є добутком двох різних простих, для е такого, що НСД (е, ф(m)) = 1, і для 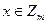. Для фіксованих т і е є бієкцією Z_m на себе, або інакше кажучи, перестановкою множини Z_m (існування оберненого відображення випливає із твердження V.2.2).

функція рабіна (квадратична функція):

SQUARE(x, т) = (х² mod m, m).

Визначена для т = pq і хZ_m, де m є цілим Блюма, тобто р і q — різні прості з властивістю р q 3 (mod 4). Для фіксованого m звуження на Q_m є перестановкою цієї множини (див. вправу V.3.3).

експоненційна функція: ЕХР(х,g,р) = <g^х mod p,g,p>.

Визначена для довільного простого р, первісного кореня g за модулем р, і х . Для фіксованих р і g є перестановкою множини (як легко випливає із вправи IV. 1.4).

Функції RSA і Рабіна є кандидатами у важкооборотні функції із секретом. Крім вищеперелічених умов 1 і 2 ці функції задовольняють ще й третю: володіння деяким секретом (а саме, співмножниками р і q) дозволяє ефективно обчислювати обернені функції. 1.2. Перші застосування. Важкооборотні функції є потужним криптографічним інструментом. На їх основі можна конструювати різні системиймовірнісного криптування. Про це йтиметься далі, а зараз наведемо просте, але ефектне застосування.

Щоб отримати доступ до комп'ютерної мережі, законний користувач повинен засвічити свою особу, ввівши відомий лише йому пароль або гасло (обидва терміни є синонімами, ми надаємо перевагу другому). Несанкціонований користувач, що добре знає систему, при нагоді може знайти в пам'яті місце зі списком гасел легальних користувачів, і надалі користуватися якимось із них. Щоб виключити таку можливість, системі достатньо зберігати у списку не гасло х, а його образ у = f(x) відносно деякої важкооборотної функції f. При введенні га­сла х перевірка рівності f(x) = у здійснюватиметься швидко. З іншого боку, зловмисник, який натрапить на у, не зможе знайти ніякого х'із властивістю f(x') = у завдяки важкооборотності функції f. Як завжди у наших заняттях криптологією, ми цілком припускаємо, що зловмисник знає алгоритм обчислення функції f — це нічим не полегшить його завдання.

Ще одне застосування важкооборотної функції корисне в наступній ситуації. Уявимо собі криптосистему з відкритим ключем для багатьох користувачів на кшталт системи ЕльГамала. Припустимо, що спільною компонентою відкритого ключа є просте число р, яке вибирається і оприлюднюється менеджером центру розподілу ключів. Нечесний менеджер може вибрати р не випадковим чином, а якось так, що отримає можливість читати пошту абонентів своєї мережі (наприклад, він зна­тиме розклад числа р — 1 на прості множники, причому вони будуть малими — цього досить для зламу системи ЕльГамала).

В плані такої загрози абоненти зможуть почувати себе впевненіше, якщо менеджер разом із р пред'явить їм х, для якого f(x) — р, де f -деяка важкооборотна перестановка множини чисел однакової довжи­ни. Виконання цієї додаткової вимоги не є надто обтяжливим. При генеруванні простого числа менеджер вибирає випадкове х і замість тестування його на простоту, тестує f(x). Зауважимо, що f(x) — випадкове число однакової з х довжини, тому ймовірність успішного знаходження простого числа потрібної довжини залишається такою ж. З іншого боку, якщо менеджер добув р якимось підступним способом, то йому буде важко знайти х звластивістю f(x) = р з огляду на важкооборотність функції f.

Ми виходили з припущення, що f є бієкцією. Однак з подібною метою можна використати довільну важкооборотну функцію. Конкретна реалізація цієї ідеї входить в стандарт DSS [122].

1.3. Поняття ядра функції.Повертаючись до означень важкообо-ротних функцій RSA, SQUARE та ЕХР, бачимо, що після фіксації відповідних параметрів, ці функції стають перестановками елементів деякої множини D. Маючи на увазі ці приклади, розглянемо ефективно обчислюване бієктивне відображення f : D —>• D. Водночас розгляне­мо ефективно обчислюваний предикат В : D —>• {0,1} — для кожного х D можна легко обчислити біт В(х). Нехай f(x) = у. Оскільки f — бієкція, то В(х) однозначно визначається елементом у. Однак це не означає, що маючи у, отримати В(х) легко. Якщо немає ефективного алгоритму, який би для більшості елементів х D за заданим значен­ням f(x) давав біт В(х), то предикат В називається ядром функції f (див. малюнок 1).

Малюнок 1. Важкооборотна функція / і її ядро В.

Нескладно збагнути, що коли функція f має ядро, то вона важкооборотна. Справді, якби був ефективний алгоритм для обчислення оберненої функції f^-1, то В(х) було би легко отримати з у композицією алгоритмів для обчислення f^-1 і В.

Тепер дамо формальне означення. Нехай D_n — послідовність множин, для якої п — [log||Dn||]. Нижче поліноміальна обчислюваність означає можливість обчислення за час, обмежений поліномом від п.

Означення 1.2. Поліноміально обчислюваний предикат В: Dn —> {0,1} називається ядром функції f : Dn —> Dn, якщо будь-який поліноміальний ймовірнісний алгоритм на вході f(x), де х - випадковий елемент із Dn, видає значення В(х) з імовірністю меншою, ніж 1/2+1/n^c, для довільної константи с при досить великих п. Ймовірність береться як за випадковим вибором х, так і за випадковою послідовністю ймовірнісного алгоритму.

По суті, означення говорить, що немає ніякого кращого способу отримати В(х) за f(x), ніж просто взяти навмання випадковий біт.

Для перелічених у попередньому пункті важкооборотних функцій в якості ядра запропоновано такі предикати.

Для функції RSA: Zm —> Zm з фіксованими параметрами е і m, a також для функції SQUARE : Qm —> Qm з фіксованим параметром m, В є предикатом парності, тобто В(х) = 1 для непарних х і лише для них. Для функції ЕХР: —> з фіксованими параметрами р і g предикат В задається співвідношенням

Застосування важкооборотних функцій та їх ядер для генерування послідовностей псевдовипадкових бітів буде описане у пункті 2.3. А в наступному пункті висвітлюється зв'язок цих понять з імовірнісним криптуванням.

1.4. Предикат із секретом і ймовірнісне криптування. Повернемося до малюнка 1, де f -- перестановка множини Dn, а В - її ядро. Вважаємо, що множина D, має природну структуру, а саме, існує поліноміальний ймовірнісний алгоритм, який на вході 1ⁿ = 11...1 (параметр п в унарному записі) видає випадковий елемент х, рівномірно розподілений на Dn. Припустимо, що f — важкооборотна функція з секретом. Прикладом може служити функція RSA на множині Zm (при фіксації параметрів m і е). Розглянемо предикат В': Dn —>{0,1}, заданий співвідношенням В'(у) = Ь(f^-l(y)). З означень важкооборотної функції з секретом і її ядра випливають такі властивості.

1) Будь-який ймовірнісний поліноміальний алгоритм на випадковому вході у Dn видає правильне значення В'(у) з імовірністю не кращою, ніж 1/2 + 1/п^с.

2) Знання секрету дозволяє легко обчислити В'(у) для довільного у D_n

3) Є поліноміальний алгоритм, який, отримавши на вхід слово 1ⁿ і біт ь {0,1}, видає елемент у, рівномірно розподілений на множині {у D_n: В'(у) = ь}.

Остання властивість виконується завдяки тому, що f — бієкція. Алгоритм вибирає випадковий елемент х Dn і якщо В(х) = ь, то подає на вихід у = f(x), а інакше пробує інший випадковий х.

Означення 1.3. Предикат В' із властивостями 1-3 називають предикатом із секретом.

Маючи якийсь предикат із секретом, можна влаштувати ймовірнісне криптування, надійне в сенсі означення V.4.I. Щоб зашифрувати двійкове повідомлення М = m₁...m_i; , для кожного і ≤ l слід вибрати випадковий елемент у_i Dn такий, що В'(у_і) = m_i. Криптотекстом буде послідовність з y₁... у_l. Надійність такої системи ймовірнісного криптування забезпечується завдяки умові 1 вище, причому п виступає параметром надійності. Відкритим ключем цієї криптосистєми є дані, потрібні для специфікації алгоритму з умови 3. Таємний ключ складається із секретних параметрів для обчислення предикату В', яке здійснюється при дешифруванні. Існування цих параметрів забезпечене умовою 2.

Схема ймовірнісного криптування на базі функції RSA із пункту V.4.3 є конкретною реалізацією описаної конструкції.

ВПРАВИ

1.1.Пояснити, чому предикат парності не є ядром для функції ЕХР.

1.2.Для розпізнавання квадратичних лишків за модулем m, де m — ціле Блюма, невідомо поліноміального ймовірнісного алгоритму. Виходячи з припущення, що такого алгоритму не існує, довести, що предикат парності є ядром функції Рабіна.

1.3Позначимо через f_e,m: Zm —> Zm перестановку, яка отримується з функції RSA фіксацією параметрів е та m. Нехай Р(х) = х mod 2 - предикат парності, а предикат Q задається на Zm співвідношенням

Розглянемо відповідні два предикати із секретом:

та

Довести, що задачі обчислення цих предикатів є поліноміально еквівалентними.

1.4.Показати, що розкриття криптосистєми RSA поліноміально зводиться до обчислення предикату В₁ з попередньої задачі. Таким чином, якщо є ефективний спосіб за криптотекстом і відкритим ключем визначати лише один, а саме наймолодший, біт відповідного відкритого тексту, то систему RSA можна зламати. Те ж саме можна сформулювати й так: якщо система RSA надійна, то неможливо визначити навіть один (наймолодший) біт повідомлення.

1.5.Довести надійність схеми імовірнісного криптування на основі предикту з секретом.

ЛІТЕРАТУРА

Про важкооборотні функції, що грунтуються на важкості задач алгебраїчного кодування, можна дізнатися з [52, 93, 136].

Аналіз важкооборотних функцій на предмет виділення їх ядра був проведений у [148, 67] для RSA, у [77, 67] для SQUARE, і у [79] для ЕХР. В цих роботах доведено, що коли перелічені функції є важкооборотними, то відповідні предикати є їх ядрами. У [150] встановлено, що кожна важкооборотна функція має ядро. Значно простішу конструкцію ядра запропоновано в [96].

Ідея використання предикатів із секретом для ймовірнісного криптування з'явилась у [99].

Читайте також:

1. Адвокатура в Україні: основні завдання і функції
2. Алгоритм знаходження ДДНФ (ДКНФ) для даної булевої функції
3. Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції .
4. Аналіз коефіцієнтів цільової функції
5. АРХІВНІ ДОВІДНИКИ В СИСТЕМІ НДА: ФУНКЦІЇ ТА СТРУКТУРА
6. Асимптоти графіка функції
7. Базальні ядра, їх функції, симптоми ураження
8. Базові функції, логічні функції
9. Банки як провідні суб’єкти фінансового посередництва. Функції банків.
10. Банківська система та її основні функції
11. Банківська система та її структура. Функції Центрального банку.
12. Банківська система: сутність, принципи побудови та функції. особливості побудови банківської системи в Україн

Переглядів: 1730