• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Асимптотична нормальність й ЦПТ

У прикладі 11 ми бачили, що для оцінок типа 2Х властивість асимптотичної нормальності відразу виходить з ЦПТ (див. також задачу 6 до лекції 1).

Встановимо асимптотичну нормальність оцінок складнішого вигляду (функцій від сум Хі і сум функцій від Хі).

«Лема 4.Хай функція g така, що 0 ¹ D0g(Х1)< оо. Тоді оцінка являється асимптотика нормальною оцінкою для Eqg(X1) з коефіцієнтом

Вправа.Пригадати ЦПТ й довести лему 4.

Вправа.Одержати рішення задачі 6 (після главьі 1) як слідство леми 4.

3.7 Асимптотична нормальність оцінок виглядуН(д(Х)}
Наступна теорема затверджує асимптотичну нормальність оцінок вигляду

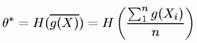
Такне оцінки виходять звичайно при використовуванні методу моментів, при цьому завжди
q= H(Eqg(X1)).

Теорема 9.Хай функція д така, що 0 ^ Е>вд(ХІ)< оо, функція Н непрерьівно дифференцируема в точці а = Евд_{(ХІ), й Н'(а)}^ 0. Тоді оцінка в* = Н(д(Х)) являєшся асимппюпшчески нормальною оцінкою для в = Н(Евд(ХІ))= Н(а) з (Н'(а))2 Овд(ХІ).

Доказ теоремьі 9.Розкладемо Н(д(Х)) в ряд Тейлора в крапці а:

де dn = O((д(Х) — а)²) ® 0 при п —> оо. Останнє вірне, оскільки по ЗБЧ при п —> оо

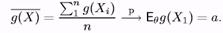
Пригадаємо властивості слабкої збіжності:

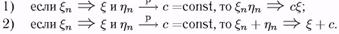
По лемі 4 властивості (1) слабкої збіжності

Звідси (і по властивості (2) слабкої збіжності)

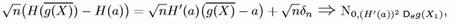
що і вимагалося довести.

Приклад 12.Хай ХІ..., Хп — вибірка обєму п з рівномірного розподілу По,е, де q> 0.

Перевіримо, чи є оцінки 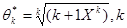= 1,2..., получені методом моментів, асимптотика нормальньми.

Хай д(х)= (k + 1)х, Н(у)= у. Тоді

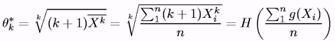
При цьому

Втім, інакше бути не могло за визначенням методу моментів (вірно?). Перевіримо інші умови теореми 9:

кінцева і відмінна від нуля. Функція Н(у) неперервно дифференціальна в крапці а:

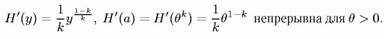
По теоремі 9, оцінка q*. — АНО для qз коефіцієнтом

У тому числі для q1* = 2Х маємо коефіцієнт 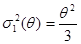(див. приклад 11).

Залишилося зрозуміти, при чому тут порівняння оцінок й що показьшает козффициент асимптотичної нормальності.

Переглядів: 1193