Рішення задачі класифікації нових об'єктів

Переваги методу

Простота використання отриманих результатів.

Рішення не унікальні для конкретної ситуації, можливе їх використання для інших випадків.

Метою пошуку є не гарантовано вірне рішення, а краще з можливих.

Недоліки методу "найближчого сусіда"

Даний метод не створює яких-небудь моделей або правил, що узагальнюють попередній досвід, – у виборі рішення вони ґрунтуються на всьому масиві доступних історичних даних, тому неможливо сказати, на якій підставі будуються відповіді.

Існує складність вибору міри "близькості" (метрики). Від цього заходу головним чином залежить об'єм множини записів, які потрібно зберігати в пам'яті для досягнення задовільної класифікації або прогнозу. Також існує висока залежність результатів класифікації від вибраної метрики.

При використанні методу виникає необхідність повного перебору навчальної вибірки при розпізнаванні, наслідок цього – обчислювальна трудомісткість.

Типові задачі даного методу – це задачі невеликої розмірності по кількості класів і змінних.

За допомогою даного методу розв'язуються задачі класифікації і регресії.

Розглянемо детально принципи роботи методу k-близьких сусідів для вирішення задач класифікації і регресії (прогнозування).

Ця задача схематично зображена на рис. 10.5. Приклади (відомі екземпляри) відмічені знаком "+" або "–", що визначає приналежність до відповідного класу ("+" або "–"), а новий об'єкт, який потрібно класифікувати, позначений червоним кружечком. Нові об'єкти також називають точками запиту.

Наша мета полягає в оцінці (класифікації) відгуку точок запиту з використанням спеціально вибраного числа їх найближчих сусідів. Іншими словами, ми хочемо дізнатися, до якого класу слід віднести точку запиту: як знак "+" або як знак "–".

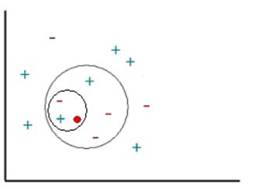
Рис. 10.5. Класифікація об'єктів множини при різному значенні параметра k

Для початку розглянемо результат роботи методу k-ближчих сусідів з використанням одного найближчого сусіда. В цьому випадку відгук точки запиту буде класифікований як знак плюс, оскільки найближча сусідня точка має знак плюс.

Тепер збільшимо число використовуваних найближчих сусідів до двох. Цього разу метод k-ближчих сусідів не зможе класифікувати відгук точки запиту, оскільки друга найближча точка має знак мінус і обидва знаки рівноцінні (тобто перемога з однаковою кількістю голосів).

Далі збільшимо число використовуваних найближчих сусідів до 5. Таким чином, буде визначена ціла околиця точки запиту (на графіці її межа відмічена червоним(сірим) колом). Оскільки в області міститься 2 точки із знаком "+" і 3 точки із знаком "–", алгоритм k-ближчих сусідів привласнить знак "–" відгуку точки запиту.

<== попередня сторінка	\|	наступна сторінка ==>
Лінійний SVM	\|	Рішення задачі прогнозування

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.015 сек.