• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Рішення задачі прогнозування

Далі розглянемо принцип роботи методу k-ближчих сусідів для вирішення задачі регресії. Регресійні задачі пов'язані з прогнозуванням значення залежної змінної по значеннях незалежних змінних набору даних.

Розглянемо графік, показаний на рис. 10.6. Зображений на ній набір точок (зелені прямокутники) отриманий по зв'язку між незалежною змінною x і залежною змінною y (крива червоного кольору). Заданий набір зелених об'єктів (тобто набір прикладів); ми використовуємо метод k-ближчих сусідів для передбачення виходу точки запиту X по даному набору прикладів (зелені прямокутники).

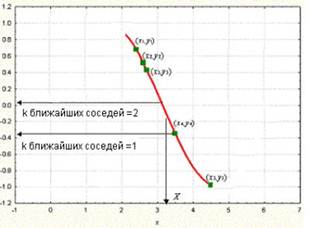
Рис. 10.6. Рішення задачі прогнозування при різних значеннях параметра k

Спочатку розглянемо як приклад метод k-ближчих сусідів з використанням одного найближчого сусіда, тобто при k, рівному одиниці. Ми шукаємо набір прикладів (зелені прямокутники) і виділяємо з їх числа найближчий до точки запиту X. Для нашого випадку найближчий приклад –точка а(x₄; y₄). Вихід x₄ (тобто y₄), таким чином, приймається як результат передбачення виходу X (тобто Y). Отже, для одного найближчого сусіда можемо записати: вихід Y рівний y₄ (Y = y₄).

Далі розглянемо ситуацію, коли k рівно двом, тобто розглянемо двох найближчих сусідів. В цьому випадку ми виділяємо вже дві найближчі до X точки. На нашому графіку це точки y₃ і y₄ відповідно. Обчисливши середнє їх виходів, записуємо рішення для Y у вигляді Y = (y₃ + y₄)/2.

Рішення задачі прогнозування здійснюється шляхом перенесення описаних вище дій на використання довільного числа найближчих сусідів таким чином, що вихід Y точки запиту X обчислюється як середньоарифметичне значення виходів k-ближчих сусідів точки запиту.

Незалежні і залежні змінні набору даних можуть бути як безперервними, так і категоріальними. Для безперервних залежних змінних задача розглядається як задача прогнозування, для дискретних змінних – як задача класифікації.

Передбачення в задачі прогнозування виходить усереднюванням виходів k-ближчих сусідів, а рішення задачі класифікації засноване на принципі "по більшості голосів".

Критичним моментом у використанні методу k-ближчих сусідів є вибір параметра k. Він один з найбільш важливих чинників, що визначають якість прогнозної або класифікаційної моделі.

Якщо вибрано занадто маленьке значення параметра k, виникає ймовірність великого розкиду значень прогнозу. Якщо вибране значення занадто велике, це може привести до сильної зміщуваності моделі. Таким чином, ми бачимо, що має бути вибране оптимальне значення параметра k. Тобто це значення має бути настільки великим, щоб звести до мінімуму ймовірність невірної класифікації, і одночасно, достатньо малим, щоб k сусідів були розташовані досить близько до точки запиту.

Таким чином, ми розглядаємо k як згладжуючий параметр, для якого має бути знайдений компроміс між силою розмаху (розкиду) моделі і її зміщуваності.

Читайте також:

1. Аварійне та довгострокове прогнозування хімічної обстановки
2. Алгоритм прийняття рішення при прийманні сигналів з випадковою початковою фазою
3. Алгоритм розв’язання задачі
4. Алгоритм розв’язання розподільної задачі
5. Алгоритм розв’язування задачі
6. Алгоритм розв’язування задачі
7. Алгоритм розв’язування задачі
8. Алгоритм розв’язування задачі
9. Алгоритм розв’язування задачі
10. Алгоритм розв’язування задачі
11. Алгоритм розв’язування задачі оптимізації в Excel
12. Аналіз інформації та постановка задачі дослідження

Переглядів: 1316