
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Алгоритм розв’язання розподільної задачі
Розв’язання задачі розподілу вагонів під навантаження методом множників, що дозволяють
Попередньо необхідно звести вихідні дані в таблицю (див. табл. 3.1). У цій таблиці рядки відповідають типам вагонів, стовпці – вантажам; останні три стовпці відведені для суми вагонів кожного виду, які використовуються під завантаження, величини надлишків і недостач, а також міток. У кутах клітин записані дійсні технічні норми завантаження pij.
Таблиця 3.1
| Вантаж 1 600 (Bj) | Вантаж 2 | Вантаж 3 | Вантаж 4 | Зайнято вагонів | Ri Надлишок (+) Недостача (-) | Мітка | |
| Вагони 1 типу 30 штук (Ai) | 27 (pij) | ||||||
| Вагони 2 типу 35 штук | |||||||
| Вагони 3 типу 25 штук | |||||||
| lj |
Крок 1. Скласти початковий варіант розподілу вагонів таким чином, щоб кожен вантаж відправлявся в тих вагонах, для яких норма завантаження є максимальною (у разі наявності співпадаючих норм – у менш дефіцитних вагонах). Кількість вагонів кожного типу, що використовуються під завантаження, визначається за формулою xij=Bj/pij (округлити у більшу сторону). Кількість зайнятих вагонів і завантаженого в них вантажу записується у відповідній клітинці через дріб (див. табл. 3.2).
Таблиця 3.2
| Вантаж 1 | Вантаж 2 | Вантаж 3 | Вантаж 4 | Зайнято вагонів | Ri Надл. (+) Нед. (-) | Мітка | |
| Вагони 1 типу 30 штук | +30 | ||||||
| Вагони 2 типу 35 штук | 20/600 | +15 | |||||
| Вагони 3 типу 25 штук | 7/128 | 23/500 | 10/100 | -15 | * | ||
| lj | 1,313 | 1,294 | 1,250 |
Крок 2. Визначити кількість зайнятих вагонів кожного типу 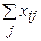 , надлишки (+) і недстачі (-):
, надлишки (+) і недстачі (-):  . Якщо всі Ri³0 розрахунок закінчено – дане рішення є оптимальним.
. Якщо всі Ri³0 розрахунок закінчено – дане рішення є оптимальним.
Крок 3.Класифікувати рядки на надлишкові та недостатні. Недостатніми є всі рядки в яких Ri<0, а також рядки в яких Ri=0 і які відповідають наступній вимозі: поточне значення завантаження в одному зі стовпців дорівнює поточному значенню завантаження в клітинці на перетинанні цього стовпця й одного з недостатніх рядків, при цьому дана клітинка повинна бути зайнятою. Всі недостатні рядки позначаються зірочкою (*) в останньому стовпці. Якщо всі рядки недостатні, то це кінець рішення – вивезти весь вантаж неможливо. Дане рішення забезпечує максимальне вивезення вантажу.
Крок 4. Для кожного стовпця що має xij>0 (зайняту клітинку) у недостатньому рядку визначити відношення 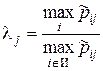 , де у чисельнику узяте максимальне значення завантаження по стовпцю в цілому, а в знаменнику – максимальне значення серед надлишкових рядків. Отримані значення lj записати в нижній рядок.
, де у чисельнику узяте максимальне значення завантаження по стовпцю в цілому, а в знаменнику – максимальне значення серед надлишкових рядків. Отримані значення lj записати в нижній рядок.
Крок 5. Визначити мінімальне значення серед lj: l=minlj
Крок 6. Перетворити матрицю завантажень розділивши всі значення 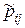 в недостатніх рядках на l. Значення
в недостатніх рядках на l. Значення 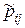 з надлишкових рядків переноситься без змін (див. табл. 3.3).
з надлишкових рядків переноситься без змін (див. табл. 3.3).
Крок 7. В одному з надлишкових рядків матриці знайти клітинку st, для якої величина поточного завантаження дорівнювала максимальній в стовпці. Ця клітинка розглядається як допустима й у неї переноситься додатний обсяг вантажу xst. При цьому необхідно враховувати, що поява нових від’ємних балансів і погіршення використання ресурсів не допускається. Кількість вагонів, що використовуються, визначається за фактичними значеннями завантаження pij.
У табл. 3.3 виконано перерозподіл вантажу 4 в обсязі 100 т з вагонів типу 3 у вагони типу 2. Під цей вантаж необхідно зайняти 13 вагонів типу 2, що менше їх надлишку в 15 одиниць.
Таблиця 3.3
| Вантаж 1 | Вантаж 2 | Вантаж 3 | Вантаж 4 | Зайнято вагонів | Ri Надл. (+) Нед. (-) | Мітка | |
| Вагони 1 типу 30 штук | +30 | ||||||
  Вагони 2 типу
35 штук Вагони 2 типу
35 штук
| 20/600 | 13/100 | +2 | ||||
| Вагони 3 типу 25 штук | 16,8 7/128 | 17,6 23/500 | -5 | * | |||
| lj | 1,050 | 1,035 |
Крок 8. Перейти до кроку 2.
Таблиця 3.4
| Вантаж 1 | Вантаж 2 | Вантаж 3 | Вантаж 4 | Зайнято вагонів | Ri Надл. (+) Нед. (-) | Мітка | |
 Вагони 1 типу
30 штук Вагони 1 типу
30 штук
| +30 | ||||||
 Вагони 2 типу
35 штук Вагони 2 типу
35 штук
| 20/600 | 2/34 | 13/100 | -0 | * | ||
| Вагони 3 типу 25 штук | 23,188 | 16,232 7/128 | 22/466 | 7,727 | -4 | * | |
| lj | 1,111 | 1,249 | 1,333 | 1,143 |
У табл. 3.4 перенесено вантаж 3 з вагонів 3-го типу у вагони 2-го типу. Завантажити можна тільки 2 вагони (мається в надлишку) тобто 34 тонни. Кількість зайнятих вагонів 3-го типу при цьому зменшиться тільки на один.
Таблиця 3.5
| Вантаж 1 | Вантаж 2 | Вантаж 3 | Вантаж 4 | Зайнято вагонів | Ri Надл. (+) Нед. (-) | Мітка | |
  Вагони 1 типу
30 штук Вагони 1 типу
30 штук
| 6/150 | +24 | |||||
 Вагони 2 типу
35 штук Вагони 2 типу
35 штук
| 15/450 | 14,401 | 15,302 7/104 | 7,201 13/100 | |||
| Вагони 3 типу 25 штук | 20,872 | 14,610 7/128 | 15,302 18/396 | 6,955 | |||
| lj |
Отримане рішення є оптимальним тому що всі Ri³0.
Для перевезень використано 66 вагонів.
Читайте також:
- IV. Перевірка розв’язання і відповідь
- Rete-алгоритм
- Алгоритм
- Алгоритм
- Алгоритм 1.
- Алгоритм RLE
- Алгоритм безпосередньої заміни
- Алгоритм Берлекемпа-Мессі
- Алгоритм відшукання оптимального плану.
- Алгоритм Дейкстри.
- Алгоритм Деккера.
- Алгоритм Деккера.
| <== попередня сторінка | | | наступна сторінка ==> |
| Значення й економіко-математичне формулювання розподільної задачі | | | Тема 7. Забезпечення операційної діяльності виробничою |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |