Алгоритм безпосередньої заміни

Один з найбільш загальних алгоритмів переведення чисел визначається правою частиною виразу, що задає правило обчислення кількісного еквівалента числа, записаного у формі (2.2).

Для переведення числа А, заданого в системі числення з основою р, в систему з основою q, необхідно записати А в формі для обчислення кількісного еквівалента (2.2), далі замінити цифри 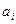і основу р їхніми еквівалентами в системі з основою q, a потім обчислити отримане зображення за правилами арифметики в системі з основою q.

Приклад 2.1. Перевести двійкове число А₂=1101,0101 в десяткову систему числення.

Розв’язання.Використавши формулу (2,2), одержимо

Викладений алгоритм переведення чисел з однієї системи числення в іншу одержав назву алгоритму безпосередньої заміни. Цей алгоритм зручно використовувати у випадку, коли 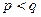, причому q відповідає системі числення, де просто і "звично" виконуються операції додавання і множення (наприклад, у десятковій системі). Для спрощення обчислень при цьому можна побудувати алгоритм обчислень за так званою схемою Горнера, якій у даному випадку відповідає вираз, який легко одержується з формули для кількісного еквівалента числа шляхом багаторазового винесення за дужки:

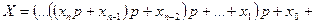
Звідси видно, що алгоритм безпосередньої заміни, власне кажучи, складається з двох алгоритмів, а саме: переведення цілого числа, виконуваного відповідно до рекурентної формули:

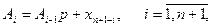
де 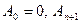- ціла частина вихідного числа в системі числення з основою q; і переведення дробів за рекурентною формулою

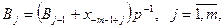
де - дробова частина вихідного числа в системі з основою q. З наведених рекурентних формул випливає, що для одержання 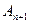необхідно виконати n+1 кроків обчислень, а для одержання 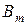- кроків.

На лістингу 1 наведено програму MBZ_c_p_10_Ch(X, p), реалізовану з використанням засобів пакету Mathcad, яка реалізовує алгоритм безпосередньої заміни з використанням схеми Горнера для переведення цілих чисел з системи числення p 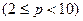в десяткову систему. Тут X задане ціле число, а p – основа числення, в яку потрібно перевести задане число Х, На цьому ж лістингу наведено приклади переведення при різних значеннях p. При цьому результати виводяться як у звичайному вигляді (число А), так і вигляді вектора (вектор Av), компонентами якого є цифри вихідного числа X.

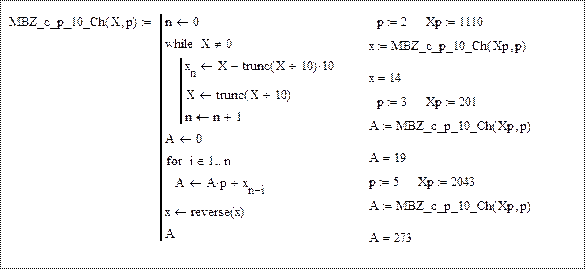
На лістингу 2 наведено програму MBZ_d_p_10_Ch(X,p,m), яка реалізовує схему Горнера для переведення дробових чисел методом безпосередньої заміни з системи числення p 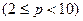в десяткову систему точно або з одержанням m розрядів дробової частини. Робота програми ілюструється прикладами. Результати виводяться як у звичайному вигляді (число В), так і вигляді вектора (вектор Вv), компонентами якого є цифри вихідного числа X.

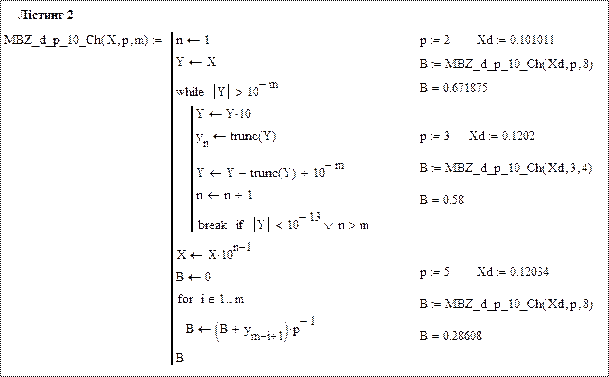
На лістингу 3 наведено програму MBZ_ p_10(X,p,m), яка реалізовує алгоритм для переведення змішаних чисел з використанням схеми Горнера з системи числення p 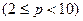в десяткову систему з одержанням m розрядів дробової частини. У цьому випадку спочатку виділяється ціла і дробова частини заданого числа, потім здійснюється переведення цілої і дробової частин і виведення цілої, дробової частин і одержаного числа. Робота програми ілюструється прикладами.

На лістингу 4 наведено програми переведення цілих і дробових десяткових чисел з десяткової системи числення в систему числення з основою р із виведенням результатів у векторній формі. Це дає можливість переводити десяткові числа і в 16-ву систему числення із одним недоліком, що шістнадцяткові числа виводяться в десятковій системі числення. Зауважимо, що при виведенні результатів дробових чисел розряди з нулями в кінці числа не виводяться.

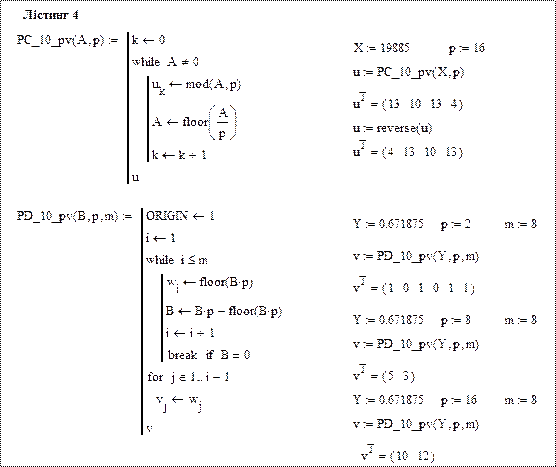
Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Переведення чисел із однієї позиційної системи числення в іншу	\|	Переведення цілих чисел з системи числення з основою q в систему числення p

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.001 сек.