• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Переведення цілих чисел з системи числення з основою q в систему числення p

1⁰. Випадок 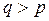. Теоретичною основою алгоритму переведення цілих чисел із системи числення з основою q в систему з основою p у випадку є подання відомого цілого числа 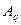, заданого у системі числення з основою q, у вигляді полінома

,

де р – нова система числення, 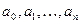– цифри шуканого числа.

Записавши цей вираз за схемою Горнера, одержимо

. (2.3)

Праву частину (2.3) розділимо на основу р. В результаті визначимо перший залишок 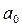і цілу частину 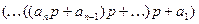. Розділивши одержану цілу частину на р, знайдемо другий залишок . Повторивши процес ділення 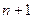раз, одержимо останній залишок 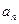, який, за умовою, менший за основу числення р і є старшою цифрою шуканого числа з основою р. Операція ділення виконується в системі числення q, в якій представлене вихідне число. При ручному переведенні цілих чисел за розглянутим алгоритмом запис зручно вести "у стовпчик" (подібно до ручного ділення "у стовпчик").

Приклад 2.2. Нехай 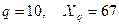. Перевести задане число в системи числення з основами і за вищенаведеним алгоритмом "вручну". Результати переведення наведено в табл.1,2: , .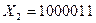

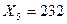Таблиця 2.1 Таблиця 2.2

На лістингу 5 наведено Mathcad-програму для переведення цілих десяткових чисел із десяткової системи числення в систему числення з основою р методом ділення.

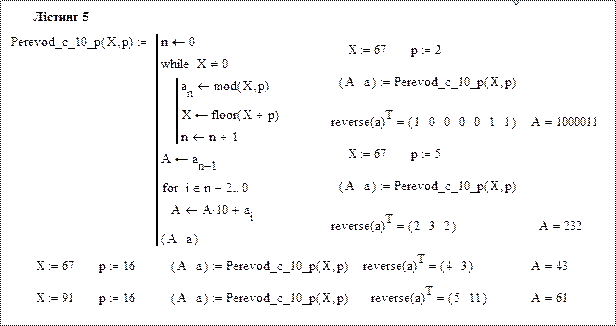
Зауваження. Наведена програма дає можливість переводити із десяткової системи числення в будь-яку позиційну однорідну систему числення, в тому числі і систему числення з основою , наприклад, в шістнадцяткову систему числення. Але, якщо одержувані цифри більші за 10, то правильно формується тільки векторна форма числа, а саме число легко записати в ручному режимі. На лістингу 5 наведено результати переведення десяткових чисел 67 і 91. Оскільки, результатом переведення числа 67 є шістнадцяткове число 43 (обидві цифри меші за 10), то воно переводиться правильно. При переведенні числа 91, одна із остач дорівнює 11 (шістнадцяткова цифра В), тому програмою правильно формується тільки векторна форма число, а саме число потрібно записати вручну А=5В замість А=61, яке видається програмою.

2⁰. Випадок . У даному випадку переведення здійснюється шляхом множення цифри з вагою вихідного числа (тобто, старшої цифри вихідного числа Х) на основу числення р, після чого до одержаного добутку додають наступну, в порядку зменшення ваги розряду) цифру числа Х. Результат одержаної операції множать на р і додають чергову цифру числа Х. Процес закінчується, коли буде додана цифра з вагою . Неважко переконатись, що даний алгоритм є варіантом уже розглянутого вище алгоритму безпосередньої заміни для переведення цілих чисел.

Приклад 2.3. Перевести двійкове число Х=10111001 в десяткову систему за допомогою вищеописаного алгоритму.

Розв’язання. На лістингу 6 наведена цифрову діаграму роботи алгоритму, одержану засобами пакету Mathcad. Реалізація даного алгоритму починається із задання числа А2 у вигляді вектора Аv та початкової суми S=0. Далі виконується послідовність операцій, передбачених вищеописаним алгоритмом.

Це ж саме завдання можна виконати програмними засобами пакету Mathcad. Програми реалізації даного алгоритму наведено на лістингу 7. За допомогою програми Cch_vec(A) здійснюється перетворення числа у вектор, а за допомогою програми PerC_mno(v) здійснюється реалізація алгоритму множення.

Читайте також:

1. I. Органи і системи, що забезпечують функцію виділення
2. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
3. II. Анатомічний склад лімфатичної системи
4. IV. Розподіл нервової системи
5. IV. Система зв’язків всередині центральної нервової системи
6. IV. Філогенез кровоносної системи
7. N – чисельність популяції
8. POS-системи
9. VI. Філогенез нервової системи
10. Автододавання та автообчислення.
11. Автокореляційна характеристика системи
12. АВТОМАТИЗОВАНІ СИСТЕМИ ДИСПЕТЧЕРСЬКОГО УПРАВЛІННЯ

Переглядів: 1817