• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Энергия магнитного поля.

1. Запишите выражение для энергии контура с током.

2. Запишите общее выражение для энергии магнитного поля.

3. Каким образом определяется связь энергии и силы в магнитном поле?

4. Запишите выражение силы Лоренца.

2. Оптика

Оптика - раздел физики, изучающий природу светового излучения, его распространение и взаимодействие с веществом. Световые волны – это электромагнитные волны. Длина волны световых волн лежит в интервале 0,4·10^-6 м ÷ 0,76·10^-6 м. Волны такого диапазона воспринимаются человеческим глазом.

Свет распространяется вдоль линий, называемых лучами. В приближении лучевой (или геометрической) оптики пренебрегают конечностью длин волн света, полагая, что λ→0. Необходимо изучить законы геометрической оптики.

Геометрическая оптика во многих случаях позволяет достаточно хорошо рассчитать оптическую систему. Простейшей оптической системой является линза.

При изучении интерференции света следует помнить, что интерференция наблюдается только от когерентных источников и что интерференция связана с перераспределением энергии в пространстве. Здесь важно уметь правильно записывать условие максимума и минимума интенсивности света и обратить внимание на такие вопросы, как цвета тонких пленок, полосы равной толщины и равного наклона.

При изучении явления дифракции света необходимо уяснить принцип Гюйгенса-Френеля, метод зон Френеля, понимать, как описать дифракционную картину на одной щели и на дифракционной решетке.

При изучении явления поляризации света нужно понимать, что в основе этого явления лежит поперечность световых волн. Следует обратить внимание на способы получения поляризованного света и на законы Брюстера и Малюса.

При изучении темы "Взаимодействие света с веществом" необходимо рассмотреть следующие явления.

Во-первых, при распространении световой волны в веществе скорость зависит от длины волны (или частоты). Это явление называется дисперсией света.

Во-вторых, необходимо изучить такие явления, как поглощение света и рассеяние света.

2.1. Основные формулы

Геометрическая оптика

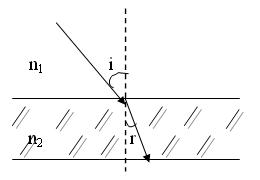Закон преломления света:

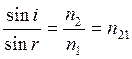
где i – угол падения; r – угол преломления; n₂₁ – относительный показатель преломления второй среды относительно первой; n₁ и n₂ – абсолютный показатель преломле­ния соответственно первой и второй среды.

Предельный угол полного внутреннего отражения при переходе света из среды более оптически плотной в среду менее оптически плотную (n₂<n₁):

i_пр=arcsin ( )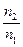

Интерференция

Условие интерференционного максимума (усиления света): на опти­ческой длине пути ∆ укладывается четное число полуволн, т.е. λ/2

∆=± 2k 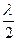(k=0, 1, 2,…).

Условие интерференционного минимума (ослабления света): на оптической длине пути ∆ укладывается нечетное число полуволн:

∆=± (2k + 1) .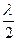

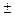
Оптическая разность хода световых лучей, отражённых от двух поверхностей тонкой пластинки (плёнки), по обе стороны которой находятся одинаковые среды: ∆= 2dn cos r , или ,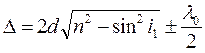

где d – толщина пластинки (плёнки); n – показатель преломления вещества; i₁ – угол падения луча; r – угол преломления света в плёнке (рис.).

Разность хода, равная λ/2, учитывает изменение оптической длины пути световой волны при отражении ее от среды оптически более плотной.

При наблюдении интерференции в проходящих лучах отражение происходит от среды оптически менее плотной, поэтому дополнительной разности хода световых волн не возникает, и оптическая разность хода интерферируемых лучей равна:

∆= 2dn cos r или ∆= 2d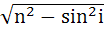

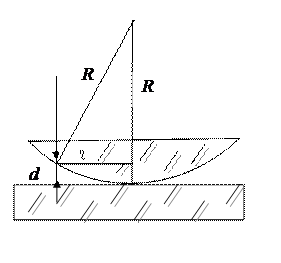Радиусы тёмных колец Ньютона в отражённом свете

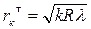(k=0,1,2,3,…).

Радиусы светлых колец Ньютона в отражённом свете:

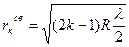(k=0,1,2,3,…).

где k – порядковый номер кольца (k = 0 соответствует центральному тёмному пятну);

R – радиус кривизны линзы;

l – длина световой волны в среде между линзой и пластинкой.

При наблюдении интерференционных колец в проходящем свете расположение светлых и темных колец обратно их расположению в отраженном свете, т.е.

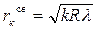
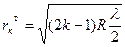
Дифракция света

Положение минимумов освещенности при дифракции на щели, на которую свет падает нормально, определяется условием: a sinj= ±2k 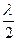, где а – ширина щели; j – угол дифракции.

Условие максимумов освещенности при дифракции на щели: asinj= ±(2k+1) 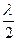, здесь 2k и (2k+1) – число зон Френеля, k – порядок спектра (k = 0, 1, 2, 3).

При дифракции на решетке максимумы интенсивности света наблюдаются в направлениях, удовлетворяющих соотношению (при условии, что свет на решетку падает нормально): dsinj= ± kλ, где d – постоянная дифракционной решетки, k – порядок дифракционного максимума.

Постоянная решетки d связана с числом щелей решетки n, приходящихся на единицу длины решетки, соотношением: d= .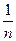

Наибольший порядок максимума при дифракции на решетке определяется соотношением: 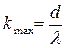. Общее число максимумов, получаемых с помощью дифракционной решетки равно N = 2 .

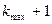Разрешающая способность решетки определяется формулой: 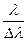=kN, где λ и λ+∆λ – длина волн двух близких спектральных линий, разрешаемых решеткой; N – общее число щелей решетки.

Условие максимумов при дифракции рентгеновских лучей на кристалле описывается формулой Вульфа – Брэгга: 2dsinj=mj, где d – расстояние между атомными плоскостями кристалла (межплоcкостное расстояние); j - угол между пучком рентгеновских лучей и поверхностью кристалла; m- порядок рентгеновского спектра (m = 0, 1, 2, 3).

Поляризация света

Закон Брюстера определяет условие полной поляризации отраженного луча

tgi= 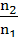=n₂₁. Если отраженный свет полностью поляризован, то справедливо равенство: i+r=90⁰, где i – угол преломления, r – угол падения.

Интенсивность света, прошедшего через анализатор и поляризатор, без учета поглощения определяется законом Малюса: I_a=I_n cos²φ, где I_a, I_n – интенсивности света, соответственно прошедшего через анализатор и через поляризатор; φ – угол между главными плоскостями поляризатора и анализатора.

Тепловое излучение

Энергетическая светимость абсолютно черного тела (коэффициент поглощения α=1) определяется законом Стефана–Больцмана: R_э=σT⁴, где R_э – энергетическая светимость, т.е. энергия, излучаемая в единицу времени с единичной площади на всех длинах волн: R_э= 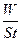; закон Стефана Больцмана для произвольного (серого) тела имеет вид: R_э=ασT⁴, где ρ – коэффициент поглощения (0< α <1); σ – постоянная Стефана- Больцмана; Т – абсолютная температура; W – суммарная энергия излучения по всем длинам волн, испускаемая площадкой S за время t (W=ασT⁴St).

Длина волны λ_m в спектре излучения абсолютно черного тела, на которую приходится максимум спектральной плотности энергетической светимости, определяется первым законом Вина (законом смещения): λ_m= 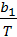, где b₁ – постоянная первого закона Вина.

Максимальное значение спектральной плотности энергетической cветимоcти абсолютно черного тела возрастает пропорционально пятой степени абсолютной температуры (второй закон Вина): r_λ=b₂T⁵, где r_λ – спектральная плотность энергетической светимости, т.е. энергия dW, излучаемая в единицу времени с единичной площади на единичном интервале длин волн (r_λ= 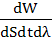= ), b₂ – постоянная второго закона Вина.

Квантовые свойства света. Фотоэффект

Характеристики фотона:

Энергия: ε_ф=hν; масса: m_ф= 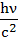; импульс: P_ф= 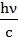= , где h – постоянная Планка; ν= – частота cвета; с - скорость cвета в вакууме.

Условие фотоэффекта описывается уравнением Эйнштейна: hν=A+ 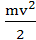, где hν – энергия фотона, падающего на поверхность металла; А - работа выхода электрона из металла; 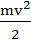– кинетическая энергия фотоэлектрона; m – маcса электрона.

Условие красной границы фотоэффекта: hν₀=A, или h 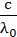=A, где ν₀ – минимальная частота света, при которой еще возможен фотоэффект; с – скорость света в вакууме; λ₀ – максимальная длина волны, при которой еще возможен фотоэффект.

Эффект Комптона

Рассеивание электромагнитного излучения на свободном или слабо связанном электроне, при котором фотон в результате упругого соударения передает частицам часть своей энергии, называется эффектом Комптона. Изменение длины волны при комптоновском рассеянии определяется формулой: ∆λ = 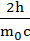sin² , где ∆λ=λ́–λ изменение длины волны; λ́, λ – длина волны соответственно рассеянного и падающего фотона; Θ – угол рассеяния, т.е. угол между направлением падающего и рассеянного фотона; m₀ – масса покоя частицы.

Давление света

При нормальном падении света на поверхность световое давление определяется по формуле: p= 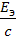(1+с), где 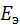– энергетическая светимость поверхности, т.е. плотность потока световой энергии, падающего на данную поверхность: E_э=Nhν, где N – число фотонов, падающих на единицу площади тела в единицу времени; с – коэффициент отражения.

Для идеально отражающей (зеркальной) поверхности коэффициент отражения принимается равным единице, при идеальном поглощении поверхностью (поверхность абсолютно черного тела) - нулю.

Поглощение света

При прохождении света интенсивностью I₀ через слой вещества его интенсивность уменьшается за счёт преобразования энергии световой волны во внутреннюю энергию поглощающего вещества (вещество нагревается) по закону Бугера–Ламберта: 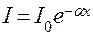, где α – коэффициент поглощения зависящий как от природы поглощающего вещества, так и от длины волны падающего света, х – толщина слоя вещества.

2.2. Примеры решения задач к разделу «Оптика»

Пример № 1. На дифракционную решётку в направлении нормали к её поверхности падает монохроматический свет. Период решётки d=2мкм. Какого наибольшего порядка дифракционный максимум даёт эта решётка в случае красного (l₁=0,7мкм) и в случае фиолетового (l₂=0,41мкм) света?

Дано:

d=2мкм

l₁=0,7мкм

l₂=0,41мкм

k₁, k₂ - ?

Решение. На основании известной формулы дифракционной решётки напишем выражение порядка дифракционного максимума:

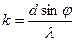, (1)

где d – период решётки; j – угол между направлением на дифракционный максимум и нормалью к решётке; l – длина волны монохроматического света. Так как 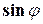не может быть больше 1, то, как это следует из формулы (1), число k не может быть больше 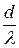, т.е. 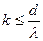. (2)

Подставив в формулу (2) числовые значения, получим:

для красных лучей 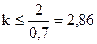, для фиолетовых лучей .

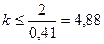Если учесть, что порядок максимумов является целым числом, то для красного света k_max = 2 и для фиолетового k_max = 4.

Ответ:k₁ = 2 и k₂ = 4.

Пример №2. Длина волны, на которую приходится максимум энергии в спектре излучения абсолютно черного тела, 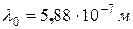. Определить энергетическую светимость (излучательность) 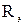поверхности тела.

Дано:

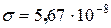Вт/(м²К ⁴)

– ?

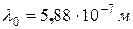
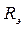Решение. Энергетическая светимость R_э абсолютно черного тела в соответствии с законом Стефана-Больцмана пропорциональна четвертой степени абсолютной температуры и выражается формулой:

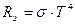, (1) где 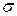– постоянная Стефана-Больцмана; 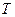– термодинамическая температура.

Температуру Т можно вычислить с помощью закона смещения Вина:

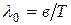, (2)

где в – постоянная закона смещения Вина.

Используя формулы (1) и (2) получим:

. (3)

Подставив числовые значения в формулу (3), произведём вычисления:

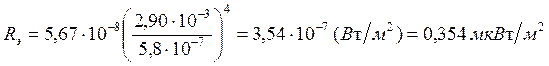
Ответ: R_э=0,354 мкВт/м².

Пример №3. Определить максимальную скорость u_max фотоэлектронов, вырываемых с поверхности серебра: ультрафиолетовыми лучами с длиной волны l₁ = 0,155мкм и g - лучами с длиной волны l₂ = 1пм.

Дано:

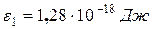
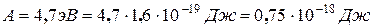
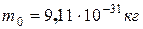
u_max - ?

Решение. Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для внешнего фотоэффекта:

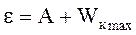; (1)

где e – энергия фотона, падающего на поверхность металла; A – работа выхода электрона с металла;

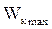– максимальная кинетическая энергия фотоэлектронов.

Энергия фотона вычисляется также по формуле:

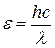; (2)

где h – постоянная Планка; с – скорость света в вакууме; l – длина волны.

Кинетическая энергия электрона может быть выражена или по классической формуле:

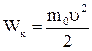; (3)

или по релятивистской формуле:

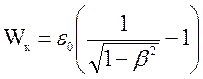, (4)

где ε₀=m₀c² – энергия электрона в состоянии покоя.

Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект: если энергия ε фотона много меньше энергии покоя ε₀ электрона, то может быть применена формула (3), если же ε сравнима по величине с ε₀, то вычисление по формуле (3) приводит к ошибке, поэтому нужно пользоваться формулой (4).

Вычислим энергию фотона ультрафиолетовых лучей по формуле (2):

,

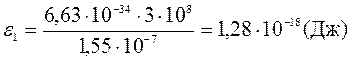или

,

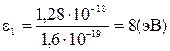Полученная энергия фотона (8эВ) много меньше энергии покоя электрона (0,51МэВ). Следовательно, для данного случая кинетическая энергия фотоэлектрона в формуле (1) может быть выражена по классической формуле (3):

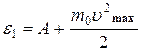
откуда

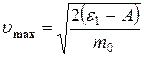. (5)

Подставив числовые значения в формулу (5) , найдём:

.

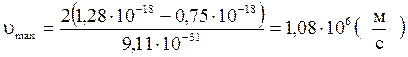Вычислим энергию фотона g – лучей:

,

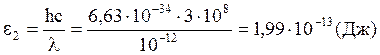или

.

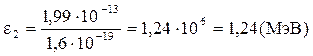Работа выхода электрона (А = 4,7эВ) пренебрежимо мала по сравнению с энергией фотона (e₂ = 1,24МэВ), поэтому можно принять, что максимальная кинетическая энергия электрона равна энергии г-фотона: 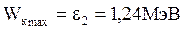. Так как в данном случае кинетическая энергия электрона больше его энергии покоя, то для вычисления скорости электрона следует взять релятивистскую формулу кинетической энергии (4). Из этой формулы найдём:

.

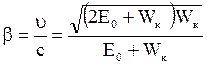Так как 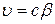и 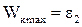получим:

.

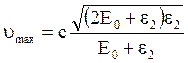Подставим числовые значения величин и найдём искомую скорость:

.

Ответ: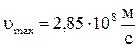

2.3. Базовые задачи для самостоятельного решения

1. На плоскопараллельную пленку с показателем преломления n = 1,33 под углом α = 45° падает параллельный пучок белого света. Определить, при какой наименьшей толщине пленки отраженный свет наиболее сильно окрасится в желтый свет (λ = 0,6 мкм).

Ответ: 133 нм.

2. Плосковыпуклая линза радиусом кривизны 4 м выпуклой стороной лежит на стеклянной пластинке. Определить длину волны падающего монохроматического света, если радиус пятого светлого кольца в отраженном свете равен 3 мм.

Ответ: 0,5 мкм.

3. Плосковыпуклая линза с радиусом сферической поверхности R = 12,5 см прижата к стеклянной пластинке. Диаметры десятого и пятнадцатого темных колец Ньютона в отраженном свете соответственно равны 1 и 1,5 мм. Определить длину волны света.

Ответ: 0,5 мкм.

4. На дифракционную решетку нормально падает монохроматиче­ский свет с длиной волны λ = 600 нм. Определить наибольший порядок спектра, полученный с помощью этой решетки, если ее постоянная d = 2 мкм.

Ответ: 3.

5. На дифракционную решетку длиной l = 1,5 мм, содержащей N = 3000 штрихов, падает нормально монохроматический свет с дли­ной волны λ = 550 нм. Определить: 1) число максимумов, наблю­даемых в спектре дифракционной решетки; 2) угол, соответст­вующий последнему максимуму.

Ответ: 1) 19; 2) 81°54'.

6. Определить число штрихов на 1 мм дифракционной решетки, если углу φ= 30° соответствует максимум четвертого порядка для монохроматического света с длиной волны λ= 0,5 мкм.

Ответ: 250 мм^-1.

7. На дифракционную решетку с постоянной d = 5 мкм под углом i = 30° падает монохроматический свет с длиной волны λ = 0,5 мкм. Определить угол φ дифракции для главного максимума третьего порядка.

Ответ: 53°8'.

8. Определить постоянную дифракционной решетки, если она в первом порядке разрешает две спектральные линии калия (λ₁ = 578 нм и λ₂ = 580 нм). Длина решетки l = 1 см.

Ответ: 34,6 мкм.

9. При прохождении в некотором веществе пути x интенсивность света уменьшилась в 3 раза. Определить, во сколько раз уменьшится интенсивность света при прохождении пути 2х.

Ответ: В 9 раз.

10. Коэффициент поглощения некоторого вещества для монохроматического света определенной длины волны а = 0,1 см^-1. Определить толщину слоя вещества, которая необходима для ослабления света в 2 раза. Потери на отражение света не учитывать.

Ответ: 6,93 см.

11. Угол между главными плоскостями поляризатора и анализатора составляет 30°. Определить изменение интенсивности прошедшего через них света, если угол между главными плоскостями равен 45°.

Ответ: Уменьшится в 1,5 раза.

12. Пучок естественного света падает под углом α = 30° к стеклянной поверхности. Определить показатель преломления стекла, если отраженный луч является плоскополяризованным.

Ответ: 1,73.

13. Определить показатель преломления стекла, если при отражении от него света отраженный луч полностью поляризован при угле преломления 35°.

Ответ: 1,43.

14. Определить, под каким углом к горизонту должно находиться Солнце, чтобы лучи, отраженные от поверхности озера (n = 1,33), были максимально поляризованы.

Ответ: 36°56'.

15. Свет, проходя через жидкость, налитую в стеклянный сосуд (n = 1,5), отражается от дна, причем отраженный свет плоскополяризован при падении его на дно сосуда под углом 41°. Определить: 1) показатель преломления жидкости; 2) угол падения света на дно сосуда, чтобы наблюдалось полное отражение.

Ответ: 1) 1,73; 2) 60°7'.

16. Объяснить, почему в неотапливаемом помещении температура всех тел одинакова.

17. Объяснить, почему открытые окна домов со стороны улиц ка­жутся черными.

18. Чайная фарфоровая чашка на светлом фоне имеет темный рисунок. Объяснить, почему если эту чашку быстро вынуть из печи, где она нагревалась до высокой температуры, и рассматривать в темноте, то наблюдается светлый рисунок на темном фоне.

19. Имеется два одинаковых алюминиевых чайника, в которых до одной и той же температуры нагрето одинаковое количество воды. Один чайник закопчен, а другой – чистый. Объяснить, какой из чайников остынет быстрее и почему.

20. Определить, во сколько раз необходимо уменьшить термодинамическую температуру черного тела, чтобы его энергетическая светимость R_э ослабилась в 16 раз.

Ответ: В 2 раза.

21. Температура внутренней поверхности муфельной печи при от­крытом отверстии площадью 30 см² равна 1,3 кК. Принимая, что отверстие печи излучает как черное тело, определить, какая часть мощности рассеивается стенками, если потребляемая печью мощность составляет 1,5 кВт.

Ответ: 0,676.

22. Энергетическая светимость черного тела Rэ = 10 кВт/м2. Определить длину волны, соответствующую максимуму спектральной плотности энергетической светимости этого тела.

Ответ: 4,47 мкм.

23. Определить, как и во сколько раз изменится мощность излучения черного тела, если длина волны, соответствующая максимуму его спектральной плотности энергетической светимости, сместилась с λ₁ = 720 нм до λ₂ = 400 нм.

Ответ: Увеличится в 10,5 раза.

24. Черное тело находится при температуре T₁ = 3 кК. При остыва­нии тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, изменилась на Δλ = 8мкм. Определить температуру Т₂, до которой тело охладилось.

Ответ: 323 К.

25. Черное тело нагрели от температуры T₁ = 600 К до Т₂ = 2400 К. Определить: 1) во сколько раз увеличилась его энергетическая светимость; 2) как изменилась длина волны, соответствующая максимуму спектральной плотности энергетической светимости.

Ответ: 1) в 256 раз; 2) уменьшилась на 3,62 мкм.

26. Площадь, ограниченная графиком спектральной плотности энергетической светимости r_λ,T черного тела, при переходе от термодинамической температуры Т₁ к температуре Т₂ увеличилась в 5 раз. Определить, как изменится при этом длина волны λ_max, соответствующая максимуму спектральной плотности энергетической светимости черного тела.

Ответ: Уменьшится в 1,49 раза.

27. Объяснить: 1) происхождение радиационной, цветовой и ярко­стной температур; 2) может ли радиационная температура быть больше истинной.

28. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности металла, если фототок прекращается при приложении задерживающего напряжения U₀ = 3,7 В.

Ответ: 1,14 Мм/с.

29. «Красная граница» фотоэффекта для некоторого металла равна 500 нм. Определить минимальное значение энергии фотона, вызывающего фотоэффект.

Ответ: 2,48 эВ.

30. Определить работу выхода А электронов из вольфрама, если «красная граница» фотоэффекта для него λ₀ = 275 нм.

Ответ: 4,52 эВ.

31. Калий освещается монохроматическим светом с длиной волны 400 нм. Определить наименьшее задерживающее напряжение, при котором фототок прекратится. Работа выхода электронов из калия равна 2,2 эВ.

Ответ: 0,91 В.

32. «Красная граница» фотоэффекта для некоторого металла равна 500 нм. Определить: 1) работу выхода электронов из этого металла; 2) максимальную скорость электронов, вырываемых из этого металла светом с длиной волны 400 нм.

Ответ:1) 2,48 эВ; 2) 468 км/с.

33. Фотоны с энергией ε = 5 эВ вырывают фотоэлектроны из металла с работой выхода А = 4,7 эВ. Определить максимальный импульс, передаваемый поверхности этого металла при вылете электрона.

Ответ: 2,96^.10^-25 кг^.м/с.

34. Определить для фотона с длиной волны λ = 0,5 мкм: 1) его энергию; 2) импульс; 3) массу.

Ответ: 1) 2,48 эВ; 2) 1,33^.10^-27 кг^.м/с; 3) 4,43^.10^-36 кг.

35. Определить энергию фотона, при которой его масса равна массе покоя электрона. Ответ выразить в электрон-вольтах.

Ответ: 0,512 МэВ.

36. Давление монохроматического света с длиной волны λ = 500 нм на зачерненную поверхность, расположенную перпендикулярно падающим лучам, равно 0,12 мкПа. Определить число фо­тонов, падающих ежесекундно на 1 м² поверхности.

Ответ: 9,05^.10⁹.

37. На идеально отражающую поверхность площадью S = 5 см² за время t = 3 мин нормально падает монохроматический свет, энергия которого W = 9 Дж. Определить световое давление, оказываемое на поверхность.

Ответ: 667 нПа.

2.4. Контрольные вопросы

Читайте також:

1. Дія на атом зовнішнього магнітного поля. Терема Лармора
2. Електричне поле диполя.
3. Електричний заряд. Електричне поле. Закон Кулона. Напруженість та індукція електричного поля. Принцип суперпозиції електричних полів
4. Енергетична характеристика електричного поля.
5. Зображення електростатичного поля.
6. Квантовые эффекты электромагнитного излучения
7. Магнетного поля.
8. Магнітне коло. Напруженість магнітного поля. Різниця магнітних потенціалів.
9. Методи обробки операційного поля.
10. Напряженность поля. Теорема Гаусса
11. Поняття поля.
12. Поняття поля.

Переглядів: 1407