• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Графове визначення моделі взаємодії об'єктів

Одним з умов побудови моделі взаємодій об'єктів є визначення типів взаємодій об'єктів ОМ між собою в залежності від локального або віддаленого розташування об'єктів щодо один одного і розподіленого середовища. Для перетворення ОМ до моделі взаємодії для кожної вершини графу додається нова додаткова вершина-віддалена, що розташовується на такому більш нижньому рівні ієрархії гілки графу і виконуючої функції взаємозв'язку об'єктів (stub-інтерфейс). Це перетворення призводить до розширеного графа розподілу віддалених об'єктів по мережі U = {W, L}, що взаємодіють.

L – множина дуг-зв'язків віддалених об'єктів;

W = {V' , I} – множина вершин, що включає підмножину V¢= {v₁¢, v₂¢, ... , v_r¢}, r Î k підмножині віддалених об'єктів, розподілених по різних вузлах мережі, і I ={ i₁, i₂ ,... , i_r } – множина об'єктів інтерфейсів для вершин множини V¢, кожний елемент якого визначає інтерфейс stub_j = [ v_j , b (v_j), sp ( v_j )], що складається з елементів:

v_j Î V¢, що розташований у деякому вузлі розподіленого застосування і містить опис зовнішніх змінних, що забезпечують взаємодію між об'єктами множини V';

b(v_j) – оператори передачі повідомлень віддаленій вершині, що визначені на множині зовнішніх змінних EX, розподілених змінних R(V_j¢) або змінних інтерфейсу b (v_j¢) = EX È R;

sp ( v_j) – специфікація інтерфейсу об'єкта – stub, визначена на множині EX È R і задає поводження вершини Vj¢ при посилці повідомлення в мережу.

Stub-інтерфейс j-об'єкта включає: опис усіх змінних, що розташовуються між даним об'єктом і тими об'єктами, із якими він взаємодіє за допомогою протоколів мережного середовища; декларацію початкових значень розподілених змінних; тіло інтерфейсу b(v_j ), що містить оператори викликів віддалених об'єктів, еквівалентних операторам передачі повідомлень по мережі й описаних на множині зовнішніх, рrivate і інтерфейсних змінних; специфікацію об'єкта sp (v_j) у виді формульного визначення розподілених ітерфейсних змінних, що задають поводження об'єкта при передачі повідомлень по мережі.

Властивість віддаленності розподілу об'єктів, а також пов'язаних із ними stub-інтерфейсів відзначається в графі W забарвленням цих вершин (рис.2.3).

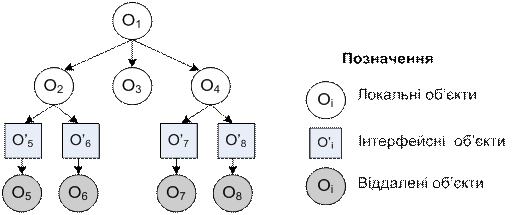
Рисунок 2.3. Приклад розподіленого графу

Граф із виділеними (розфарбованими) віддаленими і інтерфейсними вершинами U = {W, L} будемо вважати розподіленим, а шлях між взаємодіючими об'єктами, у котрому хоча б один з об'єктів є віддаленим – розподіленою схемою (m,п) взаємодії пари об'єктів ( O_i, O¢_i ) і ( O¢_i , O_j ).

У загальному випадку (m,n) – число вхідних і вихідних параметрів повідомлень об'єктів O;

ПрО = (О₁, О₂, ... , О_к) – об'єкти схеми, O_i = < W_i , G> , W_i = (H_i , E_i , h₀ , e_i ) – орієнтований підграф, у котрому Н_i , Е_i – вершини і дуги, h₀ – початкова вершина, e_i – заключна. Підграф повинний задовольняти таким умовам:

1) у вершину h₀ – не ведуть ніякі дуги;

2) із вершини e_i – не ведуть ніякі дуги;

3) H_i \ {e_i } = H_ic È H_i^d, H_ic ÇH_i^d = Æ кожна цільова вершина H_ic об’єднується з інший інтерфейсною вершиною H_i ^d дугою, яка належить множині Е.

Для hÎ H_ic існує єдина дуга (h, h¢)Î E_i із початком у вершині h, для h¢<h_i існує дві дуги в множині Е – (h, h¢). Множина W_i = ( W_ic , W_id) задовольняє умовам:

(1) для будь-якої вершини h Î H_i^d такий, що W_i^d ( h ) = s_i (v_i) у множині повинні існувати ребра (l_j, l_i ) і (l_i, l_j) відповідно;

(2) для будь-якої вершини h¢ Î H_j^d , j = 1,k виконується

W_jd( h ) = il( v_i ) при l £ m , il Î I

Wjd( h ) = ol (vi ) при l £ n,. ol Î O.

(3) для будь-якої вершини h¢ Î H_j¢^d і h¢¢ Î H_j¢¢ ^d, J¢ ¹ J¢¢

W _j¢^d ( h¢ ) Î{ il , ( v¢) , ol¢ (v¢)},

W_j¢ ^d (h¢¢ ) Î { i _l¢¢ (v¢), ol¢¢ ( v¢¢) } , l¢ ¹ l¢¢.

На змістовному рівні множина V¢ являє собою набір методів реалізації віддалених об'єктів, для кожного з них існує елемент множини I , що визначає stub – інтерфейс. Кожний метод реалізації об'єкта задається графом управління, вершини якого розпадаються на вершини розгалуження і перетворення, яким співтавляються оператори передачі повідомлень, що забезпечують зв'язок між об'єктами графа розподілу W. Умова (3) означає, що передача повідомлення призначена тільки одному об'єкту розподілу.

Окремим випадком розподіленої схеми є послідовна (m,n) – схема, для якої в множині Wi немає віддалених об'єктів. Така схема відповідає локальній програмі клієнта і відображає традиційну схему програм.

Переглядів: 774