• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Умовні позначки та інші терміни, що використовуються у фінансових розрахунках

Здійснення різноманітних фі­нансово-економічних розрахунків пов’язано з рухом грошових коштів у часі.

Концепція вартості грошей у часі (Time Value of Money, TVM). Основні теоретичні положення цієї концепції були сформульовані у 1930 році Ірвіном Фішером (Irving Fisher) в роботі «Теорія процента: як визначити реальний доход у процесі інвестиційних рішень» (The Theory of Interest: as Determined by impatience to Spend Income and Opportunity to Invest). Згодом ─ у 1958 році ─ більш розгорнутий механізм цієї концепції був розглянутий Джоном Хиршлейфером (John Hsrshleifer) в роботі «Теорія оптимального інвестиційного рішення» (On the Theory of Optimal Investment Decision). Сутність цієї концепції в тому, що майбутня вартість грошей є більшою за їх теперішню, поточну вартість у зв’язку з альтернативною можливістю їх інвестування, а також впливом факторів інфляції та ризику.

Зміна вартості грошей у часі відіграє ключову роль у фінансових розрахунках. Концепція такої вартості ґрунту-ється на тому, що вартість грошей з часом змінюється під впливом зміни норми прибутку на грошовому ринку, в ролі якої звичайно виступає норма позичкового процента. Враховуючи, що про­цес використання грошей тривалий у часі, на практиці часто не­обхідно порівнювати вартість грошей на початку їхнього «шляху» з вартістю грошей при їхньому поверненні у вигляді майбутнього прибутку або початкової суми разом з прибутком, тощо. Порівнюючи вартість грошових коштів при їхньому вкладенні і повер-ненні прийнято використовувати два основні терміни ─ майбутня вартість грошей і теперішня вартість грошей.

Майбутня вартість грошей — це та сума грошей у яку перетворяться внесені у те­перішній час кошти через пев­ний період часу з урахуванням визначеної ставки процента.

Визначення майбутньої вартості грошей пов’язане з процесом на­рощування вартості, що являє собою поетапне збільшення початкової суми шляхом приєднання до її первісного розміру суми процента. Ця сума процента розраховується за допомогою процен­тної ставки.

Теперішня вартість грошей, або сучасна вартість грошей ─ це початкова сума грошових надходжень або видатків, базова сума (база), з якої починається фінансова операція.

Отже, грошові кошти, що беруть участь у будь-якій фінансовій операції, мають часове навантаження. Вартість (англ. – value) грошей змінюється впродовж часу. Вартість грошей у даний момент, тобто в момент часу, обраний у розрахунку, як теперішній, позначимо символом PV(англ. Present Value – теперішня, сучасна вартість). Вартість грошей у майбутньому, тобто в момент часу, обраний у розрахунку, як майбутнє, позначимо FV (англ. Future Value – майбутня вартість).

Тоді при фінансових розрахунках депозитно-кредитних операцій будемо розуміти під:

PV– сучасна вартість (теперішня вартість), поточна вартість, основна сума, базова величина, внесок (депозит), позика, позичка, сума виданого кредиту, сума вкладеного депозиту, сума боргу та ін.

FV – майбутня вартість, нарощена сума, сума повернення, сума виданого кредиту разом з процентами, сума повернутого депозиту разом з процентами та ін.

(FV ─ PV),різниця між майбутньою та теперішньою вартостями – приріст (нарощення), доход, маржа, процент.

Маржа (від фр. marge ─ край) ─ різниця між ціною купівлі та продажу; плата при укладанні ф’ючерсних контрактів; різниця між процентними ставками по депозитах та виданих кредитах; сума процента від ринкової вартості цінних паперів, яку позичальник повинен сплатити банку при отриманні позики на придбання цих цінних паперів, різниця між ціною купівлі і ціною продажу валюти.

_Приклад 1.7___________________________________

Банк видав кредит у розмірі 100 тис. грн. строком на 1 рік. Клієнт зобов'язаний повернути банку через рік ─ 140 тис. грн.

У даному прикладі PV = 100 тис. грн, FV = 140 тис. грн, доход, отриманий банком у результаті такої кредитної операції, дорівнює: FV ─ PV = 40 тис. грн.

В українській, також як і в російській фінансовій літературі поряд з вказаними використовують інші відповідні PV та FV умовні позначки. Для PV відповідно Р або 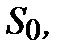для FV відповідно S, показник (FV ─ PV) позначають І ─ (укр. Савлук [5], Бакаєв [1], Михайловська [12], рос. Четыркин [15], Мелкумов [11], Медведев[10], Кутуков [8]). Зрозуміло, що сама суть фінансових розрахунків від виду позначки не змінюється, але, на думку автора, у фінансах назріла необхідність в уніфікації термінології і позначок. Введення в практику фінансового обчислення подвійних англомовних умовних позначок є однією із складових такої уніфікації.

Наступний показник, що є атрибутом фінансових операцій, ─ показник часу, впродовж якого функціонує операція. Цей показник має назву ─ строк,позначимо ─Т. В україномовних фінансових джерелах вживають синонім слова строк ─ термін. Але це слово, при наймі у фінансах, має подвійне значення: ─ 1) слово або словосполучення, що виражає певне поняття; ─ 2) строк, визначений час, що має свої межі, кордони. З метою уникнення подвійного тлумачення, з метою однозначності вживання фінансової термінології будемо завжди іменувати часовий проміжок, впродовж якого діє фінансова операція, строком (Т).

В практиці фінансових розрахунків виникла необхідність визначитись з термінами, вживання яких надзвичайно поширене, це терміни ─ «нарахування» і «нарощення». Іноді ці терміни вважають синонімами, іноді один термін пояснюють за допомогою іншого, іноді вважають, що це слова загального вживання і у фінансах не вживаються, як якісь особливі терміни. Безперечно, це загальномовні слова-терміни, але при використанні їх в розрахунках фінансової направленості наведені терміни набувають додаткових якісно-розрахункових ознак.

Надалі будемо розуміти під терміном «нарощення» ─ часову визначеність розрахунку, а саме ─ направленість розрахунку у часі: від сьогодні до майбутнього (від PV до FV), або від минулого до сьогодні, або від минулого до майбутнього. Часова направленість розрахунків «нарощення» співпадає з направленістю плинності часу.

Визначеність, що є протилежною терміну «нарощення» (за часовою характеристикою), має свій термін ─ дисконтування. Докладніше про дисконтування в Розділах 3, 4, а зараз визначаємо, що «дисконтування» ─ часова визначеність розрахунку, а саме ─ направленість розрахунку у часі: від майбутнього до сьогодні (від FV до PV).Часова направленість розрахунків, які характеризуються як «дисконтування», протилежна за направленість плинності часу.

На відміну від термінів «нарощення» і «дисконтування»термін «нарахування»─ це розрахункова дія, це механізм розрахунку, які (механізм, дія) не пов’язані з часовою направленістю. Механізм розрахунку, що діє «як додавання», «як приєднання» і, в результаті діє «як збільшення», «як зростання», загалом, розуміють у фінансах як безпосередньо ─ нарахування. Але, механізм розрахунку, що діє «як від’єднання», «як зменшення», «як знижка», також механізм розрахунку, тобто, також ─ нарахування. Нарахування, що надає результат «як зменшення» бази, з якої йде розрахунок, в бухгалтерських і податкових розрахунках має назву ─ утримання, але у фінансах розрахунки «на збільшення» і розрахунки «на зменшення» є механізмами розрахунку і узагальнено трактуються ─ нарахування.

Нарахування, ─ це механізм розрахунку, який надає результат або «як збільшення», або «як зменшення» бази, з якої починається нарахування.

Існує ще один важливий показник, що відображає також часову характеристику фінансової операції, його назва: ─ період нарахування процента(running period). Цей показник відіграє ключову роль у фінансових обчисленнях і жорстко пов’язаний з такими показниками, як норма процента або ставка процента. Види ставки процента, ─ процентна ставка та облікова ставка завжди «діють», «працюють» в певних визначених часових межах. Отже, період нарахування процента, ─ це проміжок часу, в межах якого йде зростання (нарощення) або зменшення тієї грошової суми, що фіксується на початку періоду нарахування. Кількісним показником зростання в межах періоду нарахування процента є процентна ставка та облікова ставка в будь-яких їх формах.

Важливим у механізмі фінансових розрахунків є співвідношення між періодом нарахування процента і строком.Варіантів співвідношення чотири.

1-й варіант─ період нарахування процента співпадає зі строком, тобто часова тривалість періоду нарахування і строку рівні між собою.

2-й варіант─ період нарахування процента менше за строк і при цьому тривалість періоду кратна строку, тобто строк має цілу кількість періодів. Наприклад, період нарахування ─ 1 рік, строк ─ 4 роки, отже, кількість періодів нарахування процентів в «кордонах» строку дорівнює 4.

3-й варіант─ період нарахування процента менше за строк і при цьому тривалість періоду не кратна строку, тобто строк має цілу кількість періодів і ще часинку наступного. Наприклад, період нарахування процента ─ річний, строк ─ 4 роки і 4 місяці, отже, кількість періодів нарахування процентів дорівнює 4 цілих і 4/12 (записується так: ).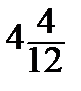

4-й варіант─ період нарахування процента більше за строк. Наприклад, період нарахування процента ─ 1 рік, строк ─ 4 місяці, отже, кількість періодів нарахування процентів дорівнює 4/12 (записується так: ).

Зазначені варіанти накладають свій відбиток на механізм фінансових розрахунків і «породжують» варіанти розрахунків відповідно до варіантів співвідношення між періодом нарахування процента і строком. Також, з’являється новий показник, що показує, скільки разів впродовж строку фінансової операції нараховувалися проценти. Позначимо цей показник символом n.

_________НЕОГОЛОШЕНЕ ПРАВИЛО _________

Як що тривалість періоду нарахування процентів додатково не оговорена, то у фінансах вважається, ЩО ПЕРІОД НАРАХУВАННЯ ПРОЦЕНТІВ ─ 1 РІК. Іншими словами: НАРАХУВАННЯ ПРОЦЕНТІВ ─ РІЧНЕ.

Повертаємось до показників PV та FV та за їх допомогою покажемо у формалізованому вигляді (тобто у вигляді формул) механізм розрахунку показника норми процента та сутність розрахунків ставок процента: ─ процентних ставок і облікових ставок.

Відображення показника «норма процента» у вигляді тотожності полягає в тому, що тотожність стає рівнянням, яке вибудовано у часовому форматі. Те, що стоїть у рівнянні до знака «=» (до знака «дорівнює»), інформує про те, що було в минулому, що вже відбулося і структуроване, як відношення. Те, що стоїть після знака «=», показує те, що є результатом, що є фактом на момент закінчення операцій, операцій які характеризувалися FV та PV. Механізм розрахунку норми процента має такий формалізований вигляд:

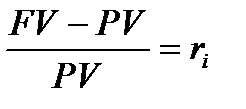, (1.1)

де 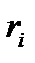─ норма процента (англ. rate of interest).

Розрахунок за формулою (1.1) надає результат, що характеризується як темп норми процента. Якщо показник темпу відобразити у відсотках, будемо мати рівень норми процента. Ще одна особливість формули (1.1). Строк фінансової операції від моменту PV до моменту FV стає періодом для 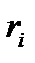, тобто часова тривалість періоду за який розраховано темп або рівень норми процента і тривалість строку ─ це один і той же часовий відрізок (характерна ознака 1-го варіанту співвідношення).

Якщо при відображенні показника «норма процента» часова характеристика за якістю є ─ «від минулого до тепер» і чисельно є такою: те, що було, дорівнює тому, що сталося фактично, то часова направленість процентної ставкиінша: ─ «від сьогодні в майбутнє».

У подальших розрахунках процентна ставка буде позначатися символом «і»(англ. interest rate).

Для відображення рівнянням показника ─ «процентна ставка» тотожність трансформується шляхом її часового форматування, іншими словами ─ структурування тотожності за часовою характерністю, а саме: виділення часового характеру, притаманного процентній фінансовій операції, що і надає тотожності форму рівняння. Те, що стоїть у такому рівнянні до знака «=» (до знака «дорівнює» ─ ліва частина формули), відображає наступне: якщо з моменту початку і впродовж строку фінансової операції будемо використовувати «інструмент що нарощує» розміром «і», то(після знака «дорівнює») будемо в майбутньому мати результат, який розраховується так…(тут іде запис правої частини рівняння з використанням показників FV та PV). Механізм розрахунку ставки процента має такий формалізований вигляд:

─ темп процентної ставки:

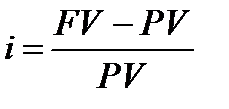, (1.2)

де і ─ процентна ставка;

─ рівень процентної ставки:

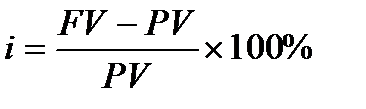. (1.3)

_________НЕОГОЛОШЕНЕ ПРАВИЛО__________

ТЕРМІНИ«РІВЕНЬ ПРОЦЕНТНОЇ СТАВКИ» І «ПРОЦЕНТНА СТАВКА» ВЖИВАЮТЬСЯ У ФІНАНСАХ ЯК СИНОНІМИ. Це пов’язано з тим, що показники вимірювання ставок процента, а відповідно і «процентних ставок», функціонують, ЯК ПРАВИЛО, у відсотках, а показник «рівень процентної ставки» ЗАВЖДИ надається у відсотках.

У фінансах процентна ставка застосовується не лише як інструмент нарощування вартості грошових коштів, а й у ши­ршому сенсі ─ як вимірник ступеня дохідності фінансових або загалом економічних опера­цій. Показник «процентна ставка» з позицій грошової оцінки вказує на очікуваний розмір доходу (прибутку) від вкладеної «у справу» однієї грошової одиниці.

Також, у формулах (1.2) і (1.3) часова тривалість періоду за який розраховано темп або рівень процентної ставки і тривалість строку ─ це один і той же часовий відрізок (характерна ознака 1-го варіанту співвідношення).

Звертаємо увагу, що в формулах (1.1), (1.2) і (1.3) за базу розрахунку береться показник PV ─ сума, яка в часовому вимірі існує на початку фінансової операції, що і є якісною відмінністю процентної ставки від облікової ставки.

Обґрунтування рівняння, яке відображає сутність облікової ставки залишимо поза увагою. Воно подібне до механізму відображення рівнянням показника «процентна ставка». Лише звернемо увагу на відмінність: якщо часова направленість розрахунку з використанням процентної ставки: ─ «від сьогодні в майбутнє», то часова направленість розрахунку з використанням облікової ставки: ─ «з майбутнього до сьогодні».

Якісною ознакою показника «облікова ставка» є віднесення доходу до FV, тобто за базу розрахунку береться сума, яка з часової точки зору очікується в кінці фінансової операції.

У подальших розрахунках облікова ставка буде позначатися символом «d»(від англ. discount rate).

Механізм розрахунку облікової ставки має такий формалізований вигляд:

─ темп облікової ставки:

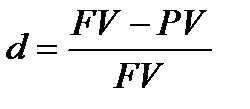, (1.4)

де d ─ облікова ставка;

─ рівень облікової ставки:

. (1.5)

Показник «облікова ставка» з позицій грошової оцінки вказує на очікуваний розмір доходу (прибутку) від одержаної «в кінці справи» однієї грошової одиниці.

_________НЕОГОЛОШЕНЕ ПРАВИЛО__________

ТЕРМІНИ«РІВЕНЬ ОБЛІКОВОЇ СТАВКИ» І «ОБЛІКОВА СТАВКА» ВЖИВАЮТЬСЯ У ФІНАНСАХ ЯК СИНОНІМИ. Це пов’язано з тим, що показники вимірювання ставок процента, а відповідно і «облікових ставок», функціонують, ЯК ПРАВИЛО, у відсотках, а показник «рівень облікової ставки» ЗАВЖДИ надається у відсотках.

_Приклад 1.7_(продовження)_____________________

1. Умови кредитної операції, з якої є можливим розрахунок норми процента.

«Банк видав кредит у розмірі 100 тис. грн. строком на 1 рік. Пройшов рік і клієнт повернув банку 140 тис. грн. Знайти темп і рівень норми процента».

Використовуючи формулу (1.1) темп норми процента дорівнює:

.

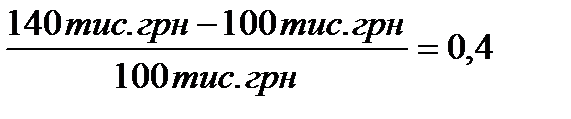Рівень норми процента, або, що одне і теж, норма процента дорівнює:

Нагадуємо, що розрахунок темпу і рівня норми процента є можливим, коли фінансова операція заверши-лася, тому у цьому прикладі під числом 1. умови кредитної операції записано у минулому часі.

2. Умови кредитної операції, з якої є можливим розрахунок процентної ставки та облікової ставки.

«Банк надає кредит у розмірі 100 тис. грн. строком на 1 рік. Згідно угоди, після закінчення року клієнт поверне банку 140 тис. грн. Знайти темп і рівень процентної ставки та облікової ставки».

Використовуючи формулу (1.2) темп процентної ставки дорівнює:

і = .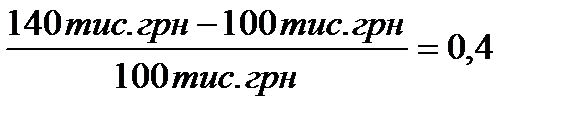

Використовуючи формулу (1.3) рівень процентної ставки, або, що одне і теж, процентна ставка дорівнює:

і =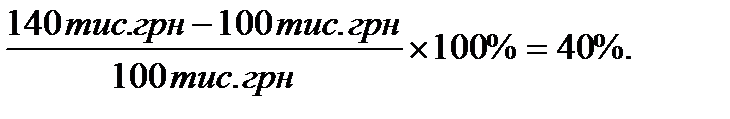

Використовуючи формулу (1.4) темп облікової ставки дорівнює:

.

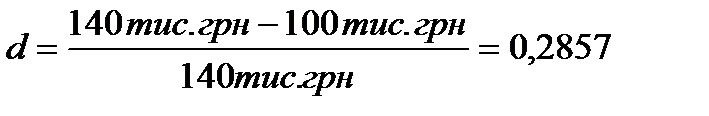Використовуючи формулу (1.5) рівень облікової ставки, або, що одне і теж, облікова ставка дорівнює:

.

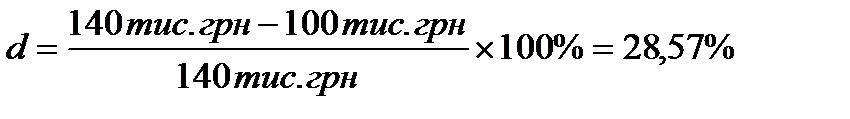Процентна ставка, що дорівнює 40% ─ річна, а також, облікова ставка, що дорівнює 28,57% ─ річна, бо проміжок часу в прикладі дорівнює одному року.

Ще раз звертаємо увагу на відмінність: якщо часова направленість розрахунку з використанням процентної ставки: ─ «від сьогодні в майбутнє», то часова направленість розрахунку з використанням облікової ставки: ─ «з майбутнього до сьогодні».

У подальших фінансових розрахунках важливо розрізнювати та правильно використовувати показники «процентна ставка» й «облікова ставка».

_ _______________________Довідкова інформація_

В математиці запис, в якому є знак «=», має назву ─ рівняння. Рівняння має дві частини, умовно ─ права і ліва, на які його поділяє знак «=».

Для тих, хто давно вивчав математику, нагадаємо метод, за допомогою якого проводиться розв’язування рівнянь: ─ це метод еквівалентних перетворень.

Для розв’язання рівняння важливим є наступні властивості еквівалентності рівнянь.

Якщо обидві частини рівняння помножити або поділити на одне і теж число, яке не є нуль, то будемо мати рівняння, еквівалентне даному.

Якщо будь-який доданок перенести з однієї частини рівняння в іншу, змінивши його знак на протилежний, то будемо мати рівняння, еквівалентне даному.

Якщо обидві частини рівняння піднести до одного і того ж ступеня, або з кожної частини добути один і той же корінь, то будемо мати рівняння, еквівалентне даному.

_Додаткова інформація_________________________

Виникає цікавий результат, якщо рівняння 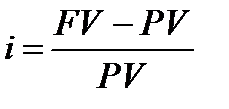(1.2)

(1.2)

перетворити в еквівалентне йому рівняння відносно FV, як невідомої величини.

Зробимо перетворення, використовуючи метод еквівалентних перетворень.

По-перше, помножимо праву і ліву частини рівняння на PV, одержимо:

PV · і = FV ─ PV.

По-друге, перенесемо з правої частини рівняння до лівої показник PV, змінивши при переносі знак , що стоїть при PV з «─» на «+», одержимо:

PV · і + PV = FV.

По-третє, в лівій частині рівняння винесемо PV за дужки, маємо:

PV 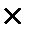( і + 1) = FV , (1.6)

або, що одне і те ж, рівняння (1.2) приймає вигляд:

FV = PV 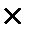(1 + і) . (1.6)

А якщо рівняння 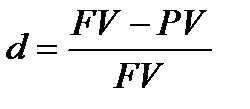(1.4)

(1.4)

перетворити в еквівалентне йому рівняння відносно PV, як невідомої величини, то маємо наступне.

По-перше, помножимо праву і ліву частини рівняння на FV , одержимо:

FV · d = FV ─ PV.

По-друге, перенесемо з правої частини рівняння до лівої показник FV, змінивши при переносі знак , що стоїть при FV з «+» на «─», одержимо:

FV · d ─ FV = ─ PV.

По-третє, помножимо праву і ліву частини рівняння на показник «─1», одержуємо:

FV ─ FV · d = PV.

Четверте, в лівій частині рівняння виносимо FV за дужки і маємо:

FV·(1 ─ d) = PV, (1.7)

або, що одне і те ж, рівняння (1.4) приймає вигляд:

PV = FV 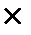(1─ d). (1.7)

Рівняння, подібні (1.6) (1.7) відтепер, будуть часто зустрічатися у фінансових розрахунках.

Читайте також:

1. Алгоритмічна конструкція повторення та її різновиди: безумовні цикли, цикли з після умовою та з передумовою.
2. Амортизація як джерело фінансових ресурсів підприємств
3. Аналіз доцільності фінансових інвестицій у корпоративні права.
4. Аналіз рівня, динаміки та структури фінансових результатів підприємства
5. Аналіз стратегічних альтернатив та визначення оптимальної стратегії формування фінансових ресурсів
6. АНАЛІЗ ФІНАНСОВИХ ЗВІТІВ
7. Аналіз фінансових інвестицій та їх ефективності.
8. Аналіз фінансових коефіцієнтів.
9. Аналіз фінансових результатів діяльності туристичних підприємств
10. Антропометричні параметри людини, які використовуються в ергономіці (см)
11. Аудит фінансових результатів роботи підприємства
12. Аудиторські докази щодо тверджень керівництва у фінансових звітах отримуються безпосередньо в процесі проведення тестів контролю та процедур по суті.

Переглядів: 754