• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розв’язування.

За формулою 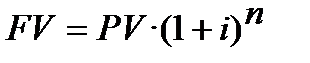розрахунок має вигляд:

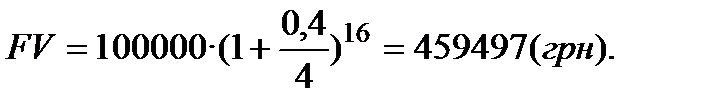
Відповідь: Сума повернення дорівнює 459497 грн.

Поставимо таке питання.

А якою би мала бути в попередній задачі річна ставка, якби нарахування процентів було річне, а не щоквартальне, а сума повернення залишилась би без змін, FV = 459497 грн?

Розрахунок такої ставки стає можливим при розв’язуванні рівняння:

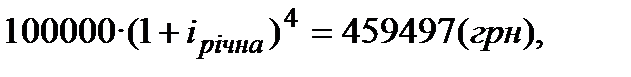
з яког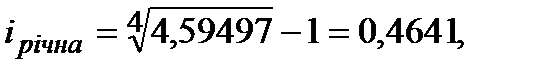о тобто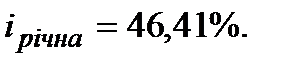

Така річна ставка має назву ─ ефективна ставка.

Ефективна ставка (effective rate) ─ це така річна ставка при річному нарахуванні процентів, що дає той же результат при іншій ставці (теж ─ річній, що іменується номінальною), але при інших періодах нарахування процентів, відмінних від річного нарахування процентів.

В задачі Прикладу 9.1 при складному щоквартальному нарахуванні процентів за ставкою 40% маємо результат FV = 459497 грн. Такий же результат одержуємо при складному щорічному нарахуванні процентів за ставкою 46,41%. Ставка 46,41% є ефективною ставкою по відношенню до ставки 40%, яка є номінальною, і обидві ставки ─ річні. Іноді ефективну ставку називають дійсною. Можемо дати інший варіант визначення ефективної ставки.

Ефективна ставка (дійсна ставка) дає відносний розмір доходу, який одержуємо в цілому за рік при річному нарахуванні процентів.

Позначимо ефективну ставку (наприклад, процентну) так: 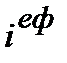або 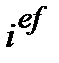(від англ. effective rate).

Повертаючись до визначення ефективної ставки бачимо, що є два варіанти «…при інших періодах нарахування процентів, відмінних від річного нарахування процентів».

Перший варіант. Нарахування процентів декілька разів на (за) рік:

─ два рази на рік, або по півріччям;

─ чотири рази на рік, або щоквартальне;

─ дванадцять разів на рік, або щомісячне;

─ 365 разів на рік, або щоденне;

─ інша кількість періодів нарахування, які менше року.

Застосовуємо, як це вже використовувалось раніше (див. формули 6.1, 6.2), позначки m ─ кількість нарахувань впродовж року та N ─ кількість років фінансової операції. Тоді, при піврічному нарахуванні процентів m=2, при щоквартальному нарахуванні процентів m=4, при щомісячному нарахуванні процентів m=12 і надалі ─ подібне чисельне визначення m.

Другий варіант. Період нарахування процентів довше за рік. Іншими словами, нарахування процентів менше одного разу на (за) рік:

─ один раз за два роки, m=1/2;

─ один раз за три роки, m=1/3;

─ один раз за півтора роки, m=1/1,5 = 0,6(6);

Використовуючи показники m та N при записі основних чотирьох формул (2.2), (2.10), (4.1), (4.5) (див. початок розділу 6) одержуємо їх модифікації в яких ставки проценту є номінальними за визначенням,─це формули (9.1), (6.2), (9.2), (6.4):

1) ─ формула простого нарахування процентів з використанням процентної ставки (основна формула 2.2):

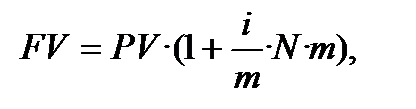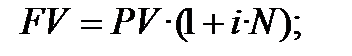або (9.1)

2) ─ формула складного нарахування процентів з використанням процентної ставки (основна формула 2.10):

(6.2)

3) ─ формула простого дисконтування з використанням облікової ставки (основна формула 4.1):

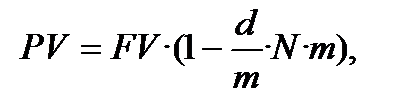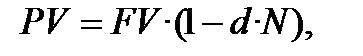або (9.2)

4) ─ формула складного дисконтування з використанням облікової ставки (основна формула 4.5):

(6.4)

Характеризуючи формули (9.1) та (9.2) треба зазначити, що використання номінальних ставок з введенням показника m та N не змінює характеристик цих формул, як не змінює і самих формул. Показник m у формулах (9.1) та (9.2) не застосовується, якщо у ці формули строк «підставляти» в роках (N ─ кількість років).

Щодо показника m у формулах складного нарахування процентів (6.2), (6.4), то формули «правильно спрацьовують» як при m > 1 (перший варіант ─ нарахування процентів декілька разів за рік), так і при m < 1 (другий варіант ─ період нарахування процентів довше за рік). При складному нарахуванні процентів для варіантів m > 1 та m < 1 формули одні і ті ж ─ (6.2), (6.4).

З іншої сторони, використовуючи показники ефективних ставок ( 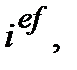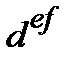) та показник N при записі основних чотирьох формул (2.2), (2.10), (4.1), (4.5) (див. початок розділу 6) одержуємо їх модифікації в яких ставки проценту є ефективними за визначенням─це формули (9.3), (9.4), (9.5), (9.6):

1) ─ формула простого нарахування процентів з використанням процентної ставки (основна формула 2.2):

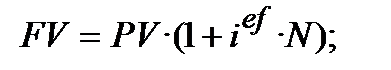(9.3)

2) ─ формула складного нарахування процентів з використанням процентної ставки (основна формула 2.10):

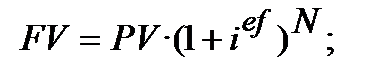(9.4)

3) ─ формула простого дисконтування з використанням облікової ставки (основна формула 4.1):

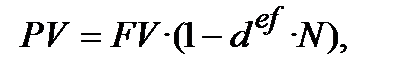(9.5)

4) ─ формула складного дисконтування з використанням облікової ставки (основна формула 4.5):

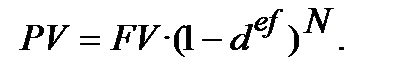(9.6)

При використанні номінальної ставки з m-разовим нарахуванням процентів за рік фактичний результат фінансової операції більший від річного нарахування процентів за тією ж номінальною ставкою.

Розрахунок ефективної ставки ставить за мету визначення такої 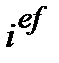або 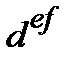, щоб за її використання отримувати такий самий фінансовий результат, як і за m-разового нарахування процентів за рік за ставкою i / m.

Отримання одного і того ж фінансового результату (FV=const), (PV=const), при одному і тому ж N, можливо за умови рівності множників нарощення для різних ставок процента і з отриманої рівності находження потрібного показника. Для одержання формул розрахунку ефективної ставки запишемо чотири множника формул (9.3), (9.4), (9.5), (9.6) і чотири множника формул (9.1), (6.2), (9.2), (6.4) у вигляді так званих квадратів ставок ефективності, рис. 9.1. На рисунку 9.1 всі множники записані, виходячи з вигляду всіх формул FV = PV·k, де k ─ множник нарощення або дисконтування.

Квадрат множників ефективних ставок

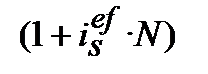
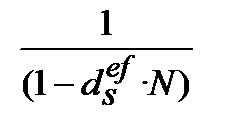
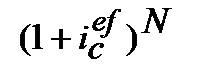
Квадрат множників номінальних ставок

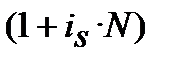
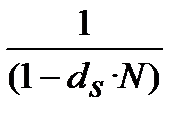
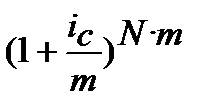
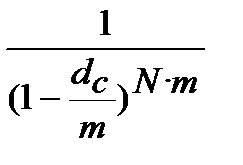
Рисунок 9.1 – Квадрати ставок ефективності: (де «і» ─ процентна ставка, «d» ─ облікова ставка, нижній індекс «s» означає, що ставки «і» та «d» прості (від англ. simpl), індекс «с» означає, що ставки «і» та «d» складні (від англ. compound), верхній індекс «ef» показує, що ставка ефективна (від англ.effective rate)).

Квадрати ставок ефективності дають можливість самостійно за допомогою звичайних алгебраїчних перетворень виводити формули розрахунку ефективних ставок. «Працюють» квадрати ставок ефективності таким чином. Треба взяти один з множників, що надано в квадраті множників ефективних ставок і дорівняти окремим рівнянням до кожного множника, що представлені у квадраті множників номінальних ставок. Потім, кожне рівняння розв’язати відносно ставки ефективності. Очевидно, що таких формул розрахунку ефективних ставок по співвідношенню до номінальних має бути шістнадцять.

1. Ефективну просту процентну ставку і 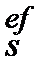, що відповідає номінальній простій процентній ставці 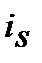знаходимо з дорівнювання множників

=

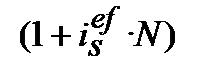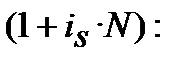
і 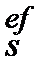= 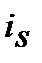(9.7)

2. Ефективну просту процентну ставку 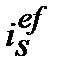що відповідає номінальній складній процентній ставці 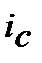знаходимо з дорівнювання множників

= :

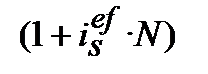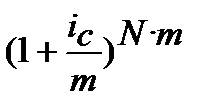(9.8)

3. Ефективну просту процентну ставку 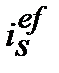, що відповідає номінальній простій обліковій ставці 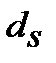знаходимо з дорівнювання множників

= :

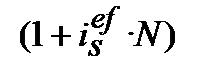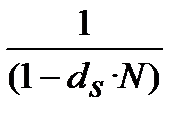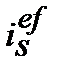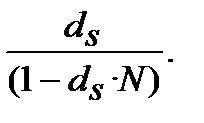= (9.9)

4. Ефективну просту процентну ставку 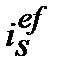що відповідає номінальній складній обліковій ставці знаходимо з дорівнювання множників

= :

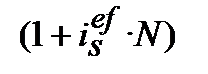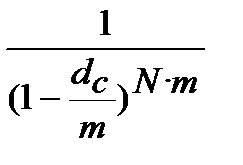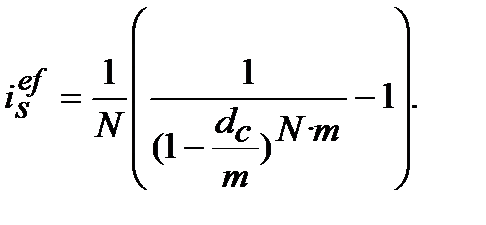(9.10)

5. Ефективну складну процентну ставку і 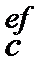, що відповідає номінальній простій процентній ставці 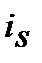знаходимо з дорівнювання множників

=

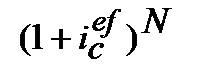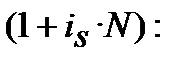
(9.11)

6. Ефективну складну процентну ставку і 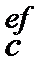, що відповідає номінальній складній процентній ставці знаходимо з дорівнювання множників

= :

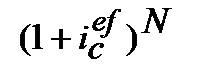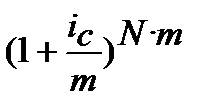(9.12)

7. Ефективну складну процентну ставку і 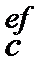, що відповідає номінальній простій обліковій ставці 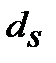знаходимо з дорівнювання множників

= :

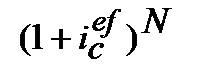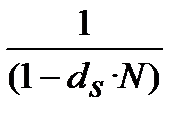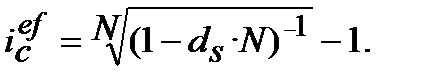(9.13)

8. Ефективну складну процентну ставку і 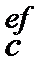, що відповідає номінальній складній обліковій ставці 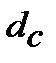знаходимо з дорівнювання множників

= :

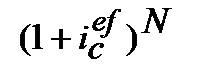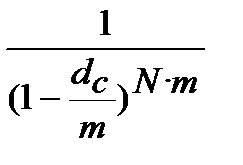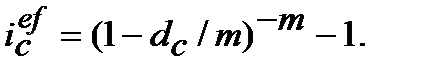(9.14)

9. Ефективну просту облікову ставку 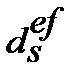, що відповідає номінальній простій процентній ставці 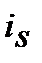знаходимо з дорівнювання множників

= :

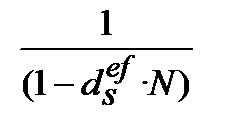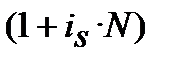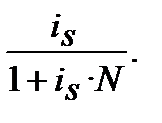= (9.15)

10. Ефективну просту облікову ставку 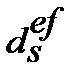, що відповідає номінальній складній процентній ставці 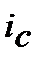знаходимо з дорівнювання множників

= :

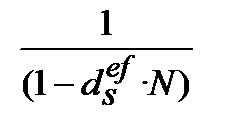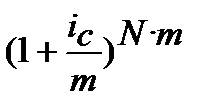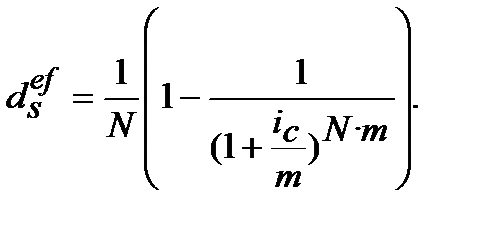(9.16)

11. Ефективну просту облікову ставку 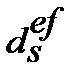, що відповідає номінальній простій обліковій ставці 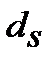знаходимо з дорівнювання множників

= :

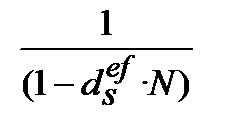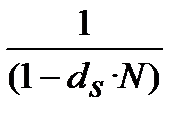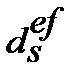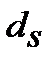= (9.17)

12. Ефективну просту облікову ставку 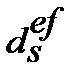, що відповідає номінальній складній обліковій ставці 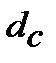знаходимо з дорівнювання множників

= :

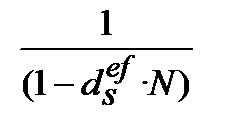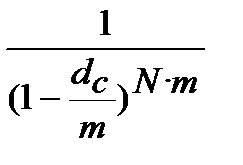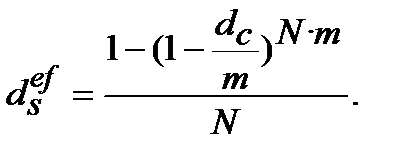(9.18)

13. Ефективну складну облікову ставку 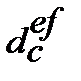, що відповідає номінальній простій процентній ставці знаходимо з дорівнювання множників

= :

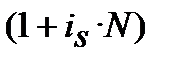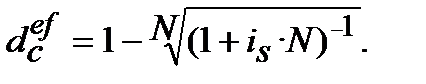(9.19)

14. Ефективну складну облікову ставку 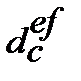, що відповідає номінальній складній процентній ставці 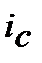знаходимо з дорівнювання множників

= :

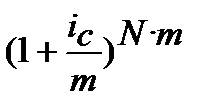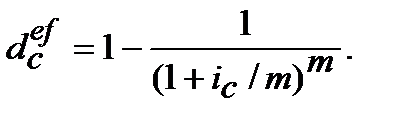(9.20)

15. Ефективну складну облікову ставку 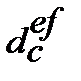, що відповідає номінальній простій обліковій ставці 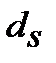знаходимо з дорівнювання множників

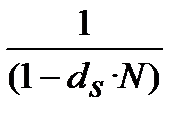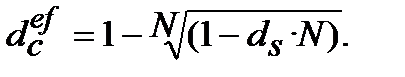= : (9.21)

16. Ефективну складну облікову ставку 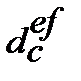, що відповідає номінальній складній обліковій ставці 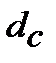знаходимо з дорівнювання множників

= :

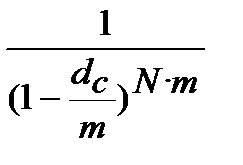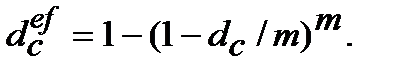(9.22)

Розуміння ролі показника ─ ефективна ставка, ─ досить важливе для фінансового аналізу. Справа в тому, що прийняття рішення про залучення коштів, наприклад банківської позики на тих або інших умовах, здійснюється частіше за все, виходячи з прийнятності ставки, що пропонується, яка в цьому випадку характеризує витрати позичальника. В рекламних оголошеннях ненавмисно або навмисно увагу на типі ставки зазвичай не акцентують, хоча в переважній кількості випадків мова йде про номінальну ставку, яка може вельми суттєво відрізнятися від ефективної ставки.

У фінансових операціях на практиці не має значення, яку зі ставок вказати ─ ефективну чи номінальну, якщо вони еквівалентні, тобто забезпечують одну і туж нарощену суму. В США в практичних розрахунках застосовують номінальну ставку (і, отже, використовують як основну, формулу (6.2): 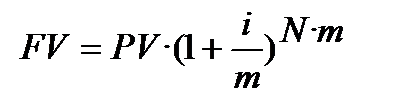). В європейських країнах , як правило, спочатку визначаються з ефективною ставкою і потім, як основну, використовують формулу (9.4):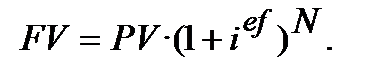

Результат розрахунку ефективних ставок може використовуватись як критерій ефективності, як критерій для порівнянь з метою вибору кращого варіанту. Можливе застосування ─ Приклад 9.2.

_Приклад 9.2___________________________________

Читайте також:

1. Розв’язування.
2. Розв’язування.
3. Розв’язування.
4. Розв’язування.
5. Розв’язування.
6. Розв’язування.
7. Розв’язування.
8. Розв’язування.
9. Розв’язування.
10. Розв’язування.
11. Системи та сукупності нерівностей з однією змінною та способи їх розв’язування. Нерівності та системи нерівностей з двома змінними, графічний спосіб їх розв’язування.

Переглядів: 960