• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Врахування впливу інфляції на результат фінансових операцій.

Як вже зазначалося, підрозділ 10.1 ─ це розрахунки, власне, показників інфляції. Підрозділ 10.2 ─ це застосування показників інфляції у фінансових розрахунках. А підрозділ 10.3 ─ це врахування впливу інфляції на результат фінансових операцій.

На поточний момент так склалося, що в практиці фінансових розрахунків та у сучасній фінансовій літературі врахування впливу інфляції на результат фінансових операцій переважно розглядається через перетворювальні операції з показниками інфляції у їх зв’язку зі ставками проценту. Всі такі перетворення ставлять за мету розрахунок таких узагальнюючих, таких інтегруючих ставок проценту, які враховують інфляційні процеси. По суті, всі такі перетворення є розрахунком еквівалентних ставок, які враховують інфляційні показники.

Розглянемо різні випадки розрахунку еквівалентних ставок нарахування процентів з врахуванням інфляції.

Для механізму простого нарахування процентів згідно формули (2.2) одержуємо:

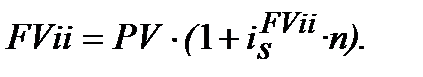
В той же час необхідно виконати рівняння:

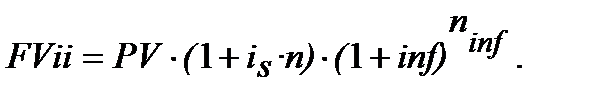(10.16)

Складаємо рівняння еквівалентності:

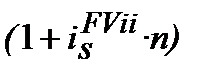
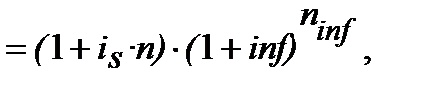
з якого одержуємо:

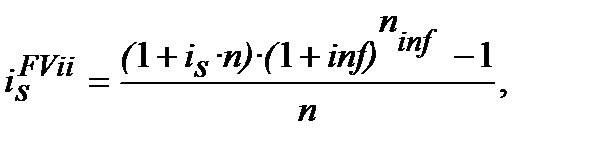(10.23)

де 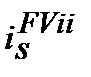─ проста (simpl)процентна еквівалентна ставка (еквівалентна простій 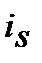та inf) для розрахунку майбутньої вартості з урахуванням компенсації (ii ─ inflationery increase) інфляційного зростання (inf) цін.

Ставка 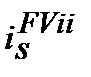є скоригованою на рівень інфляції. Корегування відбувається шляхом збільшення майбутньої суми таким чином, що інфляційне знецінення повністю компенсується додатковою сумою грошей і тому ставка 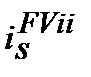за розміром є завжди більшою за 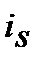. Таку скориговану на інфляцію ставку у фінансовій літературі зарубіжжя досить часто називають брутто-ставкою. Брутто-ставка ─ це термін, який запозичено з теорії страхових (актуарних) розрахунків. За аналогією номінальну ставку 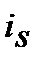можуть називати нетто-ставкою. Четыркин в [15, стор. 87] звертає увагу, що в фінансовій літературі зарубіжжя брутто-ставку іноді називають номінальною. В наших розрахунках цей термін уже «зайнятий».

Продовжимо розгляд розрахунків еквівалентних ставок нарахування процентів з врахуванням інфляції. Рівняння еквівалентності від формули (10.18):

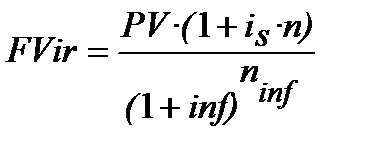(10.18)

має вигляд:

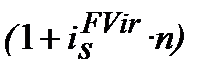
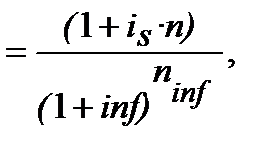
з якого одержуємо:

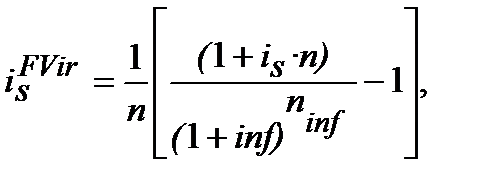(10.24)

де 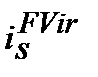─ проста (simpl)процентна еквівалентна ставка (еквівалентна простій 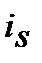та inf) для розрахунку майбутньої вартості з врахуванням її (майбутньої вартості) інфляційного знецінення (inflationery reality).

Ставка 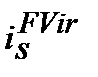має назву ─ реальна ставка. Ставку 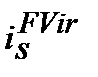можуть також назвати або ставкою доходності або ставкою реальної доходності. Реальна ставка показує зростання (або зменшення) майбутньої вартості без додаткової грошової компенсації на покриття інфляційних втрат. Якщо зростання є, то воно відбувається за рахунок номінальної ставки, тобто реальна ставка показує, що нарощення, спричинене номінальною ставкою, більше за втрати від інфляції.

Для простих облікових ставок аналогічні еквівалентні рівняння будуть мати вигляд:

─ від формул (4.1) та (10.21)

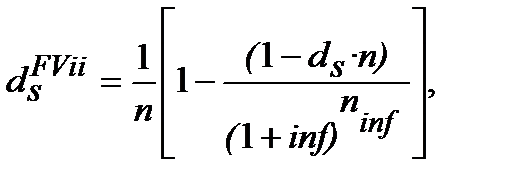(10.25)

де 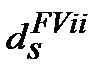─ проста (simpl)облікова еквівалентна ставка (еквівалентна простій 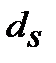та inf) для розрахунку майбутньої вартості з урахуванням компенсації (ii ─ inflationery increase) інфляційного зростання (inf) цін, 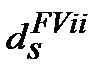може мати назву ─ облікова проста брутто-ставка;

─ від формул (4.1) та (10.22)

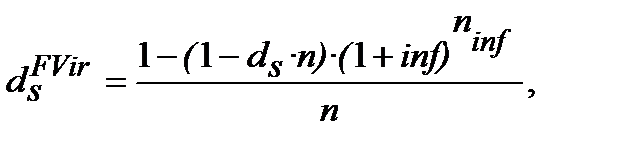(10.26)

де 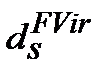─ проста (simpl)облікова еквівалентна ставка (еквівалентна простій 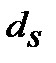та inf) для розрахунку майбутньої вартості з врахуванням її (майбутньої вартості) інфляційного знецінення (inflationery reality), 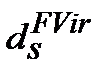може називатися реальною обліковою простою ставкою або обліковою простою ставкою реальної доходності.

Для механізму складного нарахування процентів на підставі формули (2.10) одержуємо:

З іншої сторони необхідно додержуватись рівняння:

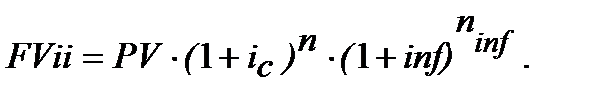(10.14)

Складаємо рівняння еквівалентності:

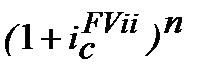
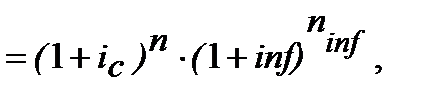
з якого одержуємо:

(10.27)

де 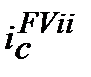─ складна ( від ─ compound)процентна еквівалентна ставка (еквівалентна складній 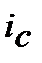та inf) для розрахунку майбутньої вартості з урахуванням компенсації (ii ─ inflationery increase) інфляційного зростання (inf) цін. Іншими словами 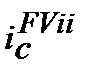─ це складна процентна брутто-ставка.

Рівняння еквівалентності від формули (10.17):

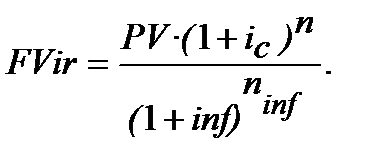(10.17)

має вигляд:

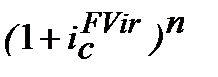
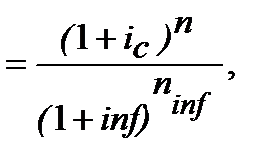
з якого одержуємо:

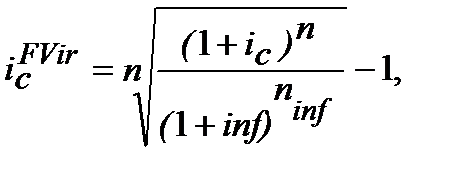(10.28)

де ─ складна ( від ─ compound) процентна еквівалентна ставка (еквівалентна складній та inf) для розрахунку майбутньої вартості з врахуванням її (майбутньої вартості) інфляційного знецінення (inflationery reality). Або, що одне і те ж, 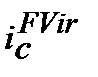─ складна реальна процентна ставка або процентна ставка реальної доходності при складному нарахуванні процентів.

Якщо нарахування процентів декілька разів на рік (m), використовуємо формулу (6.2) і маємо рівняння еквівалентності:

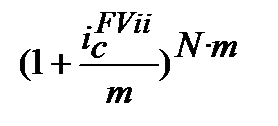
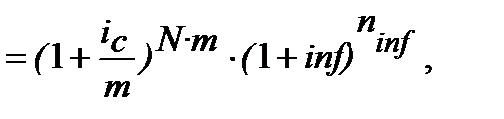
з якого:

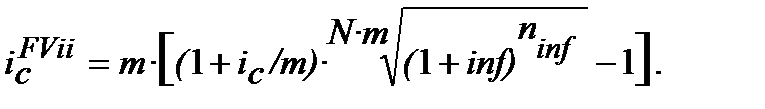(10.29)

Від рівняння еквівалентності:

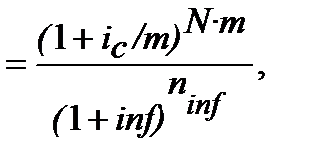
маємо таку формулу:

(10.30)

Таким же чином одержуємо формули у випадку застосування складних облікових ставок.

Для складних облікових ставок аналогічні еквівалентні рівняння будуть мати вигляд:

─ від формул (4.5) та (10.19):

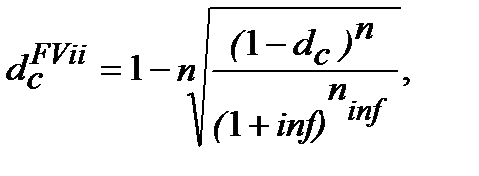(10.31)

де 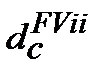─ складна (compound)облікова еквівалентна ставка (еквівалентна складній 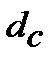та inf) для розрахунку майбутньої вартості з урахуванням компенсації (ii ─ inflationery increase) інфляційного зростання (inf) цін;

─ від формул (4.5) та (10.20):

(10.32)

де 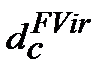─ складна (compound)облікова еквівалентна ставка (еквівалентна простій 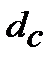та inf) для розрахунку майбутньої вартості з врахуванням її (майбутньої вартості) інфляційного знецінення (inflationery reality).

Якщо нарахування процентів декілька разів на рік (m), використовуємо формулу (6.4) і маємо формули еквівалентності:

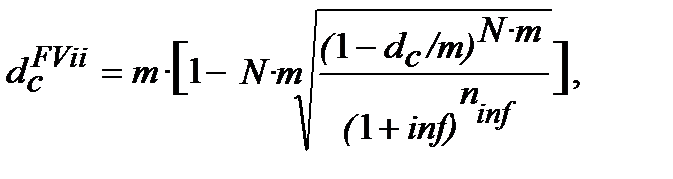(10.33)

(10.34)

В практиці фінансових обчислень досить часто використовують показники для проведення швидкого приблизного аналізу. Вираховують таки показники за певних умов. За неоголошеними правилами за умови розрахунку багатьох аналітичних показників беруть за основу річні показники. Наприклад, наведений нижче аналіз реальної ставки є випадком, коли = 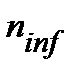і обидва вони ( 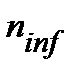) дорівнюють одиниці, тобто, нарахування процентів ─ річне та рівень інфляції ─ також річний. За таких умов ставка реальної доходності при складному нарахуванні процентів, формула (10.28), перетворюється в просту формулу:

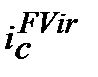
(10.35)

Доречи, формула простої ставки реальної доходності (10.24) за річних показників також стає формулою (10.35). Формула (10.35) допомагає показати декілька моментів з аналізу реальної доходності:

─ якщо 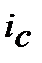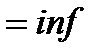(доходність вкладень дорівнює темпу інфляції), то 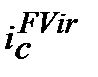= 0, тобто весь дохід поглинається інфляцією;

─ якщо 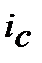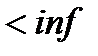(доходність вкладень нижче рівня інфляції), то 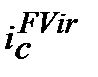< 0, тобто фінансова операція збиткова;

─ якщо 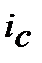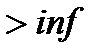(доходність вкладень вище рівня інфляції), то 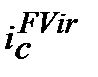> 0, тобто фінансова операція має реальний приріст вкладеного капіталу.

Нагадуємо, що всі ці висновки справедливі при умовах: строк операції ─ рік, нарахування процентів ─ річне, рівень інфляції ─ показник за рік.

В завершення підрозділу 10.3 можемо констатувати, що при врахуванні інфляції відрізняють наступні види ставок процента. Номінальна ставка (процентна і облікова) ─ це початкова ставка, що вказана в договорах (її можна вважати за базову і, як правило, вона річна, номінальна). Доходність, розрахована за цією ставкою, не скоригована на інфляцію. Реальна ставка показує доходність з врахуванням інфляції, яка характеризується падінням купівельної спроможності грошей. Реальна процентна ставка в умовах інфляції завжди менше номінальної і можна бути навіть від’ємною. Компенсаційна ставка або брутто-ставка ─ це ставка, за якої буде збільшення вартості капіталу на розмір номінальної ставки не зважаючи на наявність інфляції. Також, реальні ставки та брутто-ставки можуть нести назву ─ позитивна ставка. Позитивна ставка ─ це будь яка ставка, за якої буде збільшення вартості капіталу при наявності інфляції. Брутто-ставка ─ завжди позитивна, а реальна ─ не завжди.

_Приклад 10.2__________________________________

Читайте також:

1. I визначення впливу окремих факторів
2. I етап. Аналіз впливу типів ринку на цінову політику.
3. VIII. Реакції, в результаті яких утворюються високомолекулярні сполуки
4. XV. Фінансові результати від первісного визнання та реалізації сільськогосподарської продукції та додаткових біологічних активів
5. Абсолютні та відності показники результатів діяльності підприємства.
6. Адекватним фізичним критерієм оцінки її впливу на організм люди1
7. Аденогіпофіз, його гормони, механізм впливу
8. Аденогіпофіз, його гормони, механізм впливу, прояви гіпер- та гіпофункцій.
9. Акцентуація характеру – перебільшений розвиток певних властивостей характеру на шкоду іншим, в результаті чого погіршуються відносини з оточуючими людьми.
10. Амортизація як джерело фінансових ресурсів підприємств
11. Аналіз відхилень від нормативів та їх впливу на прибуток
12. Аналіз впливу постачальників

Переглядів: 857