
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Двоїстий СМ
Як було сказано вище, між вихідною і ДЗ існує відповідність. Виникає питання про існування зв’язку (відповідності) між їхніми розв’язками. Для цього розглянемо метод, який дозволяє отримати розв’язки вихідної і ДЗ. Його будемо називати двоїстим СМ. Розглянемо наступну ЗЛП: знайти найбільше значення функції
 (1.31)
(1.31)
при обмеженнях

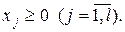 (1.32)
(1.32)
Тоді двоїстою до неї буде: знайти найменше значення функції
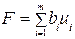 , (1.33)
, (1.33)
при обмеженнях
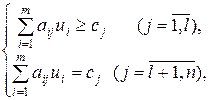 (1.34)
(1.34)

Вихідні дані пари ДЗ можна представити в одній симплексній таблиці, перетворивши самі задачі. Введемо для вихідної задачі змінні 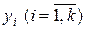 так, щоб вона звелася до задачі в канонічній формі. Тоді (1.32) набуде вигляду:
так, щоб вона звелася до задачі в канонічній формі. Тоді (1.32) набуде вигляду:

Далі,
 (1.35)
(1.35)
Змінні  будуть базисними. Для ДЗ введемо змінні
будуть базисними. Для ДЗ введемо змінні  так, щоб
так, щоб
 (1.36)
(1.36)
Враховуючи вищесказане, прийдемо до наступної таблиці 1.4
Таблиця 1.4
| v1 | v2 | … | vl | … | F | ||||
| –x1 | –x2 | … | –xl | –xl+1 | … | –xn | |||
| u1 | y1 | a11 | a12 | … | a1l | a1,l+1 | … | a1n | b1 |
| u2 | y2 | a21 | a22 | … | a2l | a2,l+1 | … | a2n | b2 |
| … | … | … | … | … | … | … | … | … | … |
| uk | yk | ak1 | ak2 | … | akl | ak,l+1 | … | akn | bk |
| uk+1 | ak+1,1 | ak+1,2 | … | ak+1,l | ak+1,l+1 | … | ak+!,n | bk+1 | |
| … | … | … | … | … | … | … | … | … | … |
| um | am1 | am2 | … | aml | am,l+1 | … | amn | bm | |
| f | –c1 | –c2 | … | –cl | –cl+1 | … | –cn |
Відомо, що якщо вихідна задача має розв’язок, то його має і двоїста, причому  . Розв’язуючи вихідну задачу і маючи відповідність між змінними вихідної і ДЗ:
. Розв’язуючи вихідну задачу і маючи відповідність між змінними вихідної і ДЗ: 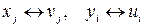 , ми можемо записати її оптимальний розв’язок.Розглянемо конкретний приклад реалізації двоїстого СМ.
, ми можемо записати її оптимальний розв’язок.Розглянемо конкретний приклад реалізації двоїстого СМ.
Приклад 1.7. Записати ДЗ до задачі: знайти найбільше значення функції 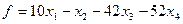 при обмеженнях
при обмеженнях
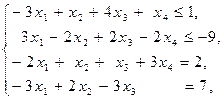

і знайти її розв’язок двоїстим СМ.
Розв’язок. Використовуючи алгоритм запису пари ДЗ, одержимо наступну ДЗ: знайти найменше значення функції  при обмеженнях:
при обмеженнях:

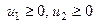 , u3, u4 – вільні змінні.
, u3, u4 – вільні змінні.
Вихідні дані пари ДЗ помістимо в симплексну таблицю:
| v1 | v2 | v3 | v4 | F | |||
| –x1 | –x2 | –x3 | –x4 | ||||
| u1 | y1 | –3 |  1 1
| 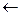
| |||
| u2 | y2 | –2 | –2 | –9 | |||
| u3 | –2 | ||||||
| u4 | –3 | –3 | |||||
| f | –10 | ||||||

|
Розв’язуючи вихідну задачу, виключаємо 0–рядки, а заодно і вільні змінні для двоїстої. В першому 0-рядку вибираємо будь-який додатний коефіцієнт, наприклад, (1) з другого стовпчика і складаємо відношення

На перетині першого рядка і другого стовпчика лежить розв’язуючий елемент (1). Здійснивши один крок перетворень Жордана-Гаусса, прийдемо до наступної таблиці
| v1 | u1 | v3 | v4 | F | |||
| –x1 | –y1 | –x3 | –x4 | ||||
| v2 | x2 | –3 | |||||
| u2 | y2 | –3 | –7 | ||||
| u3 |  1 1
| –1 | –3 | 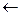
| |||
| u4 | –2 | –11 | –2 | ||||
| f | –7 | –1 | –1 | ||||

|
Оскільки 0-рядки не виключені, то в першому 0-рядку вибираємо додатний елемент (1) і складаємо відношення вільних членів до однойменних за знаком елементів розв’язуючого стовпчика:

Число (1), яке є розв’язуючим елементом, належить до розглядуваного 0-рядка. Після здійснення одного кроку перетворень Жордана-Гаусса , отримаємо
| u3 | u1 | v3 | v4 | F | ||
| –y1 | –x3 | –x4 | ||||
| v2 | x2 | –2 | –5 | |||
| u2 | y2 | –1 | –4 | |||
| v1 | x1 | –1 | –3 | |||
| u4 | –3 | –2 | –8 | |||
| f | –8 |
Виписуємо співвідношення для визначення вільної змінної u3, а даний стовпчик виключаємо з таблиці:  ,
,
| u1 | v3 | v4 | F | |||
| –y1 | –x3 | –x4 | ||||
| v2 | x2 | –2 | –5 | |||
| u2 | y2 | –1 | –4 | |||
| v1 | x1 |  –1 –1
| –3 | |||
| u4 | –2 | –8 | 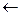
| |||
| f | –8 | |||||

|
Оскільки існує єдине відношення  , то елемент (1) 0–рядка буде розв’язуючим. Здійснивши один крок перетворень Жордана-Гаусса, отримаємо
, то елемент (1) 0–рядка буде розв’язуючим. Здійснивши один крок перетворень Жордана-Гаусса, отримаємо
| u4 | v3 | v4 | F | ||
| –x3 | –x4 | ||||
| v2 | x2 | –9 | –9 | ||
| u2 | y2 | –1 | –2 | –2 | |
| v1 | x1 | –5 | –6 | ||
| u1 | y1 | –2 | –8 | ||
| f |
Звідси  . Викресливши 0-стовпчик і провівши послідовно один за одним два перетворення Жордана-Гаусса, прийдемо до наступних симплексних таблиць
. Викресливши 0-стовпчик і провівши послідовно один за одним два перетворення Жордана-Гаусса, прийдемо до наступних симплексних таблиць
| v3 | v4 | F | u2 | v4 | F | ||||||
| –x3 | –x4 | –y2 | –x4 | ||||||||
| v2 | x2 | –9 | –9 | v2 | x2 | –9 |  9 9
| ||||
| u2 | y2 | –1 | –2 | –2 | 
| v3 | x3 | –1 | 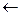
| ||
| v1 | x1 | –5 | –6 | v1 | x1 | –5 | |||||
| u1 | y1 | –2 | –8 | u1 | y1 | –2 | –4 | ||||
| f | f | –1 | |||||||||

| 
|
| u2 | v3 | F | ||
| –y2 | –x3 | |||
| v2 | x2 | |||
| v4 | x4 | |||
| v1 | x1 | |||
| u1 | y1 | |||
| f | 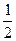
| 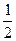
|
З останньої таблиці виписуємо оптимальний розв’язок вихідної задачі: 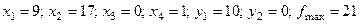 і двоїстої
і двоїстої 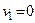 ;
; 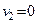 ;
; 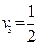 ;
;  ;
;  ;
;  ;
; 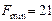 .
.
Значення вільних змінних u3, u4 ДЗ будуть:
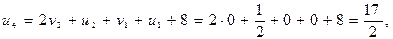
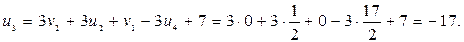
Контрольні запитання та задачі
1. Складіть математичну модель задачі розподілу ресурсів, запишіть до неї ДЗ і дайте їх економічну інтерпретацію.
2. Сформулюйте алгоритм запису ДЗ.
3. Який зв’язок між розв’язками вихідної та ДЗ і який метод дозволяє їх знаходити?
4. Який вигляд має симплексна таблиця для пари ДЗ?
5. Сформулюйте основну нерівність двоїстості.
6. В якому випадку допустимі плани пари ДЗ будуть оптимальними?
7. Яка необхідна і достатня умова того, щоб задачі двоїстої пари мали оптимальні плани?
8. Яка необхідна і достатня умова того, щоб допустимі плани пари ДЗ були оптимальними?
9. Чому дорівнює оптимальна оцінка ресурсу, який використовується не повністю?
10. Яка оцінка відповідає найбільш дефіцитному ресурсу?
11. На що вказує величина двоїстої оцінки певного ресурсу?
12. Побудувати ДЗ до ЗЛП, в якій потрібно знайти найбільше значення функції  .
.
а)

| б)

| в)
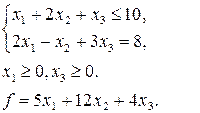
|
г)

| д)
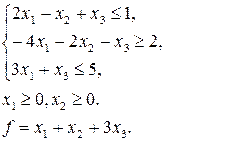
| е)
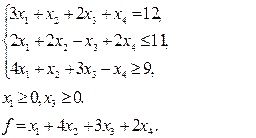
|
є)

| ж)
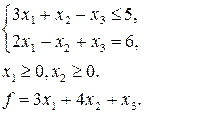
| з)
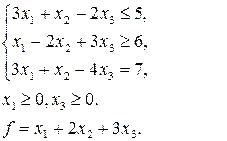
|
и)

|
Читайте також:
| <== попередня сторінка | | | наступна сторінка ==> |
| Загальні зауваження | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |