
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Загальні зауваження
Кожній ЗЛП можна поставити у відповідність деяку іншу задачу, яку будемо називати двоїстою (ДЗ) по відношенню до першої. Тобто в ЛП можна говорити про існування пари ДЗ. Першу задачу ми будемо називати вихідною, а другу – двоїстою до першої і навпаки. Цільова функція і обмеження ДЗ цілком визначаються умовами вихідної задачі. Виявляється, що якщо знайти розв’язки однієї із задач пари ДЗ, то цим цілком визначаються розв’язки іншої.
Розглянемо методику побудови ДЗ до задачі розподілу ресурсів. Як відомо, математична модель такої задачі має вигляд: знайти найбільше значення функції
 (1.27)
(1.27)
при обмеженнях
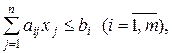
 (1.28)
(1.28)
Задачу (1.27) – (1.28) будемо вважати вихідною. Складемо двоїсту до неї. Для цього введемо змінні  (їх кількість дорівнює кількості обмежень m вихідної задачі), які будемо називати уявними цінами. Зміст цього терміну стане зрозумілим пізніше.
(їх кількість дорівнює кількості обмежень m вихідної задачі), які будемо називати уявними цінами. Зміст цього терміну стане зрозумілим пізніше.
Нехай  – цільова функція. Якщо
– цільова функція. Якщо 
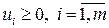 – ціна одиниці сировини, то F визначатиме витрати на сировину. Тоді ДЗ запишеться так: знайти найменше значення функції
– ціна одиниці сировини, то F визначатиме витрати на сировину. Тоді ДЗ запишеться так: знайти найменше значення функції
 (1.29)
(1.29)
при обмеженнях (витрати на одиницю виробу повинні бути не менші за його ціну)
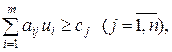
 (1.30)
(1.30)
Задачі (1.27) – (1.30) утворюють пару ДЗ.
Сформулюємо алгоритм побудови пари ДЗ:
1. Вводимо змінні ДЗ. Їх кількість дорівнює кількості обмежень (не рахуючи обмежень невід’ємності змінних) вихідної задачі.
2. Коефіцієнтами цільової функції ДЗ є вільні члени вихідної задачі.
3. Коефіцієнтами матриці обмежень ДЗ є коефіцієнти транспонованої матриці системи обмежень вихідної задачі.
4. Вільними членами системи обмежень ДЗ є коефіцієнти цільової функції для вихідної задачі.
5. Якщо цільова функція вихідної задачі максимізується, то ДЗ – мінімізується, причому  .
.
Дамо економічну інтерпретацію вихідної та ДЗ.
Економічна інтерпретація задачі (1.27)–(1.28): скільки і якої продукції потрібно виготовити для того, щоб при заданих ресурсах  цінах
цінах 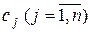 і питомих затратах
і питомих затратах  максимізувати прибуток f від реалізації виготовленої продукції.
максимізувати прибуток f від реалізації виготовленої продукції.
Економічна інтерпретація задачі (1.29)–(1.30): якою повинна бути ціна одиниці сировини  для того, щоб при заданих ресурсах
для того, щоб при заданих ресурсах 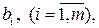 цінах за одиницю продукції
цінах за одиницю продукції  , питомих затратах
, питомих затратах  мінімізувати витрати на сировину.
мінімізувати витрати на сировину.
Приклад 1.5. Скласти ДЗ до задачі: знайти найбільше значення функції  при обмеженнях
при обмеженнях
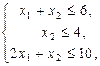
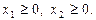
Розв’язок. Введемо змінні ДЗ  (кількість рівна кількості обмежень вихідної задачі). Тоді ДЗ запишеться: знайти найменше значення функції
(кількість рівна кількості обмежень вихідної задачі). Тоді ДЗ запишеться: знайти найменше значення функції  при обмеженнях
при обмеженнях
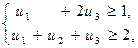
 .
.
Якщо вихідна задача представлена в загальному виді, то до пунктів (1) – (5) алгоритму запису ДЗ слід додати наступні.
6. Обмеженням типу рівності в вихідній задачі будуть відповідати вільні змінні ДЗ і навпаки (вільним змінним вихідної задачі відповідають обмеження типу рівності ДЗ).
7. В обмеженнях типу рівності в вихідній задачі вільний член повинен бути невід’ємним. Якщо він від’ємний, то відповідне обмеження в вихідній задачі слід помножити на (–1).
8. Обмеженням типу нерівності вихідної задачі відповідають невід’ємні змінні ДЗ.
9. Якщо вихідна задача містить обмеження  , то обмеження в ДЗ будуть протилежними, тобто
, то обмеження в ДЗ будуть протилежними, тобто  , причому якщо у вихідній задачі функція максимізується, то обмеження мають бути
, причому якщо у вихідній задачі функція максимізується, то обмеження мають бути  , якщо мінімізується, то
, якщо мінімізується, то  .
.
Таким чином, для запису ДЗ слід спочатку систему обмежень вихідної задачі звести до обмежень з однаковим знаком  або
або  , а потім скористатися вищенаведеним алгоритмом запису пари ДЗ (п.п.1–9).
, а потім скористатися вищенаведеним алгоритмом запису пари ДЗ (п.п.1–9).
Приклад 1.6. Записати ДЗ до задачі: знайти найбільше значення функції
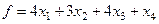 при обмеженнях
при обмеженнях
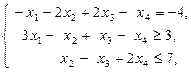
 х4 – вільна змінна.
х4 – вільна змінна.
Розв’язок. Перше і друге обмеження помножимо на (–1). Одержимо:

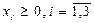
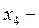 вільна змінна.
вільна змінна.
ДЗ матиме вигляд: знайти найменше значення функції  при обмеженнях
при обмеженнях
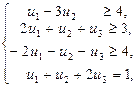
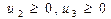 , и1 – вільна змінна.
, и1 – вільна змінна.
1.5.2. Теореми двоїстості. Економічний зміст оптимальних планів пари ДЗ
Теореми двоїстості (подаємо без доведень) вказують на взаємозв’язок між допустимими та оптимальними планами, цільовими функціями та системами обмежень пари ДЗ (1.27)–(1.28) і (1.29)–(1.30).
Сформулюємо спочатку основну нерівність двоїстості: для будь-яких допустимих планів  ,
,  прямої і двоїстої задач завжди справедлива нерівність
прямої і двоїстої задач завжди справедлива нерівність  або
або 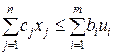 .
.
Теорема 1.7. Якщо 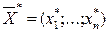 і
і  – допустимі плани пари ДЗ (1.27)–(1.28) і (1.29)–(1.30), для яких виконується рівність
– допустимі плани пари ДЗ (1.27)–(1.28) і (1.29)–(1.30), для яких виконується рівність  , то
, то 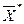 – оптимальний план задачі (1.27)–(1.28), а
– оптимальний план задачі (1.27)–(1.28), а 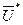 – задачі (1.29)–(1.30).
– задачі (1.29)–(1.30).
Теорема1.8. Для того, щоб задачі двоїстої пари мали оптимальні плани, необхідно і досить, щоб кожна з цих задач мала хоча б один допустимий план.
Теорема1.9. Якщо одна з ДЗ має оптимальний план, то і інша теж має оптимальний план, причому для будь-яких оптимальних планів 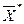 і
і 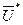 виконується рівність
виконується рівність  .
.
Якщо ж одна з ДЗ нерозв’язна (  або
або 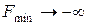 ), то друга задача не має допустимих планів. Якщо одна з пари взаємно ДЗ не має допустимого плану, то звідси не випливає, що цільова функція другої задачі необмежена.
), то друга задача не має допустимих планів. Якщо одна з пари взаємно ДЗ не має допустимого плану, то звідси не випливає, що цільова функція другої задачі необмежена.
Для задачі розподілу ресурсів (1.27) – (1.28) теорема 1.3 означає, що максимально можливий прибуток 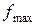 від реалізації продукції співпадає з мінімально можливою вартістю сировини
від реалізації продукції співпадає з мінімально можливою вартістю сировини  .
.
Теорема1.10. Для оптимальності допустимих планів 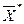 і
і 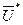 прямої і двоїстої задач (1.27)–(1.28) і (1.29)–(1.30) необхідно і достатньо, щоб виконувались співвідношення: якщо
прямої і двоїстої задач (1.27)–(1.28) і (1.29)–(1.30) необхідно і достатньо, щоб виконувались співвідношення: якщо  , то
, то 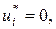 якщо
якщо 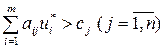 , то
, то 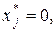 де
де  і
і 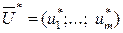 – оптимальні плани відповідно прямої і ДЗ.
– оптимальні плани відповідно прямої і ДЗ.
З економічної точки зору розв’язування вихідної задачі дозволяє отримати оптимальний план випуску продукції, а розв’язування двоїстої – оптимальну систему умовних оцінок використаних ресурсів.
Оптимальні плани пари взаємно ДЗ зв’язані не тільки рівністю значень цільових функцій, але й іншими співвідношеннями. Так на основі теореми 1.10 встановлюється зв’язок між обмеженнями і змінними пари взаємно ДЗ. Розглядатимемо вихідну задачу як задачу про розподіл ресурсів, а двоїсту – про визначення умовних оцінок ресурсів. Тоді змінні і обмеження будуть зв’язані наступним чином: якщо за оптимальним планом вихідної задачі деякий і-ий ресурс використовується не повністю, тобто 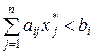 , то його оптимальна оцінка дорівнює нулю (
, то його оптимальна оцінка дорівнює нулю (  ); якщо ж затрати на ресурси, які використовуються при виробництві одиниці j-го продукту, перевищують дохід від його реалізації, то він не виробляється, тобто
); якщо ж затрати на ресурси, які використовуються при виробництві одиниці j-го продукту, перевищують дохід від його реалізації, то він не виробляється, тобто  .
.
Таким чином, можемо стверджувати, що позитивну двоїсту оцінку можуть мати лише ресурси, які повністю використовуються в оптимальному плані; оцінки не повністю використаних ресурсів завжди рівні нулю. Найбільшій величині оцінки відповідає найбільш дефіцитний ресурс, недефіцитному ресурсу відповідає оцінка, рівна нулю. Величина двоїстої оцінки певного ресурсу показує, на скільки зросло б максимальне значення цільової функції, якщо б об’єм даного ресурсу збільшився на одиницю.
Читайте також:
- I. Загальні збори АТ
- I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
- II. ЗАГАЛЬНІ ПОЛОЖЕННЯ.
- А) загальні критерії
- Білковий обмін: загальні відомості
- Вальниці ковзання. Загальні відомості
- Вимір дохідності та загальні підходи до оцінки ефективності управління інвестиційним портфелем.
- ВИМОГИ ДО ОБ'ЄМНО-ПЛАНУВАЛЬНИХ РІШЕНЬ ГАРАЖІВ Загальні вимоги
- Власні і загальні іменники як лексико-граматичні розряди за специфікою виявлення категорії числа
- Встановлення заземлень. Загальні вимоги.
- Вступ. Загальні відомості про ідентифікацію.
- Вступ. Загальні питання охорони праці
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Двоїстий СМ |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |