• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

На оформлення замовлень

Розглянемо модель, у якій враховуються витрати на оформлення замовлення . Нехай M{C1(q)} – сумарні очікувані витрати у системі, включаючи витрати на оформлення замовлення. Тоді математичне сподівання цих витрат дорівнює

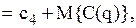(3.31)

де – функція витрат, визначена у попередній моделі (без врахування витрат на оформлення замовлення).

Як показано у моделі 1, мінімальне значення має місце при значенні 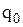, яке задовольняє умові

(3.32)

де 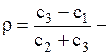щільність збитків.

Оскільки 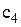є константою, то мінімальне значення також повинно мати місце при значенні 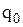. Криві і наведені на де введені нові позначення s і S, які використовуються у подальшому.

Значення S дорівнює 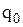, значення s (s < S) дорівнює нижньому рівню запасів і визначається із рівняння

. (3.33)

Тепер задачу можна сформулювати наступним чином: визначити кількість продукції q, яку слід замовляти, якщо перед розміщенням замовлення є z одиниць запасу і нижній рівень запасу дорівнює s.

Задача розв’язується при трьох умовах:

1) z < s;

2)

3) z > S.

Випадок 1: Оскільки у наявності вже є одиниць продукції, то витрати зберігання запасу складають . Якщо замовляти будь-яку додаткову кількість продукції 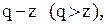то відповідні витрати при заданому q складуть , включаючи витрати на оформлення замовлення. Із випливає, що при будь-якому

(3.34)

Таким чином, оптимальний рівень запасу повинен досягати 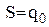і розмір замовлення повинен бути рівним .

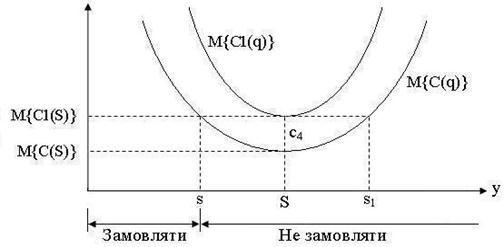
Рис. 3.6. Графіки функцій

Випадок 2: 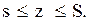Як і раніше, із рис. 3.6 випливає, що

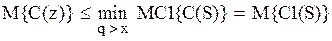. (3.35)

Тому у даному випадку при умові, що нове замовлення не подається, додаткових витрат не виникає. Отже,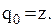

Випадок 3: z > S. Із рис. 3.5 випливає, що

. (3.36)

Це знову показує, що якщо замовлення не подається, то витрати тільки знизяться і

Ця стратегія, яка називається -стратегією, визначається правилом

якщо 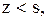замовляти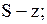

якщо 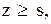замовляти не потрібно.

Оптимальність -стратегії випливає із того, що функція витрат вгнута. У загальному випадку, коли ця властивість не виконується, -стратегія перестає бути оптимальною.

Приклад 3.10. Щоденний попит на продукцію протягом одного періоду задовольняється миттєво на початку періоду. Попит є випадковою величиною, рівномірно розподіленою на інтервалі від 280 до 320 одиниць. Вартість одиниці продукції дорівнює 40 грн., вартість подачі замовлення 25 грн. Вартість зберігання одиниці продукції протягом періоду дорівнює 10 грн., а штраф за дефіцит одиниці продукції – 75 грн. Початковий запас дорівнює 10 одиницям. Визначимо оптимальну стратегію замовлення продукції – оптимальний обсяг замовлення 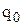і нижній рівень запасу .

Спочатку визначаємо оптимальній рівень запасу 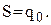Потім знаходимо величину s і визначаємо стратегію управління запасами.

Читайте також:

1. VI. Оформлення маршрутної документації на проведення туристичних походів та експедицій
2. Аналіз і оптимізація обсягів замовлень
3. Аналіз і оптимізація обсягів замовлень
4. Банк приймає до оплати вимога-доручення від платника протягом 20 календарних днів із дати оформлення його одержувачем.
5. Вантажна митна декларація як основний документ при здійсненні митного оформлення вантажів
6. Види бойових документів і вимоги до їх оформлення
7. Види бойових документів і вимоги до їх оформлення
8. ВИМОГИ ДЕРЖСТАНДАРТУ ДО ОФОРМЛЕННЯ ДОКУМЕНТІВ.
9. Вимоги до інтонаційного оформлення прочитуваного і декламованого. Прийоми його навчання
10. ВИМОГИ ДО ОФОРМЛЕННЯ АНКЕТИ
11. Вимоги до оформлення документів, які подаються державному реєстратору
12. Вимоги до оформлення документів, які подаються державному реєстратору.

Переглядів: 539