В потенціальній ямі

Мета: ознайомитись із особливостями енергетичного спектру мікрочастинок, що перебувають в потенціальній ямі та навчитись визначати за допомогою отриманих експериментальних даних фізичні сталі та характеристики елементарних частинок.

Устаткування: комп’ютерна програма “Частинка в потенціальній ямі”.

Теоретичні відомості

У квантовій фізиці частка, що рухається у вільному просторі, може мати будь-яку енергію. Її енергетичний спектр – суцільний. У частки, що рухається в силовому полі, що утримує її в обмеженій області простору, спектр власних значень енергії виявляється дискретним. Прикладом може служити фінітний (тобто обмежений) рух електрона в кулонівськім полі ядра атома Гідрогену. Дискретність енергетичних рівнів часток, замкнених в обмеженій області простору, випливає з двоїстої природи часток і є принциповою відмінністю квантової фізики від класичної.

Простою фізичною моделлю фінітного руху може служити рух частки в одномірній «потенціальній ямі» з нескінченно високими стінками. Частка не може залишити область розміром L. Вона рухається в цій області, зазнаючи багаторазових відбивань від стінок. З хвильової точки зору між стінками в зустрічних напрямках рухаються дві хвилі де Бройля. Це нагадує картину двох зустрічних хвиль, що біжать по струні із закріпленими кінцями. Як і у випадку струни, стаціонарним станам відповідають стоячі хвилі, які утворяться за умови, що на довжині L укладається ціле число півхвиль:

L = n · (λ / 2) (n = 1, 2, 3, ...) (87.1)

Таким чином, стаціонарним станам частки, замкненої в потенціальній ямі, відповідає дискретний набір довжин хвиль. Оскільки в квантово-механічному випадку довжина хвилі λ однозначно зв'язана з імпульсом частки: λ = h / p, а імпульс частки р визначає енергію її руху: E = p² / (2m) (нерелятивістське наближення), то квантованою (дискретною) виявляється й енергія частки. Квантово-механічний розрахунок приводить до наступного виразу:

. (87.2)

Тут m – маса частки,

h – постійна Планка,

E₁ = h² / (8m²) – енергія щонайнижчого стану.

Варто звернути увагу, що квантово-механічна частка на відміну від класичної не може спочивати на дні потенціальної ями, тобто мати енергію E₁ = 0. Це суперечило б співвідношенню невизначеностей

Δx · Δp_x ≥ h. (87.3)

Дійсно, у частинки, що знаходиться у стані спокою, імпульс строго дорівнює нулю, отже, Δp_x = 0. У той же час невизначеність координати частки Δx ~ L. Тому добуток Δx · Δp_x у частки, що лежить на дні потенціальної ями, повинен був би дорівнювати нулю.

Співвідношення невизначеностей дозволяє зробити оцінку мінімальної енергії E₁ частки. Якщо прийняти, що в стані з мінімальною енергією p_x ≈ Δp_x, то для мінімальної енергії E₁ отримуємо вираз:

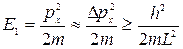. (87.4)

Ця груба оцінка дає правильне за порядком величини значення E₁.

Стоячі хвилі де Бройля, що утворяться під час руху частки в потенціальній ямі, це і є хвильові чи псі-функції, за допомогою яких квантова механіка описує стаціонарні стани мікрооб'єктів. Квадрат модуля |ψ|² хвильової функції визначається як ймовірність перебування частки в різних точках простору.

У комп'ютерній моделі можна змінювати ширину L потенціальної ями, а також масу m замкненої в ній частки. У лівому вікні висвічуються графічні зображення хвильових функцій ψ(x) чи квадратів їхніх модулів |ψ|² для декількох стаціонарних станів (n = 1–5). У правому вікні зображується енергетичний спектр частки, тобто спектр можливих значень її енергії. Зверніть увагу, що енергетичні рівні опускаються із збільшенням ширини L потенціальної ями і маси m замкненої в ній частки.

У комп'ютерній моделі маса частки виражається в масах протона m_p = 1,67·10^–27 кг. Отже, моделюються стани порівняно важких часток (ядер важких атомів), що опинились в потенціальній ямі із шириною порядку розмірів атомів.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
	\|	Хід роботи

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.