• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Частинка в одновимірній прямокутній потенціальній ямі. Проходження частинки через потенціальний бар’єр

7.4.1. Усякий зв’язаний стан частинки (вільний електрон в металі, нуклон в ядрі тощо), тобто стан з від’ємною потенціальною енергією, можна описати, ввівши поняття потенціальної ями. Розглянемо найпростіший випадок, коли частинка масою m перебуває в одновимірній прямокутній нескінченно глибокій потенціальній ямі шириною 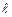. Оскільки початок відліку потенціальної енергії можна вибирати довільно, то задачу про “яму” замінимо задачею про “ящик”, на дні якого потенціальна енергія дорівнює нулю, а стінки якого нескінченно високі (рис. 7.6). Оператор Гамільтона 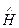(7.26) для цього випадку має вигляд

,

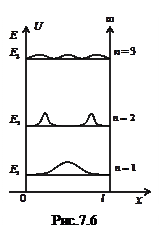
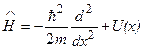де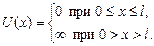

Всередині ящика рівняння Шрьодінгера (7.30) запишеться як

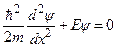
або

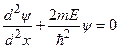. (7.32)

Введемо позначення

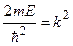, (7.33)

де k має зміст хвильового числа, якщо врахувати (7.31). Тоді (7.32) набуде форми, подібної (формально) до диференціального рівняння власних гармонічних коливань,

.

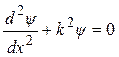Розв’язок цього рівняння шукаємо у вигляді гармонічної функції координати х:

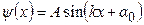. (7.34)

Оскільки хвильова функція повинна бути неперервною, в тому числі і на стінках ями, а вийти за межі ями частинка не може, то 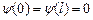. Перша гранична умова дає 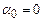, і тому

. (7.35)

Друга гранична умова дає

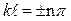, (7.36)

де n = 1, 2, 3, … – квантове число стану частинки.

Врахувавши, що 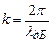, отримаємо з (7.36) співвідношення 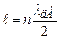, тобто в межах ширини ями повинно вкладатись ціле число півхвиль де Бройля.

Формальну амплітуду А в (7.35) знайдено з умови нормування хвильової функції до одиниці:

.

Звідси , і остаточно хвильова функція частинки в довільному квантовому стані n, з врахуванням (7.36), набуває вигляду

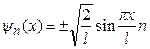. (7.37)

Об’єднуючи (7.33) і (7.36), отримаємо вираз для енергії частинки в різних квантових станах

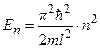. (7.38)

Отже, енергія частинки в потенціальній ямі приймає не довільні, а дискретні значення Е₁, Е₂, Е₃, …, зображені на рис. 7.6 відповідними енергетичними рівнями. Густина імовірності (рис. 7.6) залежить від координати частинки, при цьому по різному в кожному квантовому стані. Наприклад, для центру ями вона максимальна в стані n = 1 і дорівнює нулю в стані n = 2.

Відстань між сусідніми енергетичними рівнями

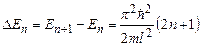. (7.39)

Розглядаючи електрон в атомі як такий, що перебуває в потенціальній ямі шириною , отримаємо 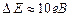, що співмірно з енергією електрона. В цей же час в макросвіті, коли m i l – дуже великі, відстань між енергетичними рівнями стає зникаюче малою, і квантуванням енергії можна знехтувати.

Задача про частинку в потенціальній ямі скінченної глибини розв’язується значно складніше, але висновок про квантування енергії і в цьому випадку залишається в силі.

7.4.2.Спорідненою до описаної є задача про проходження частинки через потенціальний бар’єр. Нехай мікрочастинка з масою m і енергією Е налітає на одновимірний прямокутний потенціальний бар’єр шириною l і висотою U₀ (рис. 7.7). Якщо частинка класична, то вона пролітає над бар’єром, коли Е > U₀, і відбивається від нього, коли Е < U₀. Проникнути під бар’єр класична частинка не може, бо тоді її кінетична енергія 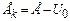була б меншою від нуля. Розв’язок рівняння Шрьодінгера для квантомеханічної мікрочастинки дає, що хвильові функції в усіх трьох областях 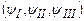відмінні від нуля, тобто мікрочастинка проникає під бар’єр і за бар’єр. Це явище називається тунелюванням. Від’ємні значення кінетичної енергії мікрочастинки в момент проходження бар’єру не можуть турбувати, бо в квантовій механіці кінетична енергія , як і потенціальна енергія, не є точно визначеними. Прозорість бар’єру, тобто імовірність тунелювання частинки, знаходиться як відношення густин імовірності в областях ІІІ та І. Розрахунок дає

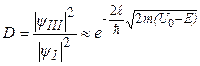. (7.40)

Звідси видно , що бар’єр тим прозоріший, чим менші його ширина і висота. Для класичної частинки (m ® ¥) і макробар’єру (l ® ¥) прозорість бар’єру зникаюче мала.

Читайте також:

1. Адміністративно-правове регулювання проходження державної служби
2. Акустичний контроль приміщень через засоби телефонного зв'язку
3. Алгоритм проходження графу вглиб
4. Аналіз ризику через моделювання.
5. БАР’ЄРИ В РОБОТІ З БАТЬКАМИ
6. Бар’єри простору і часу.
7. Бар’єри стратегічного планування та заходи щодо їх подолання
8. Бар’єри, які заважають ефективності педагогічного спілкування.
9. Бізнес через Internet
10. Біоелектричні явища в тканинах: будова мембран клітини, транспорт речовин через мембрану, потенціал дії та його розповсюдження.
11. В чому полягає явище тунелювання через потенціальний бар’єр, наведіть приклади.
12. В. Розрахунки через Інтернет

Переглядів: 4636