Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Ядерна модель атома. Борівський воднеподібний атом. Спектральні серії

Розділ 7. Елементи атомної фізики, квантової механіки і фізики твердого тіла

7.1.1. Оскільки світло випромінюється і поглинається атомами речовини, то виникає питання: яка структура атомів забезпечує дискретний (квантовий) характер вказаних процесів? Вперше конструктивну відповідь на це питання дав Резерфорд (1911р), досліджуючи розсіяння 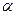-частинок на тонких (товщина » 1 мкм) металічних плівках (фольгах) (рис.7.1).

Центрований діафрагмою 2 пучок a-частинок від джерела 1 розсіювався фольгою 3 під різними кутами J від -p до p. Кількість a-частинок (Dn), розсіяних під фіксованими кутами, реєструвалась приймачем 4, який міг переміщуватись по колу навколо центру фольги. Було встановлено (рис.7.2):

а) більшість a-частинок, проходячи через фольгу, практично не розсіюється;

б) дуже добре виконується теоретично передбачуване співвідношення

в) певна, хоч і незначна, кількість a-частинок розсіюється під кутами, близькими до ±p.

Аналіз результатів експерименту дозволив Резерфорду запропонувати ядерну модель атома, згідно з якою в центрі атома 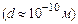розміщене позитивно заряджене ядро , що володіє масою, приблизно рівною масі атома. Навколо ядра рухаються електрони. Якщо в нейтральному атомі Z електронів, де Z – порядковий номер елементу в періодичній таблиці елементів Д.І. Менделєєва, то заряд ядра , де 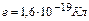– елементарний заряд. В рамках цієї моделі зрозуміло, що ймовірність лобового зіткнення a-частинки з ядром, яке забезпечує розсіяння на кути ±p, дуже мала. Електрони ж в силу незначної маси розсіювати a-частинки не можуть.

Оскільки, у відповідності з теоремою Ірншоу, неможлива стійка статична конфігурація електричних зарядів, то атом мусить бути динамічною системою, тобто електрони повинні рухатись навколо ядра по замкнених (колових чи еліптичних) орбітах. Такий рух є прискореним, і електрон з точки зору класичної фізики повинен втрачати енергію, випромінюючи електромагнітні хвилі, і тому впасти на ядро. Але, як відомо, атом – стійка конфігурація електричних зарядів. І тому, приймаючи ядерну модель атома, потрібно відмовитись від класичного опису орбітального руху електронів.

7.1.2. Розвиваючи запропоновану модель, у 1913 р. Н. Бор висунув гіпотезу у вигляді наступних постулатів: а) із усіх можливих механічних станів (орбіт) електрона в атомі здійснюються лише такі, для яких момент імпульсу орбітального руху електрона кратний до постійної Планка h, тобто

, (7.1)

де 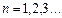– квантове число стану (номер орбіти), а – постійна Дірака; такі стани називаються стаціонарними;

б) перебуваючи в стаціонарному стані, електрон атома не випромінює і не поглинає енергії;

в) при переході з одного стаціонарного стану на інший електрон випромінює чи поглинає квант світла з енергією, рівною різниці енергій цих станів, тобто

. (7.2)

Отже, основна ідея постулатів Бора полягає в квантуванні (дискретності) механічних характеристик руху електронів: моменту імпульсу, енергії тощо. Рис.7.3 ілюструє наявність стаціонарних квантових станів (енергетичних рівнів) з енергіями та 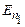і випромінювальні та поглинальні переходи між ними: зменшення енергії електрона супроводжується випромінюванням кванту світла (фотона) з енергією 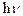; поглинання кванту світла з енергією 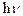забезпечує збільшення енергії електрона від 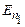до . В цій моделі випромінювання (поглинання) квантів світла з енергіями є неможливим.

7.1.3. Запропонована теорія вперше була застосована до воднеподібних атомів (тощо), в яких навколо ядра, заряд якого 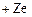, рухається по коловій орбіті радіусом r лише один електрон. При цьому ядро вважається нерухомим. Розглядаючи електрон як класичну матеріальну точку, енергію атома запишемо як суму кінетичної і потенціальної енергій електрона в кулонівському полі ядра

, (7.3)

де m – маса електрона, – електрична стала. Врахуємо, що в ролі доцентрової сили, яка забезпечує коловий рух електрона, виступає кулонівська сила, тобто

. (7.4)

Звідси випливає, що , і (7.3) запишеться у вигляді

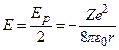. (7.5)

Оскільки орбітальний момент імпульсу електрона

то, врахувавши (7.4), отримаємо вираз для радіуса стаціонарної орбіти електрона

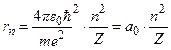, (7.6)

де 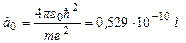має зміст радіуса першої (n = 1) орбіти електрона в атомі водню (Z = 1); ця величина називається борівським радіусом. Отже, має місце квантування (n = 1, 2, 3, …) радіусів стаціонарних орбіт електрона.

Підставляючи (7.6) у (7.5), отримаємо вираз для енергії атома

. (7.7)

Введемо позначення: 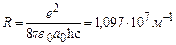– постійна Рідберга. Тоді (7.7) набуде остаточного вигляду

. (7.8)

Отже, енергія атома приймає дискретні значення, тобто квантується. Стан з найнижчою енергією (n = 1) називається основним, усі інші стани – збудженими. Стан з найвищою енергією (n = ¥) відповідає іонізації атома. Отже, енергія іонізації воднеподібних атомів

, (еВ).

І тому зручно інколи (7.8) записувати у вигляді

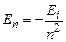. (7.9)

7.1.4.Зобразимо енергетичну діаграму атома водню (Z = 1) (рис.7.4). В основному стані атом може перебувати як завгодно довго. Якщо ж його перевести певним чином (теплом, світлом, бомбардуванням вільними електронами тощо) в довільний збуджений стан, то тривалість перебування в цьому стані складає , і атом самовільно переходить в основний чи нижчі збуджені стани, як показано на рис. 7.4. При цьому, у відповідності з (7.2) та (7.8), випромінюється фотон з енергією

а довжина випромінюваної світлової хвилі розраховується за серіальною формулою Бальмера

, (7.10)

де n₂ – квантове число стану, з якого відбувається перехід, n₁ – квантове число стану, в який переходить атом.

Якщо забезпечити умови “заселеності” усіх збуджених станів, то в спектрі випромінювання атомарного водню спостерігатиметься значна кількість спектральних ліній, які можна згрупувати в наступні серії:

І–серія Лаймана, для якої а ;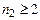

ІІ–серія Бальмера, для якої 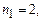а ;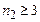

ІІІ–серія Пашена, для якої а ;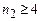

ІV–серії Брекета, для якої 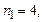а 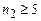, тощо.

Лінії серії Лаймана лежать в ультрафіолетовій області, серії Бальмера – у видимій області, серії Пашена, Брекета – в інфрачервоній області. Відмітимо, що довжини хвиль, розраховані за формулою (7.10), дуже добре співпадають з експериментальними значеннями.

На цьому тріумф теорії Бора закінчується, бо вона виявилась нездатною пояснити спектри випромінювання складних (неводнеподібних) атомів, а також інтенсивності спектральних ліній навіть атомарного водню. Слабкість цієї теорії полягає в тому, що, ввівши нехарактерні для класичної фізики поняття про квантування фізичних величин і про квантові переходи (”стрибки”), в усьому іншому вона залишилась класичною. І тому послідовна, квантовомеханічна теорія повинна ґрунтуватись на нових (некласичних) принципах опису стану і руху мікрочастинок.

§7.2. Корпускулярно-хвильовий дуалізм матерії; гіпотеза де Бройля. Співвідношення невизначеностей Гайзенберга

7.2.1. Як показано в розділі 6, світло володіє як хвильовими, так і корпускулярними властивостями. Луї де Бройль (1924 рік) висунув гіпотезу (постулат) про те, що корпускулярно-хвильовий дуалізм притаманний не тільки світлу, але матерії взагалі: усяка частинка, яка має імпульс і енергію Е, володіє хвильовими властивостями, її рух супроводжується хвильовим процесом з довжиною хвилі де Бройля

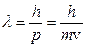(7.11)

та частотою

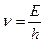. (7.12)

В залежності від величини швидкості v (кінетичної енергії 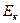) частинок, їх імпульс розраховується або за класичною формулою (при )

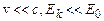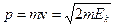, (7.13)

або за релятивістською формулою (при 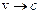, Е_k співмірна з Е₀)

, (7.14)

де m – маса частинки (таблична величина), – її енергія спокою.

Зокрема, вільна частинка, що рухається вздовж осі х, описується плоскою хвилею де Бройля

, (7.15)

де 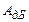– амплітуда хвилі де Бройля, – її циклічна частота, – її хвильове число. Фазова швидкість хвиль де Бройля

, (7.16)

а групова швидкість

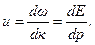(7.17)

Борівське квантування моменту імпульсу орбітального руху електрона набуває нового змісту з врахуванням хвильових властивостей електрона. Зокрема, довжина стаціонарної орбіти

тобто в межах орбіти вкладається ціле число хвиль де Бройля.

Оцінимо довжину хвилі де Бройля електрона, який прискорився електричним полем 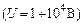. Саме такі напруги використовуються у вакуумних електронних приладах (радіолампи, рентгенівські трубки тощо). Підставляючи в формулу (7.13) значення кінетичної енергії електронів 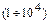еВ, отримаємо за (7.11) для довжин хвиль де Бройля 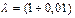нм.

Відомо, що найбільш чітко хвильові властивості світла проявляються в явищі дифракції. І тому прояв хвильових властивостей електронних (нейтронних, атомних тощо) пучків слід очікувати в цьому ж явищі. При цьому чітка дифракційна гратка спостерігається тоді, коли довжини хвиль співмірні з розміром дифракційної неоднорідності (отвори, щілини тощо).

Розміри макроприладів значно перевищують довжини хвиль де Бройля електронів, і тому в цьому випадку хвильові властивості електронів явно не відслідковуються. В цей же час розраховані значення l співмірні з розміром (нм) кристалічної решітки твердих тіл. І тому така решітка повинна бути дифракційним пристроєм для електронних пучків. Дійсно, при проходженні електронних пучків через тонкі полікристалічні плівки та при їх відбиванні від монокристалів спостерігається така ж дифракційна картина, як і при взаємодії рентгенівських променів з твердими кристалічними тілами. Зокрема, виконується закон Вульфа-Бреггів (див. розділ 6), встановлений для рентгенівських променів. Дифракція нейтронних пучків також виявлена експериментально і використовується для наукових досліджень.

Відмітимо, що довжини хвиль де Бройля макроскопічних тіл, за рахунок великої маси, настільки малі, що їх хвильові властивості виявити неможливо.

7.2.2. Корпускулярно-хвильовий дуалізм частинок в мікросвіті накладає обмеження на можливості класичного опису їх стану. В класичній механіці стан частинки задається сукупністю точно заданих координат (x,y,z) та проекцій вектора імпульсу . Якщо задані сили, що діють на частинку, то можна, користуючись законами класичної механіки, передбачити її стан в довільний момент часу – класичний принцип причинності. Для частинки, що рухається вздовж осі х, це означає, що неточності (невизначеності) координати та імпульсу 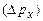рівні нулю і добуток .

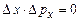Абсолютно інша ситуація в мікросвіті. Дійсно, вільна частинка, яка рухається вздовж осі х, описується плоскою монохроматичною 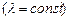хвилею де Бройля (7.15), де . І тому її положення повністю невизначене, тобто 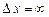. З іншого боку, імпульс такої частинки 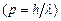строго визначений і 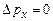. А отже, добуток є математично невизначеним .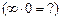

В мікросвіті можна змоделювати об’єкти (наприклад, хвильовий пакет), для яких координата точно визначена , але імпульс повністю невизначений 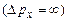, і тому має місце математична невизначеність типу

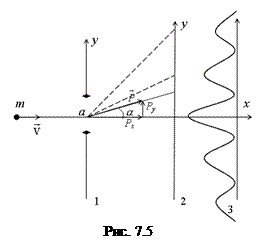
Для того, щоб дещо прояснити цю ситуацію, розглянемо наступний умовний експеримент (рис. 7.5). Нехай мікрочастинки, що рухаються вздовж осі х, пролітають через щілину шириною а в непрозорому екрані (1) і фіксуються на екрані спостереження (2). Після проходження щілини розподіл мікрочастинок вздовж осі у повинен відтворювати розподіл інтенсивності в дифракційній картині (3): центральний і бічні максимуми розділені мінімумами. До щілини невизначеності координати та імпульсу: 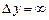, . В момент проходження щілини: , 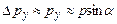. Якщо розглядати лише мікрочастинки, які попадають в центральний максимум, що обмежений першими мінімумами, то 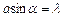, і тому . Добуток невизначеностей:

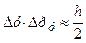На підставі аналізу подібних умовних експериментів Гайзенберг (1927р.) встановив співвідношення між невизначеностями координат і відповідних імпульсів у вигляді

. (7.18)

Інтерпретацію цих співвідношень дав Н. Бор у вигляді принципу доповнюваності:

1) інформація про стан мікрочастинок може бути отримана лише за допомогою макроприладів, які взаємодіють з мікрочастинками;

2) за допомогою конкретного макроприладу можна встановити точне значення або координати, або імпульсу; при цьому чим точніше задана одна характеристика, тим більш невизначена інша.

Стосовно електрона в атомі співвідношення Гейзенберга означають, що поняття орбіти втрачає зміст. Дійсно, якщо невизначеність швидкості електрона , то невизначеність координати , що співмірно з розміром атома. Таким чином, електрон “розмазаний” по всьому об’ємі атома. В цей же час співвідношення невизначеностей не накладають суттєвих обмежень на класичний опис стану макротіл. Дійсно, оскільки 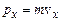, то 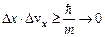навіть при .

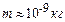Пара “координата-імпульс” у співвідношенні (7.18) не є випадковою, оскільки вона входить як добуток в рівняння плоскої хвилі де Бройля (7.15), записане у вигляді

. (7.19)

І тому слід очікувати, що і для іншої пари “енергія-час” матиме місце співвідношення невизначеностей

, (7.20)

де має зміст тривалості перебування (часу життя) мікрочастинки в певному стані. Зокрема, для основного стану електрона у воднеподібному атомі 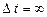і тому 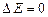, тобто енергетичний рівень основного стану нерозмитий. Для збуджених станів і . За рахунок цього спектральні лінії випромінювання не є строго монохроматичними.

§7.3. Хвильова функція та її зміст. Рівняння Шрьодінгера

7.3.1. Корпускулярно-хвильовий дуалізм матерії встановлює межі застосування класичної фізики. В мікросвіті класичний спосіб опису стану частинок за допомогою координат та імпульсів перестає бути однозначним і повинен бути замінений іншим – статистичним способом, на якому грунтується механіка мікросвіту – квантова механіка.

Стан мікрочастинок в квантовій механіці задається хвильовою функцією . Зокрема, для вільної одновимірної частинки хвильовою функцією є плоска хвиля де Бройля (7.19), яку представимо тут у комплексній формі:

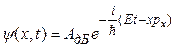, (7.21)

де 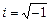. Помноживши 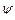на комплексно спряжену функцію 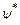, отримаємо

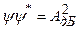. (7.22)

З точки зору хвильових уявлень квадрат амплітуди хвилі визначає її інтенсивність, зокрема, інтенсивність дифракційних максимумів на рис. 7.5. З точки зору корпускулярних уявлень – це імовірність попасти мікрочастинці в ту чи іншу точку екрану спостереження після проходження щілини. Отже, фізичний зміст має не сама хвильова функція, а вираз , який називається густиною імовірності. Для частинок, які не є вільними, а перебувають в силових полях, хвильова функція не може розглядатися як просторова хвиля, але її ймовірнісна інтерпретація залишається в силі. Зокрема, імовірність знайти мікрочастинку в деякій області простору, наприклад, в елементарному об’ємі , становить

. (7.23)

Оскільки імовірність повинна бути однозначною, неперервною і скінченою, то на хвильову функцію накладаються наступні стандартні вимоги:

1) вона повинна бути однозначною, неперервною і скінченою;

2) перші похідні по координатах і часу від хвильової функції також повинні бути неперервними, що забезпечить “гладкість” імовірності;

3) вона повинна бути інтегрованою; зокрема, 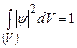, як імовірність знайти частинку в будь-якій точці простору V (імовірність вірогідної події).

Знання хвильової функції дозволяє встановити середнє значення довільної фізичної величини f:

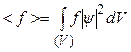. (7.24)

Для знаходження хвильової функції конкретного квантовомеханічного об’єкту необхідно розв’язати рівняння Шрьодінгера (1926 р.)

, (7.25)

яке є аналогом ІІ закону Ньютона класичної механіки. В цьому рівнянні

– (7.26)

оператор Гамільтона або оператор повної енергії частинки, де m – маса частинки, 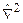– оператор Лапласа

, (7.27)

U – оператор потенціальної енергії, дія якого зводиться до простого множення на хвильову функцію.

Якщо потенціальна енергія частинки явно не залежить від часу, тобто , то квантовомеханічна задача називається стаціонарною, і у хвильовій функції можливе розділення змінних, тобто

. (7.28)

Підставляючи (7.28) у (7.25), після нескладних перетворень отримаємо

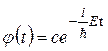, (7.29)

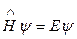, (7.30)

де с і Е – константи інтегрування, при цьому Е має зміст енергії частинки.

Рівняння (7.30) називається рівнянням Шрьодінгера для стаціонарних станів. Розв’язок цього диференціального рівняння задовольняє стандартні вимоги до хвильової функції, як правило, не при усяких, а дискретних (дозволених) значеннях параметра Е. Ці значення називаються власними значеннями оператора 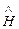, а відповідні хвильові функції 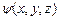– власними функціями цього оператора.

Отже, розв’язок рівняння Шрьодінгера (7.30) зводиться до знаходження власних значень і власних функцій оператора повної енергії частинки 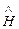. При цьому дискретність (квантування) енергії не вимагає додаткових штучних припущень типу постулатів Бора (§7.1), а витікає з математичних властивостей самого рівняння Шредінгера. Фізична ж суть цього рівняння полягає у виборі аналітичної форми потенціальної енергії U, тобто у виборі моделі квантомеханічного об’єкту.

7.3.3. Для вільної (U=0) частинки, що рухається вздовж осі х, стаціонарне рівняння Шрьодінгера має вигляд

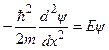Розв’язок цього рівняння шукається у вигляді

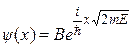що легко перевірити підстановкою в рівняння Шрьодінгера.

Повна хвильова функція, з врахуванням (7.28) і (7.29),

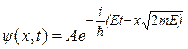
співпадає з виразом для плоскої хвилі де Бройля (7.19), якщо покласти, що 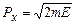. Остання рівність є очевидною, оскільки повна енергія частинки співпадає з її кінетичною енергією

. (7.31)

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Гальмівне рентгенівське випромінювання	\|	Частинка в одновимірній прямокутній потенціальній ямі. Проходження частинки через потенціальний бар’єр

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.04 сек.