• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Квантовий лінійний гармонічний осцилятор

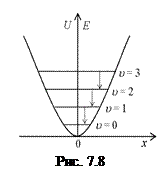
7.5.1. Лінійний гармонічний осцилятор – це матеріальна точка, яка здійснює одновимірний (вздовж осі х) рух під дією квазіпружної сили . Потенціальна енергія осцилятора (рис. 7.8)

, (7.41)

де m – маса осцилятора, – його власна циклічна частота, х – зміщення від положення рівноваги. Отже, мова піде про мікрочастинку, яка перебуває в потенціальній ямі з параболічними стінками. Підставляючи (7.41) в рівняння Шрьодінгера (7.30), отримаємо

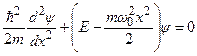. (7.42)

Власні хвильові функції, тобто розв’язки цього рівняння, які задовольняють стандартні вимоги (§7.3), мають вигляд

, (7.43)

де 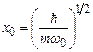, – поліноми Чебишева-Ерміта u-го порядку, 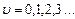– коливаль­не квантове число.

Для класичного осцилятора зміщення х обмежене амплітудою коливань 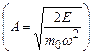; для квантового осцилятора таке обмеження знімається за рахунок можливості тунелювати через стінки потенціальної ями. А це означає, що існує ненульова імовірність знайти мікрочастинку поза ямою.

Власні значення оператора Гамільтона для квантового осцилятора

. (7.44)

Тут враховано, що 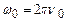. Отже, енергія квантового осцилятора приймає дискретні значення , тобто квантується (рис.7.8). Найменша енергія квантового осцилятора, так звана нульова енергія, на відміну від класичного осцилятора, не дорівнює нулю. Наявність нульових коливань підтверджується експериментально в дослідах по розсіянню світла в кристалах при дуже низьких температурах, коли з точки зору класичної фізики коливальний рух кристалічної гратки повинен би припинитися.

Перебуваючи в стаціонарному стані, квантовий осцилятор не поглинає і не випромінює енергії. Випромінювання (поглинання) світла відбувається при переході осцилятора між стаціонарними станами, при цьому квантова механіка дозволяє лише переходи між сусідніми енергетичними рівнями, тобто 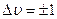(правило відбору). Енергія випромінюваного (поглинутого) кванту , що підтверджує квантовий постулат Планка.

Читайте також:

1. Лінійний SVM
2. Лінійний напружений стан
3. Лінійний оператор та його матриця
4. Нелінійний підхід
5. Порядок Осциляторіальні - Oscillatoriales
6. Правила аналізу осциляторів
7. Рівноприскорений прямолінійний рух. Прискорення.
8. Середньоарифметичний і середньогармонічний індекси

Переглядів: 1745