• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Лінійний оператор та його матриця

Означення. Лінйним оператором у векторному просторі називається відображення векторного простору в себе 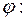→таке, що виконані наступні умови (умови лінійності):

1) ;

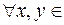
1) ;

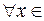
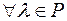
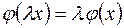Лінійний оператор називається також лінійним перетворенням векторного простору . Лінійні перетворення є гомоморфізмами.

З означення безпосередньо випливають наступні

Найпростіші властивості лінійного оператору:

1) Образом нуль-вектора є нуль-вектор: .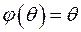

2) Образом вектора, протилежного довільному вектору 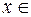є вектор, протилежний образу вектора :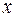

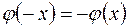
3) Образом лінійної комбінації довільних векторів 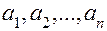простору є лінійна комбінація (з тими ж коефіцієнтами) образів цих векторів:

Приклади лінійних операторів:

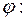
1) →: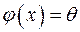– нульовий оператор. Позначається .

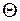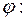
2) →: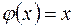– тотожний (одиничний) оператор. Позначається .

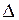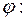
3) →– поворот площини навколо початку координат на кут 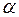в додатному напрямку.

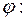
4) 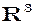→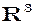– ортогональне проектування векторів на деяку площину.

5) Нехай 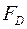– векторний простір функцій, диференційованих на всій числовій прямій. Розглянемо перетворення 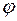простору 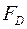, яке кожній функції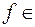 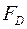ставить у відповідність її похідну, тобто 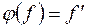. За властивостями похідної 1) 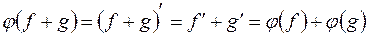і

2) .

Таким чином, диференціювання – лінійний оператор в .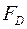

6) Нехай 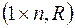– векторний простір числових рядків, 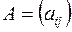– матриця порядку 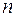з дійсними елементами. Перетворення простору 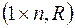, яке кожному вектору 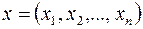ставить у відповідність вектор 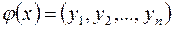, координати якого визначаються за формулою 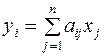, тобто 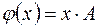є лінійним оператором.

Нехай у векторному просторі заданий деякий базис .

Означення. Матрицею лінійного оператора 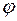в базисі називається матриця

,

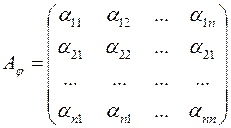елементами якої є коефіцієнти в розкладі образів векторів за базисом , тобто

;

;

………………………………………..

.

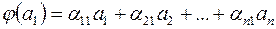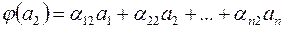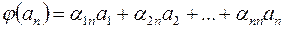З означення випливає, що стовпцями матриці 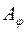є координатні рядки векторів 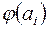, , 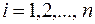в базисі .

Приклади.

1) Матрицею тотожного оператора є одинична матриця: ,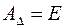

2) Матрицею нульового оператора є нульова матриця .

При фіксованому базисі кожному лінійному оператору 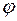простору відповідає певна матриця 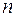-го порядку – матриця цього лінійного оператора 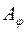. Справедливе і обернене: кожна матриця 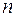-го порядку є матрицею певного лінійного оператора простору в базисі .

У координатному вигляді дія лінійного оператора 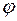на вектор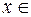 зводиться до множення матриці лінійного оператора 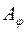на координатний стовпчик вектора :

.

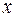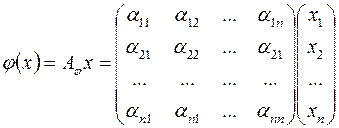Ясно, що матриця оператора 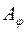залежить від вибору базису простору .

Читайте також:

1. Арифметичні оператори
2. Арифметичні цикли. Оператор циклу For – Next
3. Базовий синтаксис деяких основних операторів
4. Блочна матриця.
5. Використання оператора throw
6. Дiї над матрицями
7. Дії над матрицями
8. Дії над матрицями
9. ЕВОЛЮЦІЙНА МАТРИЦЯ ДЛЯ СХІДНОЇ ЄВРОПИ
10. Загальні вимоги до робочого місця оператора ЕОМ
11. Запис SQL-операторів
12. Заява про видачу ліцензії на бланку встановленої форми (згідно з додатком 1 до пункту 1.2.4 Ліцензійних умов провадження туроператорської та турагентської діяльності (додаток 1).

Переглядів: 8122