• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник

Підпростори векторного простору

Означення. Непорожня підмножина 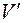векторного простору 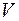називається підпростором простору 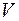, якщо воно є векторним простором відносно операцій, визначених в .

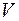Це означає, що множина 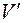задовольняє аксіомам векторного простору, якщо додавати його елементи і множити їх на числа з поля 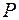(над яким заданий векторний простір 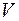) так, як це визначено для елементів простору .

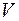Теорема (критерій підпростору). Непорожня підмножина 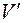векторного простору 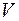є підпростором простору 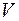оді і тільки тоді, коли виконується наступні умови:

1) Якщо , то ;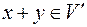

2) Якщ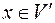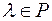о , то .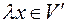

Кожний підпростір будь-якого векторного простору саме по собі є векторним простором. тому всі поняття, які були введені для просторів (розмірність, базис та ін.) розповсюджуються і на підпростори.

Теорема (про розмірність підпростору). Розмірність будь-якого підпростору векторного простору не більше розмірності простору.

Приклади підпросторів.

1) Множина 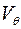, яка містить тільки нульовий елемент 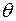є підпростором будь-якого векторного простору. Його називають нульовим підпростором. В нульовому підпросторі нема лінійно незалежних систем векторів. Його базис – порожня множина. Його розмірність вважають нульовою.

2) Будь-який векторний простір 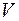є своїм підпростором.

Нульовий підпростір 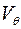і сам простір 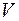звичайно називають невласними підпросторами.

3) В арифметичному числовому векторному просторі 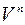множина 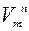, , 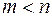векторів вигляду 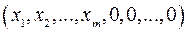є підпростором.

4) Векторний простір многочленів з коефіцієнтами з поля 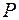є підпростором векторного простору функцій, неперервних на відрізку 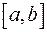, якщо многочлени вважати заданими на відрізку .

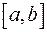5) У векторному просторі 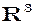геометричних векторів підпросторами будуть вусі площини і всі прямі, що проходять через початок координат.

6) Лінійні оболонки є цікавим прикладом підпростору. Нехай 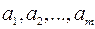– довільна система векторів простору 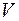. Множина всіх векторів, які є лінійними комбінаціями векторів системи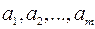є підпростором простору 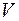, який позначається 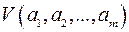і називається лінійною оболонкою векторів 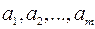, або підпростором, натягнутим на вектори .

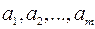Читайте також:

1. V. Антропогенне забруднення навколоземного простору.
2. Аналіз паралельного інтерейсу з DSP-процесорами: запис даних в ЦАП, що під’єднаний до адресного простору пам’яті
3. Аналіз паралельного інтерфейсу з DSP-процесорами: читання даних з АЦП, що під’єднаний до адресного простору пам’яті
4. Бар’єри простору і часу.
5. Векторного простору
6. Властивості векторного добутку.
7. Властивості простору і часу у класичній механіці
8. Вплив кольору на сприйняття простору
9. Доповнення простору.
10. Єдність матерії, руху, простору і часу.
11. Єдність матерії, руху, простору і часу.
12. Єдність матерії, руху, простору і часу.

Переглядів: 4540