Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Взаємозв'язок між тензорами напруг і деформацій. Узагальнений закон Гука

Залежності між напругами й деформаціями носять фізичний характер. Обмежуючись малими деформаціями, зв'язок між напругами й деформаціями можна вважати лінійним (рис.1.6).

Рис.1.6. Діаграма розтягування сталі

В загальному випадку анізотропії кожна складова напруги може залежати від усіх складових деформації:

(1.58)

Коефіцієнти (загальним числом 36) називаються пружними постійними. Якщо розглядати тільки пружні процеси деформування, при яких після зняття навантажень форма й розміри тіла повністю відновлюються, то між коефіцієнтами існує залежність:

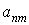Тоді число пружних постійних зменшується до 21.

Для ізотропного тіла рівняння (1.58) не повинні змінюватися при будь-яких перетвореннях координат. Здійснюючи поворот осей на 180^с, можна встановити, що нормальні напруги не пов'язані з кутовими деформаціями, а дотичні — з лінійними, що знижує кількість пружних постійних до 12. Крім того, дотичні напруги не пов'язані із пружними деформаціями в інших площинах, а це зменшує кількість пружних постійних до дев'яти. Нарешті, після повороту осей на 90^° і на довільний кут число пружних постійних стає рівним двом, які відомі з курсу опору матеріалів.

При випробуванні стержня на розтягання встановлена пропорційна залежність між нормальною напругою й лінійною деформацією в одному напрямку, що називається законом Гука:

(1.59)

де пружна постійна називається модулем повздовжньої пружності.

Тим же експериментальним шляхом установлений зв'язок між лінійними деформаціями в повздовжньому й поперечному напрямках:

(1.60)

де — лінійна деформація в поперечному напрямку, — другим пружним постійним, називаним коефіцієнтом Пуассона.

При механічних випробуваннях на чистий зсув встановлена прямо пропорційна залежність між дотичним напруженням і кутовою деформацією в площині дії цієї напруги, що одержала назву закону Гука при зсуві:

(1.61)

де величина 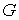є третьої пружною постійною й називається модулем зсуву. Однак ця пружна постійна не є незалежною, тому що пов'язана з першими двома залежностями

(1.62)

Щоб установити залежності між складовими деформації й напругами, виділимо з тіла нескінченно малий паралелепіпед (рис.1.1) і розглянемо дію тільки нормальних напруг Різницею між напругами на протилежних гранях паралелепіпеда можна зневажити, тому що вона приводить до деформацій більш високого порядку малості.

Визначимо подовження ребра 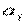паралельного напрузі При дії цієї напруги відповідно до закону Гука (1.59) відбудеться відносне подовження ребра

Напруга викликає аналогічне подовження в напрямку, перпендикулярному ребру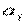

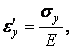
а в напрямку самого ребра - укорочення, що згідно (1.60) становить

або, з урахуванням виразу деформації

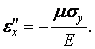
Аналогічно визначається відносне вкорочення ребра при дії напруги

На підставі принципу незалежності дії сил повне відносне подовження ребра можна визначити як суму подовжень від дії кожної напруги:

або

Аналогічно можна визначити лінійні деформації по напрямках двох інших осей:

Відповідно до закону Гука при зсуві (1.61) зв'язок між кутовими деформаціями й дотичними напруженнями можна представити незалежно для кожної із трьох площин, паралельних координатним площинам:

Таким чином, отримані шість формул, які виражають лінійну залежність між складовими деформації й напруг в ізотропному пружному тілі й називаються узагальненим законом Гука:

(1.63)

Залежності (1.63) виражають деформації через напруги, але при розв’язанні задач іноді виявляється необхідним виразити напруги через деформації.

У якості допоміжних виведемо попередньо співвідношення для об'ємної деформації. Складемо почленно перші три формули (1.63):

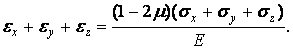
(1.64)

На підставі (1.15) і (1.39)

тому (1.64) можна представити у вигляді

(1.65)

тобто відносна об'ємна деформація пропорційна першому інваріанту напруженого стану.

Введемо в розгляд модуль об'ємного розширення

(1.66)

тоді

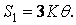
(1.67)

Враховуючи, що

(1.68)

перший інваріант напруженого стану можна замінити потроєною середньою напругою в точці, і замість (1.67) одержимо

(1.69)

Отже, середня напруга в точці пропорційно об'ємній деформації.

Щоб виразити напруги через деформації додамо й віднімемо в квадратних дужках першої формули (1.63) величину

або, виділяючи перший інваріант напруженого стану згідно (1.15),

Підставляючи з (1.65), одержимо

звідки

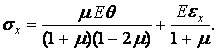
(1.70)

Введемо позначення

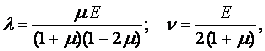
(1.71)

тоді (1.70) приймає вид

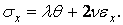
(1.72)

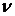Пружні постійні й характеризують пружні властивості матеріалу й називаються коефіцієнтами Ламі. Порівнюючи (1.62) і (1.71), можна зробити висновок, що

Аналогічним чином можна одержати вираз для й 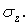Ці три залежності й останні три формули (1.63), записані відносно дотичних напруг, втворять шість співвідношень, які називаються зворотною формою узагальненого закону Гука:

(1.73)

Складемо почленно перші три формули (1.73):

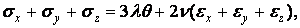
або, з врахуванням (1.15) і (1.39),

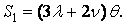
(1.74)

Це співвідношення встановлює зв'язок між першими інваріантами напруженого й деформованого станів через постійні Ламе.

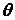Знову заміняючи перший інваріант напруженого стану потроєною середньою напругою в точці а об'ємну деформацію — потроєною середньою деформацією точки, одержимо ще одну форму закону Гука:

(1.75)

<== попередня сторінка	\|	наступна сторінка ==>
Тензор деформацій. Головні деформації	\|	Робота пружних сил. Потенційна енергія деформацій

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.