• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Робота пружних сил. Потенційна енергія деформацій

Виділимо з тіла нескінченно малий паралелепіпед (рис.1.1) і визначимо роботу, що виконується прикладеними до нього пружними силами на можливих переміщеннях.

Розглянемо роботу, що виконують нормальні сили, що діють на гранях паралелепіпеда, перпендикулярних осі 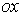й відповідних нормальним напругам і 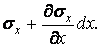Якщо точкам тіла надати які-небудь можливі переміщення, то відстань між розглянутими гранями зміниться на величину 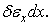Відкидаючи у виразі для напруги на правій грані величину 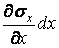як нескінченно малу в порівнянні зі 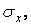знаходимо, що дві протилежні рівні сили 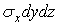виконують роботу

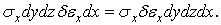
Аналогічно визначається робота нормальних сил в напрямках осей 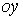і 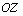на відповідних їм можливих переміщеннях:

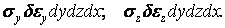
Дотичні сили, паралельні осі 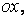на вертикальних гранях (при відкиданні нескінченно малих величин вищого порядку малості) утворять пари сил з моментом 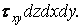Для обчислення роботи, що виконує ця пара на можливих переміщеннях, її момент потрібно помножити на збільшення відповідного кута зсуву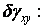

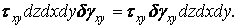
У такий же спосіб визначається робота двох інших дотичних складових на відповідних їм можливих переміщеннях:

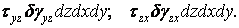
На підставі принципу незалежності дії сил можливу роботу всіх сил, прикладених до розглянутого елемента, одержимо як суму можливих робіт, виконуваних кожною силою окремо:

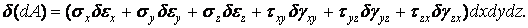
Розділивши цей вираз на об’єм розглянутого паралелепіпеда dxdydz, одержимо збільшення роботи, віднесеної до одиниці об'єму тіла в тій точці, де виділений паралелепіпед:

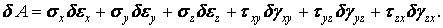
(1.76)

На підставі закону збереження енергії будемо вважати, що робота пружних сил повністю переходить у потенційну енергію, що накопичується тілом при одержанні пружних деформацій і повертаєму їм назад у вигляді роботи сил при зникненні деформації.

Якщо позначити через W питому потенційну енергію, тобто енергію, що накопичується в одиниці об'єму деформуємого тіла, то на підставі прийнятого вище допущення збільшення роботи внутрішніх сил на можливих переміщеннях повністю перейде в потенційну енергію й остання одержить збільшення

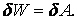
Порівнюючи це співвідношення з формулою (1.76), одержуємо збільшення питомої потенційної енергії в такому вигляді:

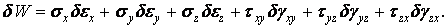
(1.77)

Збільшення 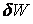з точністю до величин другого порядку малості можна замінити повним диференціалом:

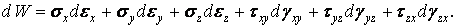
Підставляючи сюди значення напруг (1.73), одержуємо

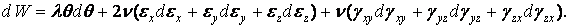
Інтегруючи, знайдемо вираз потенційної енергії через деформації:

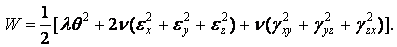
(1.78)

Виконуючи зворотну операцію з формулами (1.73), одержимо

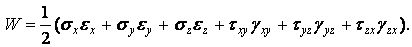
(1.79)

Отже, питома потенційна енергія, що накопичується в пружному тілі, дорівнює напівсумі добутків складових напруг на відповідні їм складові деформації. Це співвідношення називають формулою Клапейрона.

Питому потенційну енергію можна також виразити тільки через складові напруг. Підставляючи у формулу (1.79) значення деформацій (1.63), знайдемо

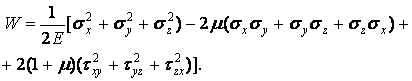
(1.80)

Відповідно до співвідношень (1.71), пружні постійні й 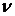, що входять у формулу (1.78), позитивні, отже, потенційна енергія також завжди є величиною позитивною.

Потенційну енергію, що накопичується у всьому тілі, підраховують підсумовуванням питомої потенційної енергії по всьому об’ємі тіла V:

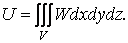
(1.81)

Підставляючи сюди вираз питомої потенційної енергії по формулі Клапейрона (1.79), остаточно одержуємо

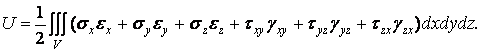
(1.82)

Читайте також:

1. II. Будова доменної печі (ДП) і її робота
2. II. Критерій найбільших лінійних деформацій
3. II. Самостійна робота студентів.
4. IV. ВИХОВНА РОБОТА В КЛАСІ
5. IV. ІНДИВІДУАЛЬНА РОБОТА СТУДЕНТІВ.
6. IV. Науково-дослідницька робота.
7. IV. Практична робота.
8. IV. Робота над темою уроку
9. Qорганізаційне середовище, в якому виконується робота
10. R – розрахунковий опір грунту основи, це такий тиск, при якому глибина зон пластичних деформацій (t) рівна 1/4b.
11. V. Робота з підручником
12. V. Робота з підручником. с. 59-60

Переглядів: 611