Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Стискання клина

Задача про стискання клина зосередженою силою, прикладеної до вершини (рис. 4.5), можна розглядати як окремий випадок задачі, розібраної в 4.3, коли .

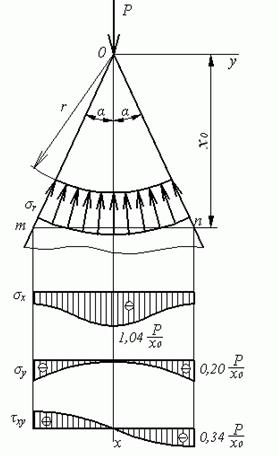
Рис. 4.5. Стискання клина зосередженою силою

При цьому постійні 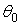й 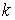відповідно до формул (4.9) і (4.10) приймають наступні значення:

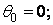
(4.11)

Вносячи ці значення у формули (4.8), одержуємо такі складові напружень:

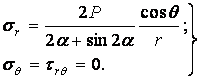
(4.12)

Епюра радіальних напружень 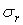у перерезі 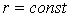показана на тому ж малюнку.

Для дослідження напруженого стану в стиснутому клині зручно перейти до його поперечних і поздовжніх перерезів. Якщо вісь сполучити з віссю симетрії клина, а вісь 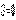направити вправо, то в поперечному перерізі будуть діяти складові напружень і 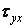, а в поздовжньому — і .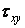

Зв'язок між складовими напружень у декартовій і полярній системах координат для плоскої задачі одержимо з відповідних формул, змінюючи в них позначення напрямків:

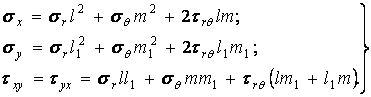
(а)

У цих формулах напрямні косинус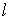и й 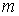визначають положення осі по відношенню відповідно до осей 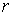і :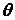

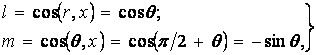
(б)

а напрямні косинус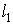и й 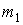- положення осі :

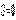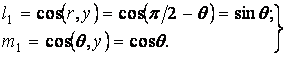
(в)

Після підстановки напрямних косинусів (б) і (в) у формули (а) одержуємо

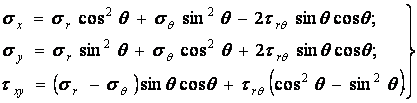
(4.13)

Користуючись значеннями напружень (4.13), знаходимо

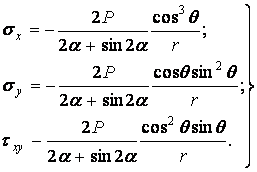
(г)

Перейдемо в правій частині отриманих рівностей від полярних координат до декартових, зв'язок між якими виражається в такий спосіб:

(4.14)

Підставляючи ці співвідношення у формули (г), одержуємо

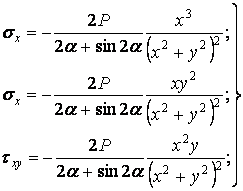
(4.15)

Досліджуємо виведені формули на прикладі клина з кутом 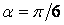рад. У перерезі 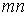, що перебуває на відстані 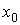від вершини,

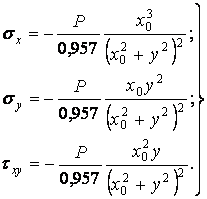
(д)

Епюри цих напружень зображені на рис. 4.5.

Для порівняння приведемо рішення з позицій опору матеріалів, де приймають, що при стисканні нормальні напруження в поперечному перерізі 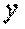розподілені рівномірно, а напруження й 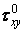відсутні:

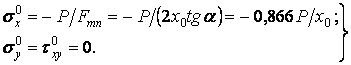
Зіставляючи ці напруження з напруженнями (д), містимо, що нормальне напруження 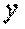, одержувана методами опору матеріалів, відрізняється від максимального нормального напруження , одержуваного методами теорії пружності, на 17%. У випадку, коли кут 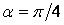рад, ця різниця досягає 36%. Звідси видно, що методика опору матеріалів непридатна для розрахунку стиснутих стержнів змінного перерізу з більшим кутом розтвору .

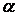Читайте також:

Згинання клина

<== попередня сторінка	\|	наступна сторінка ==>
Клин, навантажений у вершині зосередженою силою	\|	Згинання клина

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.