Згинання клина

Задача про згинання клина силою, прикладеною до його вершини (рис. 4.6), можна також розглядати як окремий випадок задачі, розібраної в 4.3, при .

Рис. 4.6. Вигин клина

Дотримуючись тої ж послідовності, що й у попередньому параграфі, знаходимо значення постійних:

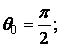
і складових напружень:

(4.16)

Епюра радіальних напружень у перерезі 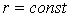показана на зазначеному рисунку.

Переходячи за допомогою формул (4.14) і (4.15) до декартової системи координат, знаходимо

(4.17)

Досліджуємо розподіл напружень у клині з кутом 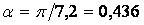рад. У цьому випадку в поперечному перерізі, що відстоїть від вершини на відстані 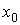, виникнуть наступні напруження:

Їх епюри також показані на рис. 4.6.

Для порівняння приведемо рішення, одержуване методами опору матеріалів:

(4.18)

Епюри цих напружень при тім же значенні кута 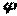представлені на рис. 4.7.

Рис. 4.7. Епюри, отримані методами опору матеріалів

Порівнюючи відповідні епюри на рис. 4.6 і 4.7, зауважуємо, що вони значно відрізняються друг від друга. Епюра нормальних напружень , побудована по формулах (4.17), криволінійна, а епюра напружень , побудована по формулах (4.18), прямолінійна, причому максимальні значення напружень відрізняються на 17%. Зі збільшенням кута 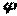ця різниця зростає.

Епюри дотичних напружень 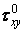і 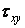взагалі не мають нічого загального. Нормальні напруження по всьому перерізу дорівнюють нулю, а максимальне значення нормального напруження для досліджуваного кута 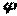становить близько 22% від максимального значення нормального напруження .

Зі зменшенням кута 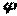розбіжність між рішеннями теорії пружності й опори матеріалів також зменшується. Отже, методика опору матеріалів придатна лише для малих кутів.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Стискання клина	\|	Дія зосередженої сили, прикладеної до границі напівплощини

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.01 сек.