• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Дія зосередженої сили, прикладеної до границі напівплощини

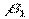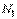На рис. 4.8 зображено пружне середовище, обмежене площиною і яка простягається необмежено донизу. В точці прикладена сила , перпендикулярна площини .

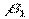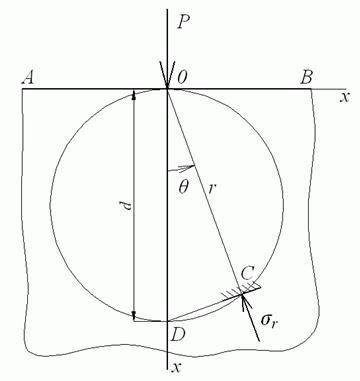
Рис. 4.8. Пружна напівплощина

У випадках плоскої задачі розглянуте середовище називається пружною напівплощиною. Таких випадків може представитися два. Якщо довжина середовища в напрямку, перпендикулярному площині креслення, досить мала, то виникає узагальнений плоский напружений стан. Якщо ж довжина середовища в зазначеному напрямку велика, то маємо справу із плоскою деформацією й у цьому випадку сила 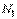являє собою навантаження, рівномірно розподілене уздовж прямій, перпендикулярній площині креслення.

Напівплощину можна розглядати як різновид клина при куті розтвору 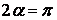. Думаючи також , тому що сила 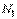спрямована уздовж осі , з формул (4.11) одержуємо постійні , .

Підставляючи ці значення у формули (4.12), знаходимо напруження в точках пружної напівплощини:

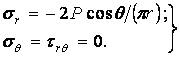
Французьким ученим Ж. Буссінеском запропоноване наступне графічне подання напруженого стану усередині напівплощини: якщо провести окружність, що касається границі напівплощини в точці додатка навантаження 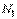, то ця окружність буде являти собою геометричне місце точок з однаковими радіальними напруженнями (коло Буссінеска). Доведемо це положення.

На рис. 4.8 окружність діаметром 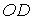, рівним , касається границі напівплощини 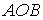в точці .Радіус-вектор, проведений у довільну точку 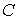, дорівнює 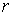. Із тригонометричних співвідношень у прямокутному трикутнику 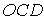треба, що , звідки . Використовуючи це співвідношення в першій формулі (4.19), одержуємо

(4.20)

Таким чином, у всіх точках зазначеної окружності радіальні напруження однакові.

Формули (4.19) можна застосовувати для визначення напружень на основі фундаменту. Хоча ґрунт основи найчастіше не має пружні властивості, при невеликих зовнішніх тисках практично для всіх ґрунтів можна приймати лінійну залежність між деформаціями й напруженнями і використовувати рівняння теорії пружності.

В інженерній практиці при розрахунку фундаментів необхідно знати розподіл напружень у товщі ґрунту по горизонтальному й вертикальному перерізах, тому в розглянутої задачі перейдемо від напружень у полярній системі координат до напружень у декартовій системі. Підставляючи значення напружень (4.19) у формули (4.13) одержуємо:

;

;

,

або, використовуючи формули переходу (4.14) від однієї системи координат до іншої,

(4.21)

Епюри нормальних і дотичних 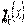напружень для двох горизонтальних перерезів показані на рис. 4.9, а, б. На рис. 4.9, в зображені епюри нормальних напружень для двох вертикальних перерізів. Нормальні напруги , що діють у горизонтальних перерізах, досягають максимуму під силою й загасають при видаленні від лінії її дії як завширшки, так і в глибину.

Дотичні напруження 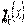під силою дорівнюють нулю, на деякій відстані від лінії її дії досягають максимуму, а потім поступово загасають. По мірі поглиблення максимум зміщується усе далі від осі . Так само як 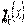, поводяться і нормальні напруження , що досягають максимального значення на тій же відстані, але по глибині.

а
б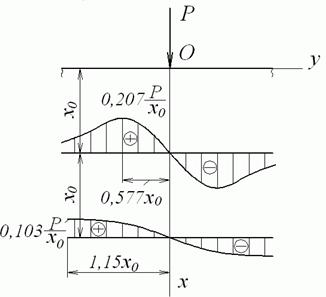
в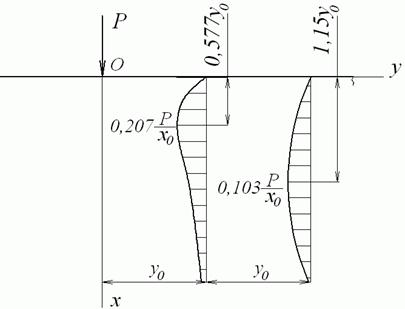

Рис. 4.9. Епюри напруг

Рішення для зосередженої сили можна поширити на випадок будь-якого суцільного розподіленого навантаження (рис. 4.10).

Рис. 4.10. Довільне розподілене навантаження

Якщо інтенсивність навантаження в даній точці дорівнює , то рівнодіюча навантаження на нескінченно малій довжині становить . Розмір у полярній системі координат має вигляд

.

Тут знак мінус з'являється тому, що при зростанні 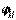кут 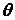убуває. Тоді елементарне навантаження на ділянці можна представити як

.

Вносячи це значення у формули (4.19), одержуємо напруження в точці від нескінченно малої сили , прикладеної в довільній точці на границі напівплощини:

; .

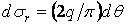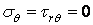За допомогою формул (4.13) переходимо до напружень, що виникають від нескінченно малої сили на горизонтальних і вертикальних площадках, що проходять через ту ж точку :

;

;

.

Якщо навантаження розподілене уздовж осі 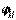від точки 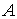до точки і кут 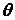змінюється в цих границях від 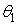, до 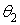, то, підсумовуючи напруження від кожної елементарної сили, одержуємо напруження в точці від всього розподіленого навантаження:

(4.22)

Щоб проінтегрувати вираз (4.22), навантаження необхідно представити у вигляді функції кута 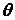. У випадку рівномірно розподіленого навантаження інтегрування значно полегшується, тому що 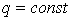. В результаті одержуємо

(4.23)

Читайте також:

1. Визначення границі витривалості. Діаграма утоми
2. Визначні границі
3. Границі й заливання осередків
4. Границя функції. Означення границі функції за Гейне й за Коші.
5. Де задана величина границі допустимого відхилення компетентності експерта з номером від максимальної.
6. Етап - визначають конкурентні сили, що діють у галузі, та оцінюють їх вплив на ситуацію у галузі.
7. Закони динаміки. Поняття маси, сили, імпульсу, імпульсу сили. Інерціальні системи відліку
8. Застосування фізичної сили, спеціальних засобів та зброї посадовими особами митної служби України.
9. Застосування фізичної сили, спеціальних засобів та зброї посадовими особами митної служби України.
10. ЛЕКЦІЯ 11. КОНТРОЛЬ І РЕВІЗІЯ ВИКОРИСТАННЯ РОБОЧОЇ СИЛИ, ФОНДУ ОПЛАТИ ПРАЦІ ТА РОЗРАХУНКІВ З РОБІТНИКАМИ І СЛУЖБОВЦЯМИ
11. Однобічні границі монотонної функції

Переглядів: 687