• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Клин, навантажений у вершині зосередженою силою

Рішення (4.7) можна застосувати до задачі про клин, у вершині якого прикладена сила 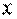довільного напрямку (рис. 4.3). Кут розтвору клина дорівнює 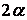. Початковий радіус-вектор 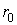збігається з бісектрисою кута. Лінія дії сили становить із початковим радіус-вектором кут .

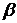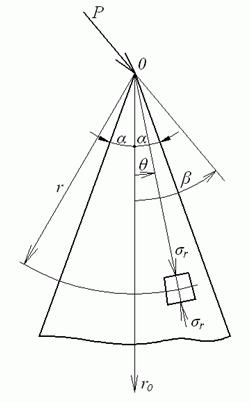
Рис. 4.3. До задачі про клин

Покажемо, що в цьому випадку клин перебуває в простому радіальному напруженому стані. Для цього скористаємося виразом напруження 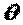у формі (4.6):

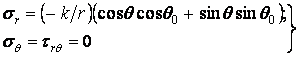
(4.8)

і визначимо постійні 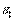й 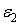, при яких задовольняються граничні умови поставленої задачі.

Виключимо з розгляду закріплення нижньої крайки клина, що впливає на розподіл напружень тільки поблизу від місця закріплення.

На бічних поверхнях клина, тобто при 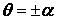, 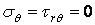. З формул (4.8) виходить, що ця умова тотожно виконується у всіх точках бічної поверхні, крім полюса 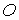. У полюсі при зазначені формули неприйнятні. Для включення в граничні умови сили 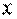замінимо її на підставі принципу Сен-Венана еквівалентним навантаженням, розподіленим по дузі малого радіуса 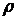(рис. 4.4).

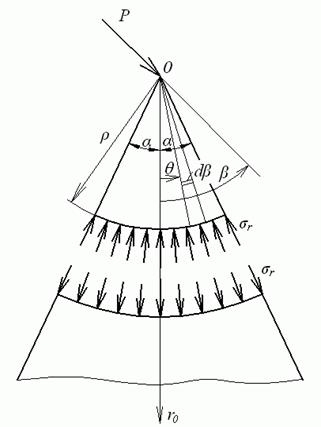
Рис. 4.4. Заміна зосередженої сили еквівалентним навантаженням

Розглянемо рівновагу елемента клина, що відсікається дугою довільного радіуса 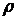. Спроектуємо всі сили, прикладені до цього елемента, на вертикальну і горизонтальну осі. Приймаючи товщину клина в напрямку, перпендикулярному площині малюнка, рівній одиниці, одержимо:

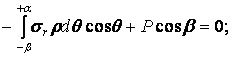
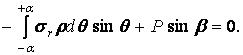
Після підстановки напруження 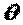з формул (4.8) при 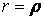ці умови рівноваги перетворяться в наступні:

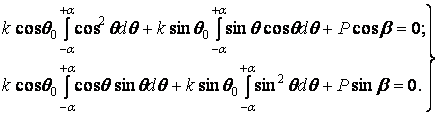
(а)

Інтегруючи, одержуємо систему двох рівнянь для визначення постійних 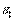і :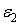

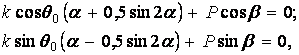
звідки

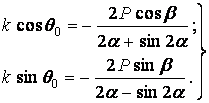
(б)

Розділивши почленно друге рівняння (б) на перше, одержуємо умову для визначення постійної :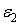

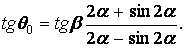
(4.9)

Зведемо обидва рівняння (б) у квадрат і складемо:

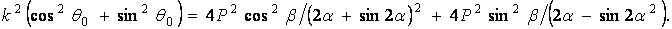
Добуваючи корінь, знаходимо

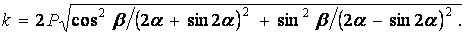
(4.10)

Таким чином, вдалося задовольнити граничним умовам і, отже, розглянутий клин перебуває в простому радіальному напруженому стані. При цьому постійні 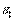й 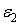визначаються формулами (4.9) і (4.10).

Читайте також:

1. Види джерел підприємницького права за юридичною силою
2. За юридичною силою
3. Згинання консолі силою, прикладеною на кінці
4. Зміст принципу незастосування сили чи погрози силою та особливості його прояву в міжнародному економічному праві
5. Класифікація електролітів за їх силою
6. Навантаження, поперечною силою і згинальним моментом
7. Навантаження, поперечною силою і згинальним моментом
8. Особливості магнітних кіл зі змінною магніторушійною силою
9. Постійний розвиток і вдосконалення виробництва – необхідна умова його існування, і саме проектування чи проектна технологія виступає рушійною силою його розвитку і вдосконалення.
10. Постійний розвиток і вдосконалення виробництва – необхідна умова його існування, і саме проектування чи проектна технологія виступає рушійною силою його розвитку і вдосконалення.
11. При цьому особовий склад пожежних підрозділів є головною та вирішальною силою у виконанні бойових задач по рятуванню людей у випадку загрози їх життю та гасінню пожеж.

Переглядів: 491