• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Навантаження, поперечною силою і згинальним моментом

Залежності між інтенсивністю розподіленого

Поперечна сила і згинальний момент

При дослідженні напружень, що виникають у балці при згині, будемо користуватися методом перерізів. Перерізаємо балку площиною перпендикулярною до її осі і розглядаємо рівновагу однієї частини, яка перебуває під дією зовнішніх навантажень і невідомих внутрішніх сил, певним чином розподілених по зробленому перерізі. Внутрішні сили повинні зрівноважувати всі зовнішні навантаження (включаючи реакції опор), що діють на відсічену частину балки.

Розглянемо балку на двох опорах, навантажену вертикальним навантаженням і парою сил М (рисунок 8.3, а). Припустимо, що балка розрізана на дві частини перерізом m-n, взятим на відстані х від лівої опори (рисунок 8.3, б). Із статики відомо, що система паралельних сил R_А

Рисунок 8.3

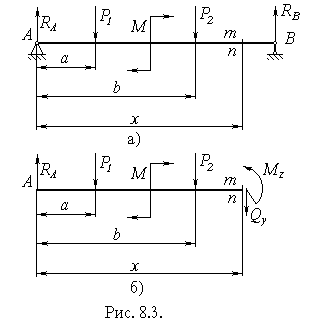
, Р1 , Р2 і пара сил М, які діють на ліву частину балки, можуть бути зведені до однієї вертикальної сили і пари сил. Отже, внутрішні сили, що діють в перерізі m-n, також можна звести до вертикальної рівнодійної і до пари сил. Позначимо величину рівнодійної внутрішніх сил через Qy , а момент внутрішніх сил відносно осі z, що проходить через центр ваги перерізу m-n і перпендикулярна до площини рисунка, через Mz . Сила Qy називається поперечною

силою , а момент M_z - згинальним моментом у довільному перерізі балки, взятому на відстані x від початку координат. Поперечна сила і згинальний момент є внутрішніми силовими факторами в поперечних перерізах балки при згині.

Для визначення величини поперечної сили запишемо рівняння рівноваги для всіх сил, які діють на ліву частину балки

,

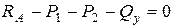звідки

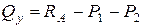. (8.1)

Для визначення величини згинального моменту, складемо рівняння моментів усіх сил, що діють на ліву частину балки, відносно осі z, яка проходить через центр перерізу m-n

,

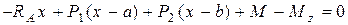звідки

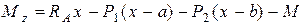. (8.2)

Поперечна сила і згинальний момент, знайдені з розгляду рівноваги правої частини балки, будуть мати ті самі значення, але напрямок їх буде протилежним. Це випливає з того, що всі сили, включаючи реакції, є системою сил, що перебувають у рівновазі.

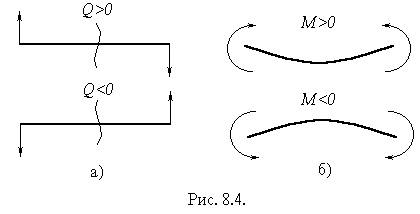
Для того, щоб поперечна сила і згинальний момент, визначені з розгляду лівої та правої частин балки, були однакових знаків, слід дотримуватися певного правила знаків.

Рисунок 8.4

Поперечну силу будемо вважати додатною, якщо вона намагається повернути вирізаний елемент за стрілкою годинника (рисунок 8.4, а). Згинальний момент будемо вважати додатним, якщо він вигинає балку опуклістю вниз (стиснуті верхні волокна) (рисунок 8.4, б).

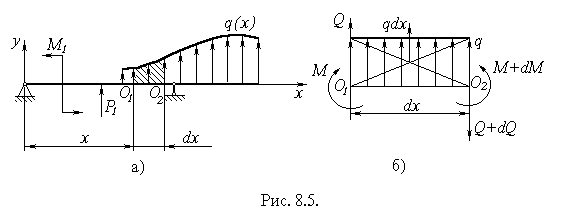
Установимо залежність між інтенсивністю розподіленого навантаження, поперечною силою і згинальним моментом. Для цього розглянемо балку навантажену довільним навантаженням (рисунок 8.5, а). Виріжимо елемент балки завдовжки dx (рисунок 8.5, б). Протягом довжини dx навантаження q вважатимемо розподіленим рівномірно.

Рисунок 8.5

Складемо рівняння рівноваги виділеного елемента балки. Сума проекцій всіх сил на вісь y

,

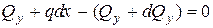звідки

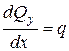. (8.3)

Складемо рівняння моментів всіх сил відносно осі z, яка проходить через точку О

.

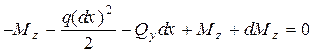Відкидаючи 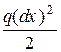як нескінченно малу величину другого порядку, отримаємо

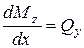. (8.4)

Із двох отриманих диференціальних залежностей (8.3) і (8.4) легко отримати третю

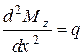. (8.5)

Читайте також:

1. За юридичною силою
2. Навантаження, поперечною силою і згинальним моментом
3. Особливості магнітних кіл зі змінною магніторушійною силою
4. Позначимо через ЕРС еквівалентного джерела, через –еквівалентний опір навантаження, через – внутрішній еквівалентний опір джерела енергії. Тоді матимемо
5. Постійний розвиток і вдосконалення виробництва – необхідна умова його існування, і саме проектування чи проектна технологія виступає рушійною силою його розвитку і вдосконалення.
6. При цьому особовий склад пожежних підрозділів є головною та вирішальною силою у виконанні бойових задач по рятуванню людей у випадку загрози їх життю та гасінню пожеж.
7. Розрахунок магнітних кіл з постійною магніторушійною силою
8. Чим напруженіше розумове навантаження, тим більше у корі головного мозку утворюється міжнейронних контактів!
9. Які напруження виникають при одночасному навантаженні бруса осьовою силою та згинаючим моментом?

Переглядів: 1578