• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Епюри поперечних сил і згинальних моментів

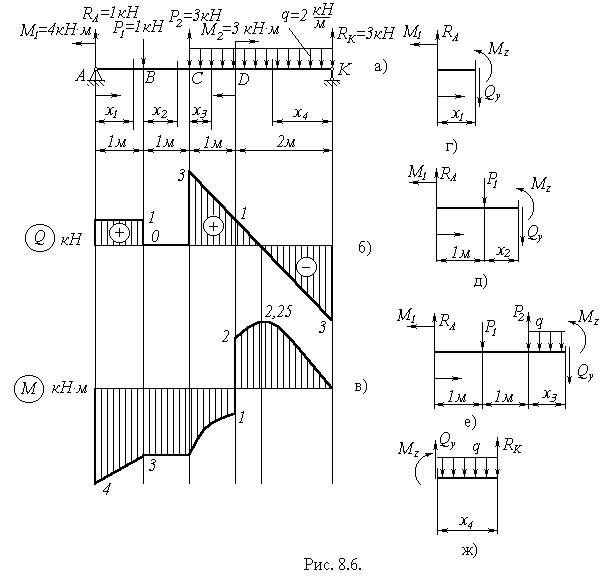
Поперечна сила і згинальний момент, будучи функціями від абсциси х, змінюються по довжині балки. Для визначення найбільш небезпечних перерізів балки зміну поперечної сили і згинального моменту по довжині балки зручно зображувати графічно. Такі графіки мають назву епюр поперечних сил і згинальних моментів. Розглянемо на прикладі порядок побудови епюр для балки.

Побудуємо епюри поперечних сил і згинальних моментів для балки, показаної на рисунку 8.6, а.

Спочатку визначимо реакції опор R_A i R_K .

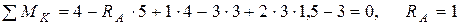кН,

кН.

Перевірка:

.

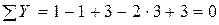Отже, реакції розраховано правильно.

Побудуємо епюри Q_y i M_z для ділянки АВ. Для цього зробимо переріз m₁-n₁ на відстані х від опори А і розглянемо рівновагу відсіченої частини (рисунок 8.6, г). Згинальний момент M_z і поперечну силу Q_y в перерізі будемо зображати додатними, хоч це не обов’язково .

Ділянка АВ

0 £ x₁ £ 1 м

Q_y=R_A=1 кН (8.6)

M_z=R_Ax₁-M₁ (8.7)

при x₁=0 м M_z=-4 кН×м,

при x₁=1 м M_z=-3 кН×м.

Рисунок 8.6

Як видно із (8.6) і (8.7) поперечна сила залишається сталою на всій довжині ділянки АВ а згинальний момент змінюється за лінійним законом. Графіки цих залежностей показані на рисунку 8.6, б і рисунку 8.6, в. Додатні значення сили Q_y будемо відкладати вгору від базової прямої, а від’ємні - вниз. Епюри згинальних моментів домовимося будувати на стиснутих волокнах. Тому вгору від базової лінії будемо відкладати в масштабі додатні значення згинального моменту, а вниз - від’ємні.

Побудуємо епюри М_z i Q_y для ділянки ВС. Для цього зробимо переріз

m₂-n₂ і розглянемо рівновагу лівої відрізаної частини балки (рис. 8.6, д)

Ділянка ВС

0 £ x₂ £ 1 м

Q_y=R_A-P₁=1-1=0 кН (8.8)

M_z=R_A(1+x₂)-P₁x₂ -M₁ (8.9)

при x₂=0 м M_z=-3 кН×м,

при x₂=1 м M_z=-3 кН×м.

Будуємо графіки функцій (8.8) і (8.9) на ділянці ВС (риc. 8.6, б, в).

Із умов рівноваги лівої відсіченої частини балки знаходимо закони, за якими змінюються Q_y i M_z на ділянці CD.

Ділянка CD

0 £ x₃ £ 1 м

Q_y=R_A-P₁+P₂-qx₃ (8.10)

при x₃=0 м Q_y =3 кН,

при x₃=1 м Q_y =1 кН,

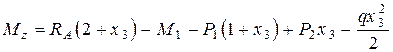(8.11)

при x₃=0 м M_z=-3 кН×м,

при x₃=1 м M_z=-1,75 кН×м.

Для побудови епюр Q_y i M_z на ділянці DK розглянемо рівновагу правої відрізаної частини балки (переріз m₃-n₃ , рисунок 8.6, е)

Ділянка DK

0 £ x₄ £ 2 м

Q_y=qx₄-R_K (8.12)

при x₄=0 м Q_y =-3 кН,

при x₄=2 м Q_y =1 кН,

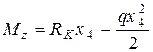(8.13)

при x₄=0 м M_z=0 кН×м,

при x₄=2 м M_z=2 кН×м.

Із (8.4) випливає, що при Q_y =0 момент M_z приймає екстремальне зна

чення. Значення х₁, при якому Q_y =0, знайдемо з рівняння (8.12)

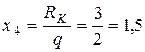м

Визначимо величину згинального моменту за формулою (8.13),при х₄=1,5 м

M_z=2,25 кН×м

Будуємо епюри Q_y i M_z на ділянці DK (рис. 8.6, б, в).

Як видно із рисунків 8.6, б, в на ділянках, де немає розподіленого навантаження (q=0), поперечна сила Q_y залишається сталою, а момент M_z змінюється за лінійним законом (ділянка АВ). На ділянці ВС Q_y=0, а M_z=const. На ділянці з рівномірно розподіленим навантаженням (q=const), епюра Q_y - лінійна, а згинальний момент M_z змінюється за законом квадратичної параболи (ділянка CD).

В перерізах, де прикладені зосереджені сили, на епюрі Q_y мають місце стрибки на величину і в напрямках цих сил, а на епюрі M_z - злами.

В перерізах, де прикладені зосереджені моменти, на епюрі Q_y ніяких змін немає, а на епюрі M_z мають місце стрибки на величину цих моментів.

На ділянках, де Q_y=0, момент M_z сталий, а в перерізах, де Q_y=0, згинальний момент набуває екстремального значення. Практично всі наведені властивості епюр Q_y i M_z випливають із залежностей (8.3) і (8.4).

Читайте також:

1. Аналітичний вираз сил і моментів.
2. Безрозмірною характеристикою гідротрансформатора називається залежність коефіцієнтів пропорційності моментів насосного і турбінного коліс від його передаточного відношення.
3. Вимірювання крутних моментів
4. Вимірювання сил і крутячих моментів
5. Властивості вибіркових моментів
6. Епюри Q та M при зміні
7. Епюри гідростатичного тиску.
8. Епюри крутних моментів
9. З.1 Ремонт повздовжніх та поперечних направляючих каретки супорту.
10. З.1 Ремонт повздовжніх та поперечних направляючих каретки супорту.
11. Метод моментів

Переглядів: 5533