• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Парамагнетизм Паулі

Функція розподілу Фермі-Дірака

,

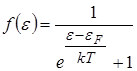дає імовірність того, що у стані теплової рівноваги ідеального електронного газу при температурі 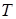стан з енергією 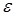зайнятий електроном, а енергія 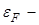має назву енергія Фермі і визначається як енергія електронів на найвищому за енергією ще заповненому рівні.

Рівняння Шрьодінгера для вільної частинки (у нашому випадку – вільні електрони) у тривимірному випадку має вигляд

,

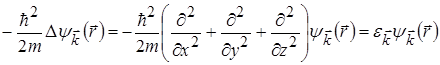де 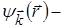хвильова функція, квадрат якої дає імовірність знаходження частинки у певному стані, 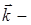хвильовий вектор (вектор, напрямок якого співпадає із напрямком розповсюдження хвилі, а чисельно він дорівнює хвильовому числу , 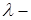довжина хвилі), потенціальна енергія у операторі Гамільтона відсутня, оскільки розглядаємо ідеальний електронний газ. Якщо електрони знаходяться у обмеженому об’ємі у вигляді кубу зі стороною 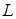, розв’язок цього рівняння будемо шукати у вигляді біжучої пласкої хвилі

за умови, що компоненти хвильового вектора 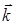набувають значень

,

і аналогічні набори для 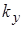і . Тобто кожна компонента хвильового вектора має вигляд , де 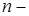довільне ціле (додатнє або від’ємне) число. Підставивши рівняння хвилі у рівняння Шрьодінгера, отримаємо вираз значень енергії електронів із хвильовим вектором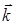

.

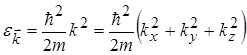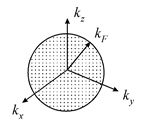
У основному стані систему із вільних електронів можна описувати точками всередині всередині сфери у просторі. Енергія, що відповідає поверхні цієї сфери, є енергією Фермі

,

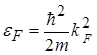а сама поверхня називається поверхнею Фермі (у даному випадку це сфера).

Радіус сфери Фермі можна знайти із наступних міркувань. Із умов, накладених на компоненти хвильового вектора, випливає, що кожному дозволеному хвильовому вектору відповідає у просторі елемент об’єму об’ємом . Тому у сфері Фермі об’ємом 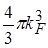кількість точок, що відповідає дозволеним станам електронів, дорівнює кількості комірок об’ємом . Отже, кількість дозволених станів для електронів є відношенням об’єму сфери Фермі до розміру комірки

,

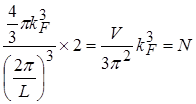яке згідно із принципом Паулі треба помножити на 2 (у певному енергетичному стані можуть бути тільки 2 електрони із протилежно направленими спінами). У стані рівноваги всі дозволені стани будуть зайняті електронами, отже кількість станів дорівнює кількості електронів. Звідси ми можемо знайти радіус сфери Фермі

,

де 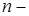концентрація електронів. Зауважимо, що радіус сфери Фермі визначається лише концентрацією електронів, але не залежить від маси.

Підставивши радіус сфери Фермі у вираз для енергії Фермі, маємо зв’язок енергії Фермі з концентрацією і масою електронів

.

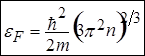Із співвідношення 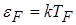вводять так звану температуру Фермі

,

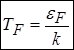яка ніяким чином не пов’язана із температурою електронного газу !

Енергетичні стани електронів розподілені по енергіях нерівномірно, тому користуються поняттям кількості станів на одиничний енергетичний інтервал, яку ще називають густиною станів . Знайдемо повну кількість станів із виразу для енергії Фермі

.

Тоді густина станів з енергією Фермі

.

Тепер повернемось власне до нашої задачі про парамагнетизм. Вектор намагнічування визначається як

,

де 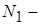концентрація електронів з магнітним моментом, паралельним магнітному полю, а концентрація електронів з магнітним моментом, антипаралельним магнітному полю.

Магнітне поле викликає розщеплення енергетичних рівнів. Тоді кількість електронів із паралельним магнітним моментом, що попадає у одиничний енергетичний інтервал,

,

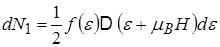де множник виник тому, що зсув енергетичних рівнів при розщепленні невеликий, і кількість електронів із паралельним і антипаралельним розташуванням магнітного моменту відносно магнітного поля приблизно однакова. До виразу входить густина енергетичних станів, де враховано зсув по енергіях до низу, імовірність заповнення станів та енергетичний проміжок . Аналогічно для кількості електронів із антипаралельним магнітним моментом, що попадає у одиничний енергетичний інтервал,

.

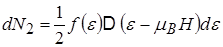Повну кількість всіх електронів знайдемо інтегруванням, причому треба врахувати, що верхнею межею енергії є рівень Фермі, він однаковий для обох типів електронів, а нижні межі інтегрування будуть різними :

;

.

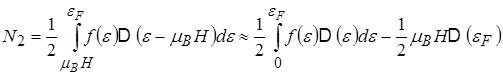Розіб’мо інтеграли кожен на два, і після очевидних перетворень отримаємо відповідні співвідношення.

Тепер переходимо до вектора намагніченості. Підставивши у нього вирази для концентрацій, маємо

.

Виразимо кустину станів через концентрацію, а енергію Ферми через температуру Фермі, тоді

.

Остаточно отримаємо вираз для паулівської спінової намагніченості електронів

,

звідки магнітна сприйнятливість

.

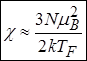Зверніть увагу, магнітна сприйнятливість електронного газу вже не залежить від температури.

Переходимо до наступного різновиду магнетиків – феромагнетиків.

Читайте також:

1. Діа- і парамагнетизм.
2. Принцип Паулі. Стани електронів у складних атомах

Переглядів: 822