• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Обчислення суми ряду

Завдання зводиться до знаходження суми

S=u(l) + u(2) +... + u(n)+...= ,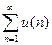

кожен доданок якої є функцією від номера n, що визначає місце цього доданка в сумі, а також може бути функцією одного або декількох додаткових параметрів, наприклад

або

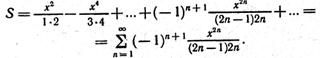
Обчислення суми ряду складається в одержанні в результаті циклічного процесу послідовності s(1), s(2), ..., s(n), ..., що сходиться до свого граничного значення, тобто межі . Тут s(n) - сума n членів нескінченного ряду.

В загальному випадку початкове значення номера члена ряду n може бути відмінним від 1 (наприклад, рівним 0). Позначивши його через v, одержимо

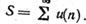(5.9)

Для обчислення суми ряду використається розглянутий вище прийом нагромадження суми: підсумовування вважається закінченим при виконанні умови досягнення заданої погрішності 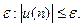. Завдання знаходження суми ряду являє типовий приклад ітераційного процесу, тому що заздалегідь не відомо, при якому числі членів ряду буде досягнута необхідна точність.

Процес обчислень визначається рекуррентним співвідношенням s(n) = s(n - 1) + u(n). Для визначення початкового значення суми перепишемо (5.9) у вигляді

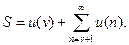
Елемент u(v) можна прийняти як початкове значення суми, а параметр n в ітераційному процесі буде приймати значення v+1, v+2, ....

Загальна схема алгоритму обчислення суми членів нескінченного ряду наведена на мал. 5.11. Оскільки в обчисленнях по рекуррентной формулі одночасно беруть участь лише два значення s(n) і s(n - 1), у схемі алгоритму замість цих змінних використається змінна S (блок 3). Значення S буде змінюватися щораз при додатку чергового члена суми. Праворуч від знака присвоювання значення змінної відповідає попередньому значенню суми s(n - 1), ліворуч - поточний s(n).

Звичайно формула загального члена суми належить одному з наступних типів:

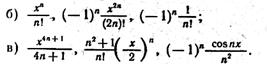
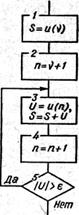
Рис. 5.11

У випадку а) обчислення будуть найбільш ефективними, якщо кожен член суми u(n) (мал. 5.11, блок 3) обчислювати по загальній формулі.

У випадку б) у формулу члена суми й u(n) входять цілі ступені й факторіали, для обчислення й u(n) доцільно використати рекуррентні співвідношення, тобто виражати наступний член суми через попередній. Це дозволить істотно скоротити обсяг обчислень. Крім того, безпосереднє обчислення члена суми по загальній формулі в ряді випадків, неможливо, наприклад через наявність n! або при х 0. Черговий член ряду й u(n) можна визначити через попередній у такий спосіб:

u(n) = u(n -1 )?(n), де ?(n) - перехідний коефіцієнт, що залежить від n.

Наприклад, при обчисленні суми .

перехідний коефіцієнт можна визначити в такий спосіб:

Як початкове значення, члена ряду вибирається значення u(v) (для наведеного приклада v = 0).

Для випадку б) схема алгоритму обчислення суми нескінченного ряду наведена на мал. 5.12.

У випадку в) член суми доцільно представити у вигляді двох співмножників:

u(n) =з(n)а(n),

один із яких обчислюється по рекуррентному співвідношенню, а інший безпосередньо. Схема алгоритму для випадку в) наведена на мал. 5.13. Наприклад, якщо й 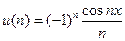, те думаємо з(n)=(—1)ⁿ й обчислюємо рекуррентно

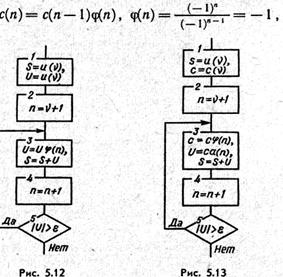
де початкове значення параметра з дорівнює c(v). Для даного приклада v=l, u(v) = — cos x, c(v) = —1. Співмножник 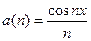- зручно обчислювати безпосередньо по формулі.

Розглянемо конкретний приклад. Нехай необхідно обчислити суму членів ряду

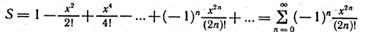
з точністю до члена ряду, меншого 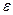, для заданого х.

Загальний член суми ставиться до типу б). Сума обчислюється за схемою на мал. 5.12. Визначимо коефіцієнт переходу від попередні (n- 1)-го члена ряду до чергового що обчислює n-му:

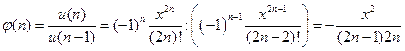
Початкове значення: v = 0, u(v)=l. Схема алгоритму рішення завдання наведена на мал. 5.14. Програма має такий вид:

10 INPUT X, Е

20 LET S= 1:LET U= 1

30 LET N = 1

40 LET U=-U*X*X/((2*N-1)*2*N)

50 LET S = S + U

60 LET N = N+1

70 IF ABS (U)>E THEN 40

80 PRINT "N = "N, "S = "S

90 END

Тут ітераційний циклічний процес реалізований за допомогою умовного логічного оператора. Якщо в результаті помилки перехідний коефіцієнт 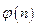буде обчислений невірно, то при виконанні такої програми може відбутися зациклення. Програмування ітераційного циклу за допомогою оператора циклу FOR дозволяє уникнути цього. Як максимальне значення параметра циклу в цьому випадку потрібно вибрати значення, «гарантуюче» досягнення заданої точності обчислень (значення, при якому n-й член ряду u(n) свідомо менше 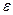). Схема алгоритму рішення завдання з використанням блоку модифікації наведена на мал. 5.15. Для даного приклада максимальне значення n можна прийняти рівним 20. Тоді програма буде мати такий вигляд:

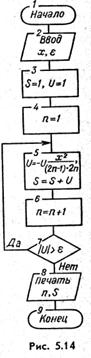
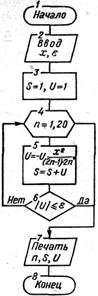
10 INPUT X, E

20 LET S= 1:LET U=l

30 FOR N = 1 TO 20

40 LET U = -U*X*X/((2*N-1)*2*N)

50 LET S=S + U

60 IF ABS (U)<=E THEN 80

70 NEXT N

80 PRINT "N = "N, "S = "S,"U = "U

90 END

Тут значення останнього члена ряду й число повторень циклу виводяться на печатку трива-контролю збіжності ітераційного процесу.

Читайте також:

1. Автододавання та автообчислення.
2. Алг W2 (ОБЧИСЛЕННЯ Y)
3. Аналітичні показники динаміки та прийоми їх обчислення
4. База оподаткування, ставки податку та порядок обчислення.
5. Безпосереднє обчислення з використанням формули Ньютона-Лейбніца.
6. Валовий національний продукт і його обчислення
7. Види середніх і способи їх обчислення
8. Визначення та обчислення функції для одного значення аргументу і для діапазону значень аргументу.
9. Відносні величини: суть, види та способи їх обчислення
10. Відносні величини: суть, види та способи їх обчислення
11. Відомість обчислення координат точок полігону
12. Відомість обчислення площі ділянки за координатами

Переглядів: 6183