Основні напрямки застосування СШІ в управлінні організацією

Функціональна підсистема менеджменту	Управлінські задачі	Модель СШІ
Стратегічне управління	Розроблення довгострокових прогнозів на багатоваріантній і багатосценарній основі.	Нейронні мережі Динамічні структурні моделі
Управління продажами	Профілювання покупця. Сегментація ринку. Визначення цін на продукцію. Прогнозування попиту і продажів. Розрахунок рекламного бюджету.	Нейронні мережі Нечіткі множини
Управління закупівлями	Передбачення ринкових цін і макроекономічних показників. Управління запасами. Оптимізація графіка закупівель. Транспортна задача.	Генетичні алгоритми Нечіткі множини Динамічні структурні моделі
Управління виробництвом	Управління товарно-матеріальними потоками. Визначення оптимального товарного портфеля. Складання графіка робіт.	Генетичні алгоритми Динамічні структурні моделі
Управління якістю	Оцінка показників якості. Управління якістю.	Нейронні мережі Нечіткі множини
Управління фінансами	Управління фінансовими потоками. Оцінка кредитоспроможності. Передбачення банкрутств. Рейтингування партнерів, конкурентів.	Нейронні мережі Динамічні структурні моделі
Управління персоналом	Управління людськими ресурсами. Оптимальне розміщення персоналу.	Генетичні алгоритми Динамічні структурні моделі

Штучні нейронні мережі (аrtificial neural networks) – математичні моделі, а також їх програмна та апаратна реалізація, побудовані за принципом функціонування біологічних нейронних мереж – мереж нервових клітин живого організму.

Нейронні мережі відносяться до класу нелінійних адаптивних систем з архітектурою, що умовно імітує нервову тканину з нейронів. Математична модель нейрона являє собою деякий універсальний нелінійний елемент із можливістю широкої зміни і налаштування його характеристик.

Штучний j-й нейрон задається сукупністю своїх входів (дендрити) – х_ij, ваговими коефіцієнтами входів (синапси) – w_ij, функцією стану (сома) – s_j та функцією активації (аксони) – f_j ().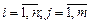

Функція стану s_j визначає стан нейрона залежно від його входів та ваг входів (рідше – ще й залежно від попередніх станів нейрона):

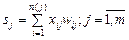де n(j) – кількість входів j-го нейрона.

Функцією стану s_j задається деяке порогове значення 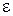. Якщо s_j > 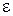, вихідний сигнал нейрона y_j = 1, в іншому випадку у_j = 0. Таким чином, нейрон може перебувати лише у двох станах: активному (коли вихідний сигнал y_j = 1) або пасивному (у_j = 0).

Функція активації y = f(s) визначає вихідний сигнал нейрона як функцію його стану s. Найбільш поширеними функціями активації є ступенева та лінійна порогові, сигмоїдна, лінійна і гаусівська. Лінійні нейромережі застосовують нейрони з лінійною функцією активації. Нелінійні застосовують нелінійну функцію активації, наприклад, порогову або сигмоїдну.

Узагальнену структурну схему j-го нейрона показано на рис. 10.1.

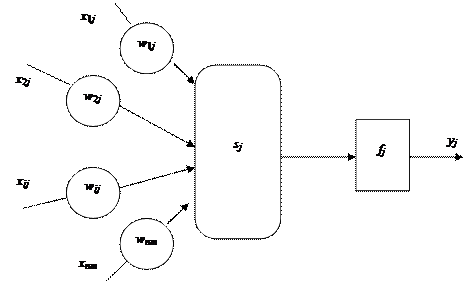
Рис. 10.1. Загальна структурна схема j-го нейрона

В одній з найбільш розповсюджених нейромережевих архитектур - багатошаровому персептроні зі зворотним поширенням похибки - моделюється робота нейронів у складі ієрархічної мережі, де кожен нейрон прошарку з'єднаний своїми виходами з входами нейронів наступного прошарку (рис. 10.2). На нейрони вхідного прошарку подаються значення вхідних параметрів, на основі яких виробляються обчислення, необхідні для прийняття рішень, прогнозування розвитку ситуації і т.п. Ці значення розглядаються як сигнали, що передаються в наступний прошарок. Величина послаблення або підсилення сигналу залежить від числових значень (ваг), приписуваних міжнейронним зв'язкам. У результаті цього на виході нейрона вихідного прошарку продукується значення, що розглядається як відповідь, реакція всієї мережі на введені значення вхідних параметрів. Для того щоб мережу можна було застосовувати надалі, її треба "навчити" на прикладах, для яких відомо і значення вхідних параметрів, і правильні відповіді на них.

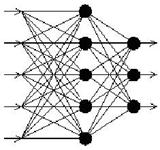
Рис. 10.2. Багатошаровий персептрон

Процес "навчання" полягає в підборі ваг міжнейронних зв'язків і модифікації внутрішніх параметрів передатної функції нейронів. Для кожного сполучення навчальних даних на виході мережі вихідні значення порівнюються з відомим результатом. Якщо вони розрізняються, то обчислюється похибка, що враховується при обробці у вузлах мережі. Зазначені кроки повторюються, поки не виконається умова останову, наприклад необхідна похибка не буде перевищувати заданої величини.

Отже, нейронні мережі уявляють собою сукупність зв'язаних між собою вузлів, що отримують вхідні дані, здійснюють їх обробку і генерують на виході результат. Між вузлами видимих вхідного і вихідного прошарків може знаходитися певне число прихованих прошарків обробки. Нейронні мережі реалізують непрозорий процес. Це означає, що побудована модель, як правило, не має чіткої інтерпретації. Багато пакетів, що реалізують алгоритми нейронних мереж, застосовуються не лише в сфері обробки комерційної інформації, без них важко обійтися при рішенні більш загальних задач розпізнавання образів, скажемо розшифровки рукописного тексту чи інтерпретації кардіограм.

Апаратні або програмні реалізації алгоритмів нейромереж називаються нейрокомп'ютером.

· Нейрокомп'ютери дають стандартний спосіб рішення багатьох нестандартних задач. І неважливо, що спеціалізована машина краще вирішує один клас задач. Важливіше, що один нейрокомп'ютер вирішить і цю задачу, і другу, і третю і не треба щораз проектувати спеціалізовану ЕОМ, нейрокомп'ютер зробить все сам і майже не гірше.

· Замість програмування навчання. Нейрокомп'ютер вчиться, потрібно лише формувати навчальні множини. Праця програміста заміняється новою працею вчителя. Краще це чи гірше? Ні те, ні інше. Програміст наказує машині всі деталі роботи, вчитель створює "навчальне середовище", до якого пристосовується нейрокомп'ютер. З'являються нові можливості для роботи.

· Нейрокомп'ютери ефективні там, де потрібний аналог людської інтуїції, зокрема, для розпізнавання образів, читання рукописних текстів, підготовки аналітичних прогнозів, перекладу з однієї природної мови на іншу і т.п. Саме для таких задач звичайно важко скласти явний алгоритм.

· Нейронні мережі дозволяють створити ефективне програмне та математичне забезпечення для комп'ютерів з високим ступенем розпаралелювання обробки.

· Нейрокомп'ютери "демократичні", вони також дружні, як текстові процесори, тому з ними може працювати будь-який, навіть зовсім недосвідчений користувач.

Генетичний алгоритм (genetic algorithm) – це еволюційний алгоритм пошуку, що використовується для вирішення задач оптимізації і моделювання шляхом послідовного підбору, комбінування і варіації параметрів, що шукають, з використанням механізмів, які нагадують біологічну еволюцію.

Генетичні алгоритми є могутнім засобом рішення різноманітних комбінаторних задач і задач оптимізації. Проте, генетичні алгоритми ввійшли зараз у стандартний інструментарій методів інтелектуальних обчислень. Цей метод названий так тому, що в якомусь ступені імітує процес природного відбору в природі. Нехай нам треба знайти рішення задачі, найбільш оптимальне з погляду деякого критерію, де кожне рішення цілком описується певним набором чисел чи величин нечислової природи. Скажемо, якщо нам треба вибрати сукупність фіксованого числа параметрів ринку, найбільш виражено впливаючих на його динаміку, це буде набір імен цих параметрів. Про цей набір можна говорити як про сукупність хромосом, що визначають якості індивіда - даного рішення поставленої задачі. Значення параметрів, що визначають рішення, будуть тоді називатися генами. Пошук оптимального рішення при цьому схожий на еволюцію популяції індивідів, представлених їхніми наборами хромосом. У цій еволюції діють три механізми: по-перше, відбір найсильніших - наборів хромосом, яким відповідають найбільш оптимальні рішення; по-друге, схрещування - виробництво нових індивідів за допомогою змішування хромосомних наборів відібраних індивідів; і, по-третє, мутації - випадкові зміни генів у деяких індивідів популяції. У результаті зміни поколінь виробляється таке рішення поставленої задачі, що вже не може бути далі поліпшено.

Генетичні алгоритми мають два слабких місця. По-перше, сама постановка задачі в їхніх термінах не дає можливості проаналізувати статистичну значимість одержуваного з їх допомогою рішення і, по-друге, ефективно сформулювати задачу, визначити критерій відбору хромосом під силу тільки фахівцю. У силу цих факторів сьогодні генетичні алгоритми треба розглядати скоріше як інструмент наукового дослідження, ніж засіб аналізу даних для практичного застосування в бізнесі і фінансах.

Нечітка логіка і теорія нечітких множин – це розділ математики, що є узагальненням класичної логіки і теорії множин. Поняття нечіткої логіки було вперше введене професором Л. Заде в 1965 р. Ним поняття множини було розширено допущенням, що функція належності елемента до множини може приймати будь-які значення в інтервалі [0, 1], а не тільки 0 або 1. Такі множини були названі нечіткими. Також були запропоновані різні логічні операції над нечіткими множинами і запропоноване поняття лінгвістичної змінної, у якості значень якої виступають нечіткі множини.

Предметом нечіткої логіки є побудова моделей наближених міркувань людини і їх використання в комп'ютерних системах.

Нечітка логіка заснована на використанні таких оборотів природної мови, як "далеко", "близько", "високий", "низький" тощо. Діапазон її застосування дуже широкий - від побутових приладів до управління складними процесами. Разом із тим, для того, щоб використовувати теорію нечіткості на комп'ютерах, необхідні математичні перетворення, що дозволяють перейти від лінгвістичних змінних до їх числових аналогів в ЕОМ.

Використання нечіткої логіки найбільш математично адекватне для рішення проблеми оцінки ризиків в процесі управління ними. Використовуючи нечітку логіку для обробки недетермінованих даних, можна оперувати лінгвістичними змінними, які є більш природними для людського розуміння при описанні елементів економічних систем.

Динамічні системи структурного моделювання. Системну динаміку, яка спирається на теорію автоматичного регулювання, можна лише умовно віднести до групи інтелектуальних інформаційних технологій.

У типовій структурно-динамічній моделі шість основних параметрів, тобто шість взаємозалежних потоків. П'ять з них – це сировина, замовлення, кошти, обладнання і робоча сила, шостий – інформаційний – служить для зведення всіх їх у єдине ціле. "Поведінка" моделі в основному визначається її структурою. Сама модель являє собою сукупність підсилювачів, запізнень та інтегруючих ланок, які пов'язані між собою згаданими вище потоками. Виходячи з цієї структури, можна скласти рівняння динаміки поведінки системи й одержати кількісні оцінки процесів, пов'язаних з різними збурюваннями і управлінськими впливами. Як правило, найбільш складні моделі, що відповідають практичним запитам загального господарського керівництва, містять до трьох тисяч змінних.

Методика побудови і аналізу структурно-динамічної виробничо-господарської моделі включає такі шість етапів: на першому визначається конкретне виробничо-господарське питання, що підлягає аналізу методом динамічного моделювання; на другому – словесно формулюються основні залежності, шо характеризують структуру досліджуваної системи; на третьому – будується її структурна модель, складається система рівнянь; на четвертому – система моделюється на комп'ютері і результати моделювання порівнюються з експериментальними даними про її реальну поведінку; на п'ятому етапі постає питання про таку модифікацію моделі, що забезпечила б зразковий збіг її з поведінкою системи на наявному експериментальному матеріалі; нарешті, шостий – заключний – етап полягає у відшукуванні на моделі доцільних змін параметрів, що приводять до поліпшення її поведінки, і перекладі цих змін з мови моделі на мову реальної системи.

До переваг динамічних систем варто віднести врахування часового фактору в обчислювальних експериментах, можливість імітації найважливіших функцій менеджменту. Методологія структурного моделювання з одночасною візуалізацією досліджуваних процесів може призвести до породження нових уявлень про бізнес і шляхи вирішення проблем. Імітаційні моделі, які об’єктивно відображають реальність, дозволяють заощаджувати значні засоби на стадії реалізації проектів. Недолік цих систем полягає в необхідності тривалого процесу послідовного ускладнення моделей для того, щоб вони адекватно відображали досліджуваний об’єкт.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Порівняння людської і штучної компетентності	\|	Основні категорії, ключові поняття та визначення теми.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.