• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Застосування геометричних перетворень для побудови ліній другого порядку.

Спрощення рівняння лінії за допомогою повороту системи координат.

Спрощення рівняння лінії за допомогою паралельного перенесення системи координат.

План.

Спрощення рівняння лінії другого порядку за допомогою геометричних перетворень.

Лекція 21

1. Інший підхід при дослідженні загального рівняння лінії другого порядку, який ми розглядаємо у даній лекції і який відрізняється від запропонованого раніше варіанту вивчення властивостей ліній, полягає у тому, що при заміні системи координат іншою системою рівняння лінії змінюється. Виявляється, що при вдалому виборі нової системи координат рівняння лінії можна суттєво спростити та звести до канонічного виду. З цього моменту для вивчення властивостей лінії та її зображення можна скористатись відомою нам канонічною теорією ліній другого порядку, яка розглядалась в лекціях 12-14.

Розглянемо, як перетворюється рівняння лінії другого порядку, заданої рівнянням

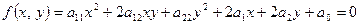, (1)

при паралельному перенесенні системи координат.

Нехай прямокутна декартова система координат одержана паралельним перенесенням системи 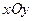у новий початок - точку 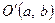. Розглянемо довільну точку площини, яка у початковій системі має координати , а в іншій прямокутній системі - координати 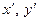. У лекції 6 ми отримали рівності

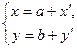, (2)

які визначають зв'язок між координатами точки у двох різних системах координат, одна із яких одержана паралельним перенесенням іншої.

Підставляючи одержані співвідношення у рівняння (1), отримуємо

,

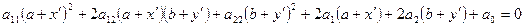або

. (3)

Аналізуючи рівняння (3), зробимо наступні висновки:

1) при паралельному перенесенні системи координат у новий початок коефіцієнти біля старших членів не змінюються;

2) вільний член у перетвореному рівнянні рівний ;

3) якщо лінія, задана рівнянням (1) – центральна точка 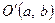є центром лінії, то у перетвореному рівнянні коефіцієнти біля та 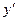будуть рівні нулю.

Останнє твердження випливає з того, що для центра лінії вирази та перетворюються в нуль.

Приклад 1. Побудувати лінію, задану рівнянням .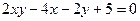

Розв’язання. Знайдемо центр лінії. Для цього розв’яжемо систему рівнянь 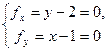. Оскільки 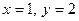, то початок нової системи координат потрібно вибрати у точці . Формули, за допомогою яких спрощується рівняння лінії, матимуть вигляд 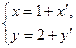. Обчисливши 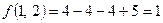та скориставшись розглянутими вище властивостями, дістаємо перетворене рівняння у виді 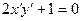або 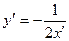. Побудова графіка одержаної залежності легко реалізується у системі координат (рис. 1). При цьому доцільно використати точки перетину лінії з осями початкової системи координат. На рисунку - це точки 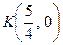та .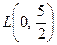

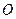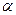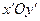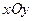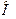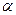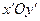2. Дослідимо, як перетворюється рівняння лінії при повороті системи координат навколо початку координат - точки на деякий кут . Нехай прямокутна декартова система координат одержана поворотом системи навколо точки на кут . Розглянемо довільну точку площини, яка в початковій системі має координати , а у новій системі - координати 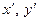(рис. 2) та нехай промінь утворює з віссю кут .

Оскільки , , 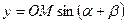, , 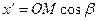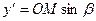то

,

.

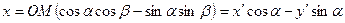Формули

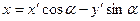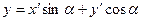, (4)

виражають зв’язок між старими та новими 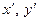координатами довільної точки площини. Вивчимо питання, чи можна, користуючись рівностями (4), спростити рівняння лінії (1)? Для цього, підставивши співвідношення (4) в (1), дістаємо

.

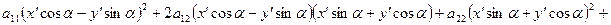
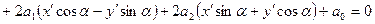Після очевидних перетворень одержане рівняння можна записати у виді

.

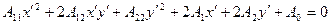Не обчислюючи всі коефіцієнти одержаного рівняння, зауважимо тільки, що

,

.

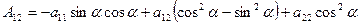Вважаючи, що кут повороту 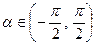, виберемо його так, щоб . Із рівняння

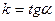після ділення його на та введення заміни дістаємо

. (5)

Із одержаним рівнянням ми уже зустрічались, вивчаючи питання існування головних напрямків лінії (1). Нагадаємо, що воно завжди має розв’язки, а корені даного рівняння дозволяють записати рівняння осей симетрії у виді , .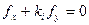

Зробимо наступні висновки:

1) при повороті системи координат на кут, при якому вісь приймає головний напрямок, коефіцієнт біля добутку 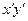в рівнянні лінії перетворюється в нуль;

2) вільний член у перетвореному рівнянні не змінюється.

Зауважимо також, що співвідношення 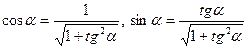дозволяють записати формули (4) перетворення координат при повороті системи у виді

, , (6) де - один із коренів рівняння (5).

Задача 2. Рівняння 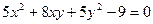звести до канонічного виду та назвати лінію, яка задається цим рівнянням.

Розв’язання. За допомогою повороту системи координат позбудемось доданка, який містить добуток змінних 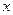та 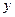. Для цього складемо та розв’яжемо рівняння виду (5):

, .

Із одержаних двох значень виберемо одне. Нехай 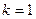. Тоді формули повороту (6) набувають виду , . Підставляючи їх у задане рівняння, дістаємо

,

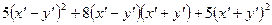звідки 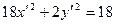, або .

Одержане канонічне рівняння показує, що задана лінія - еліпс.

3. Застосуємо перетворення паралельного перенесення та повороту до побудови ліній другого порядку, вважаючи, що вони задаються у виді (1).

Спочатку розглянемо випадок центральних ліній. Нехай точка 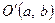- центр лінії (1), тобто її координати є розв’язком системи 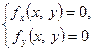. Тоді після паралельного перенесення системи 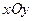у новий початок - точку 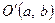в новій системі координат у перетвореному рівнянні коефіцієнти біля та 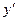будуть рівні нулю. Повертаючи одержану систему координат на кут 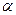, який визначається одним із коренів рівняння (5), отримаємо ще одну систему координат 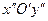. У цій системі рівняння лінії не міститиме як доданків із першими степенями змінних 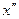та 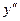, так і доданка з добутком . Побудова лінії за одержаним спрощеним рівнянням, яке можна записати у канонічному виді, здійснюється в системі 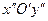. Зауважимо, що, оскільки згідно з формулами (2), (4), та 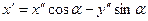, , 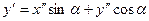то співвідношення

,

,

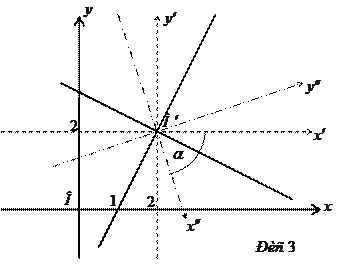
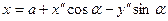які поєднують формули паралельного перенесення та повороту, дають можливість отримати спрощене рівняння безпосередньо із рівняння (1).

Задача 3. За допомогою геометричних перетворень спростити рівняння

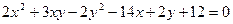
та побудувати лінію.

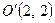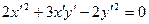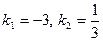Розв’язання. Склавши систему для відшукання центра та розв’язавши її, дістаємо початок нової системи координат, який знаходиться в точці . Обчисливши новий вільний член , записуємо рівняння лінії у системі координат . Воно матиме вид . Для знаходження кута повороту складаємо рівняння , звідки дістаємо . Нехай . Формули (6) запишуться у виді 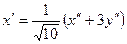, . Підставляючи їх у рівняння лінії та спрощуючи одержаний вираз, дістаємо рівняння . Очевидно, що побудова заданої лінії зводиться до побудови двох прямих у системі 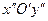, одержаній поворотом системи на кут 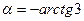(рис. 3).

У випадку, коли лінія, яка задана рівнянням (1), не має центра, як нам відомо з лекцій 19, 20, головний напрям визначається кутовим коефіцієнтом 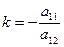. Оскільки спряжений напрям для осі симетрії параболи рівний 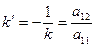, то її рівняння запишеться у виді 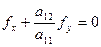. Якщо виконати паралельне перенесення системи координат у вершину параболи – точку 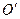, яку можна знайти, розв’язавши систему рівнянь 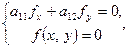то в одержаному рівнянні вільний член перетвориться в нуль. Це випливає з того, що парабола буде проходити через початок координат. Після повороту осі на кут 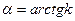у рівнянні пропаде доданок, який містить добуток 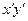, а вільний член не зміниться. Отримавши рівняння лінії у канонічному виді 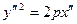, її можна побудувати у новій системі координат .

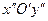Задача 4. Звести до канонічного виду рівняння та побудувати параболу.

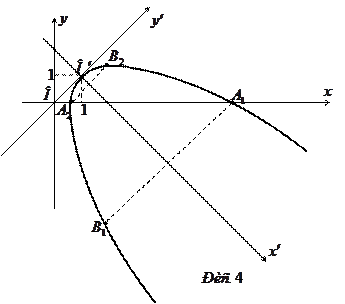Розв’язання. Знайдемо вершину параболи. Для цього розв’яжемо систему рівнянь 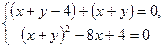. Дістаємо , звідки дістаємо координати нового початку координат 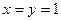. Виконавши паралельне перенесення у точку 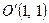, яке задається рівностями , дістаємо рівняння лінії у виді 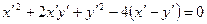. Оскільки 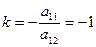, то кут повороту 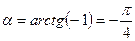. Формули повороту запишуться у виді

, ,

а після їхнього застосування рівняння лінії набуде виду . Зобразивши систему координат 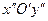та користуючись одержаним рівнянням, виконуємо побудову параболи (рис.4).

Зауважимо, що для більш точної побудови можна знайти деякі допоміжні точки на параболі, наприклад, точки її перетину з координатними осями. У нашому випадку при 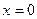дістаємо рівняння 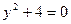, яке не має розв’язків, а при - рівняння із коренями 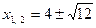, які визначають точки перетину параболи з віссю . При виконанні зображення використано також точки та , які розташовані симетрично до точок 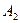та 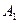відносно осі .

Читайте також:

1. DIMCLRE (РЗМЦВЛ) - колір виносних ліній (номер кольору). Може приймати значенняBYBLOCK (ПОБЛОКУ) і BYLAYER (ПОСЛОЮ).
2. II. Критерій найбільших лінійних деформацій
3. V. Виконання вправ на застосування узагальнювальних правил.
4. А. Це наявність в однієї людини кількох ліній клітин з різним набором хромосом.
5. А.1 Стан , та проблемні питання застосування симетричної та асиметричної криптографії.
6. Автомобільні ваги із застосуванням цифрових датчиків
7. Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
8. Акти застосування норм права в механізмі правового регулювання.
9. Акти застосування юридичних норм: поняття, ознаки, види.
10. Акти правозастосування, їх види
11. Акти правозастосування.
12. Активний опір ліній електропередачі

Переглядів: 2720