• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Відношення еквівалентності та порядку, їх властивості. Впорядковані множини. Зв'язок відношення еквівалентності з розбиттям множини на класи, що попарно не перетинаються.

Бінарні відношення між елементами однієї множини, способи їхнього задання та їх властивості: рефлексивність, антирефлексивність, симетричність, асиметричність, антисиметричність, транзитивність, антитранзитивність.

3. Хоча поняття відповідності та відношення досить близькі, але вони мають суттєві відмінності. Не зупиняючись на цих відмінностях, які не є предметом нашого розгляду, приймемо наступне означення.

Означення: якщо у відповідності f множина відправлення Х співпадає з множиною прибуття У, то таку відповідність будемо називати відношенням між елементами множини Х.

Означення: бінарним відношенням, визначеним у множині Х, називається кожна підмножина декартового квадрату Х×Х=Х².

Як же можна задавати відношення? – оскільки відношення це відповідність, то його можна задавати тими самими способами, тобто за допомогою переліку, характеристичної властивості, таблиць, графів, графіків, формулою (аналітично). Які ж є типи відношень? – залежно від набору певних властивостей виділяють типи відношень, які ми визначимо за допомогою наступних означень.

Означення: відношення α, визначене у множині Х, називається рефлексивним, якщо кожний елемент множини Х перебуває у відношенні α сам з собою, тобто аαа.

Символічно наведене означення можна записати так: (хєХ)(аαа). Якщо відношення α рефлексивне, то говорять, що елементи множини Х мають властивість рефлексивності. Прикладами рефлексивних відношень є відношення подільності на множині чисел (а:а), рівності на множині фігур, паралельності на множині площин тощо.

Означення: відношення α, визначене у множині Х, називається антирефлексивним, якщо не кожен елемент множини Х перебуває у відношенні α сам з собою, тобто аαа.

Символічно наведене означення можна записати так: (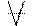хєХ)(аαа). Якщо відношення α антирефлексивне, то говорять, що елементи множини Х мають властивість антирефлексивності. Прикладами антирефлексивних відношень є відношення більше на множині чисел, перпендикулярності на множині прямих тощо.

Означення: відношення α, визначене у множині Х, називається симетричним, якщо для будь-яких а,вєХ із того, що аαв→вαа.

Символічно наведене означення можна записати так: (а,вєХ)(аαв→вαа). Якщо відношення α симетричне, то говорять, що елементи множини Х мають властивість симетричності. Прикладами симетричних відношень є відношення дорівнює на множині фігур, перпендикулярності на множині прямих тощо.

Означення: відношення α, визначене у множині Х, називається асиметричним, якщо для будь-яких а,вєХ із того, що аαв→вαа.

Символічно наведене означення можна записати так: (а,вєХ)(аαв→вαа). Якщо відношення α асиметричне, то говорять, що елементи множини Х мають властивість асиметричності.

Означення: відношення α, визначене у множині Х, називається антисиметричним, якщо для будь-яких а,вєХ із того, що (аαв^вαа)→(а=в).

Символічно наведене означення можна записати так:

(а,вєХ)(аαв^вαа)→(а=в). Якщо відношення α антисиметричне, то говорять, що елементи множини Х мають властивість антисиметричності.

Означення: відношення α, визначене у множині Х, називається транзитивним, якщо для будь-яких а,в,сєХ із того, що (аαв^вαс)→(аαс).

Символічно наведене означення можна записати так:

(а,в,сєХ)(аαв^вαс)→(аαс). Якщо відношення α транзитивне, то говорять, що елементи множини Х мають властивість транзитивності. Прикладами транзитивних відношень можуть бути: відношення подільності на множині чисел, відношення менше на множині кутів тощо.

Означення: відношення α, визначене у множині Х, називається антитранзитивним, якщо для будь-яких а,в,сєХ із того, що (аαв^вαс)→(аαс).

Символічно наведене означення можна записати так: (а,в,сєХ)(аαв^вαс)→(аαс). Якщо відношення α антитранзитивне, то говорять, що елементи множини Х мають властивість антитранзитивності.

Означення: відношення α, визначене у множині Х називається зв’язним, якщо для будь-яких аαв і а≠в випливає, що аαв або вαа.

Прикладом таких відношень є відношення більше, менше на множині чисел.

4. Як можна було б згрупувати різні за змістом відношення? – навколо певних наборів властивостей. У математиці відношення між елементами однієї множини поділяють принаймні на три групи: 1) відношення еквівалентності; 2) відношення порядку; 3) функціональні відношення. Розглянемо перші дві групи.

Означення: будь-яке рефлексивне, симетричне та транзитивне відношення f, визначене у множині Х, називається відношенням еквівалентності.

Прикладами відношень еквівалентності є відношення подібності на множині трикутників, паралельності на множині площин, «бути однокурсником» на множині студентів тощо. Як визначити, чи є задане відношення відношенням еквівалентності? – перевірити наявність у нього властивостей, які повинні бути у відношення такого типу. Покажемо це на конкретному прикладі.

Вправа: з’ясувати, чи є відношенням еквівалентності відношення «проживати на одній вулиці», задане на множині людей.

1) оскільки кожна людина проживає на одній вулиці сама з собою, то це відношення рефлексивне;

2) якщо людина А проживає на одній вулиці з людиною В, то і людина В проживає на одній вулиці з людиною А, тобто із (АαВ)→(ВαА);

3) якщо людина А проживає на одній вулиці з людиною В, а людина В проживає на одній вулиці з людиною С, то і людина А проживає на одній вулиці з людиною С, тобто із ((АαВ)^(ВαС))→(АαC).

Отже, відношення α:«проживати на одній вулиці», задане на множині людей, є рефлексивним, симетричним і транзитивним, а тому відноситься до відношень типу еквівалентності.

Розглядаючи поняття розбиття множини на підмножини, що попарно не перетинаються, ми з’ясували, що відношення «бути однокурсником» на множині студентів, розбило множину всіх студентів на п’ять підмножин. З’ясуємо властивості цього відношення. Легко бачити, що воно має властивості рефлексивності, симетричності і транзитивності (Чому?), а тому є відношенням типу еквівалентності. Сказане дає підстави припустити, що між розбиттям множини на класи, що попарно не перетинаються, і відношеннями типу еквівалентності існує певний зв'язок. Сутність цього зв’язку розкривається такою теоремою.

Теорема: для того, щоб відношення α дозволяло розбити множину Х на класи, що попарно не перетинаються, необхідно і достатньо, щоб відношення α було відношенням еквівалентності.

Оскільки у формулюванні цієї теореми є слова необхідно і достатньо, то доведення теореми складається із двох частин: 1) із доведення необхідності; 2) із доведення достатності. Цю теорему приймемо без доведення.

Означення: бінарне відношення α, визначене у множині Х, називається відношенням строгого порядку, якщо воно антирефлексивне, антисиметричне і транзитивне.

Прикладами відношень строгого порядку є: відношення «менше» у множині цілих чисел; відношення «бути старшим» на множині людей; відношення «бути вищим» на множині дерев тощо.

Означення: бінарне відношення α, визначене у множині Х, називається відношенням нестрогого порядку, якщо воно рефлексивне, антисиметричне і транзитивне.

Прикладами відношень нестрогого порядку є: відношення «більше або дорівнює» у множині раціональних чисел; відношення подільності на множині натуральних чисел тощо.

Означення: відношення порядку в множині Х називається відношенням лінійного порядку, якщо для будь-яких елементів х,уєХ виконується умова хαуÚуαх. Якщо ж відношення не має такої властивості, то його називають відношенням часткового порядку.

Прикладом відношення лінійного порядку є відношення «більше» чи «менше» на множині чисел.

Означення: якщо відношення α в множині Х є відношенням часткового порядку, то множину Х називають частково впорядкованою множиною.

Означення: якщо відношення α в множині Х є відношенням лінійного порядку, то множину Х називають лінійно впорядкованою множиною.

Лінійно впорядковані множини мають ряд властивостей. Нехай а,в,сєХ і множина Х лінійно впорядкована відношенням α. Якщо відомо, що аαвÙвαс, то говорять, що елемент в лежить між елементами а і с.

Означення: множина Х, яка лінійно впорядкована відношенням α, називається дискретною, якщо між будь-якими двома її елементами знаходиться лише скінченна множина елементів.

Прикладом дискретних множин є множини натуральних і цілих чисел.

Означення: множина Х, яка лінійно впорядкована відношенням α, називається щільною в собі, якщо для будь-яких двох різних її елементів існує елемент цієї множини, що лежить між ними.

Прикладом щільних в собі множин є множина дійсних чисел.

Переглядів: 3271