Малюнок № 1.20. Граф відповідності.

Поняття відповідності між елементами двох множин, бінарні відповідності, їх позначення та способи задання. Множина відправлення та множина прибуття відповідності. Образи і прообрази елементів і множин, їх позначення.

ПЛАН.

Змістовний модуль1.2. «Відповідності та відношення.».

МОДУЛЬ 1: «Множини. Відповідності Відношення.».

1. Поняття відповідності між елементами двох множин, бінарні відповідності, їх позначення та способи задання. Множина відправлення та множина прибуття відповідності. Образи і прообрази елементів і множин, їх позначення.

2. Типи відповідностей (порожня, повна, всюди визначена у множині відправлення, сюр’єктивна, інє’ктивна, функціональна відповідність або функція, відображення, бієктивна). Обернені функції та відображення.

3. Бінарні відношення між елементами однієї множини, способи їхнього задання та їх властивості: рефлексивність, антирефлексивність, симетричність, асиметричність, антисиметричність, транзитивність, антитранзитивність.

4. Відношення еквівалентності та порядку, їх властивості. Впорядковані множини. Зв'язок відношення еквівалентності з розбиттям множини на класи, що попарно не перетинаються.

ЛІТЕРАТУРА: [1] –с. 3-40; [2] –с. 11-88; [3] –с. 5-56.

1. Теорія множин вивчає множини та операції над ними. Розглядаючи це не цікавляться, як правило, природою елементів, із яких складається множина, способом задання множин і порядком розміщення елементів у множині. Разом з тим, математична теорія завжди прагне знайти своє застосування до розв’язування практичних задач. Як же це відбувається з теорією множин? – її застосовують до побудови математичних теорій, до розв’язування практичних завдань, розглядаючи множини, між елементами яких існують ті чи інші відношення. Прикладом таких відношень у повсякденному житті є родинні відношення між людьми, відношення на роботі між колегами, в математиці – це відношення паралельності, подільності, рівності тощо.

Слід зазначити, що поняття відповідності, відношення розуміють майже однозначно. Однак таке розуміння носить інтуїтивний, а не точний характер. Для вивчення різноманітних відношень між математичними об’єктами інтуїтивне поняття «відношення» слід уточнити, але так, щоб воно набуло цілком конкретного математичного змісту і в той же час не втратило своєї інтуїтивної сутності. Розглянемо дві скінченні множини Х={2, 4, 6, 8} і У={2, 3}. Утворимо із елементів цих множин впорядковані пари так, щоб перша компонента пари ділилася націло на другу компоненту. Отже, матимемо таку множину пар А={(2;2), (4;2), (6;2), (8;2), (6;3)}. Утворимо тепер декартів добуток множин Х і У: Х×У={(2;2), (2;3), (4;2), (4;3), (6;2), (6;3), (8;2), (8;3)}. Що можна сказати про множини А і Х×У? – множина А є підмножиною множини Х×У, тобто АÌХ×У. Враховуючи це, можна ввести таке означення поняття відношення:

Означення: бінарним відношенням, визначеним між елементами множин Х і У, називається будь-яка підмножина декартового добутку цих множин Х і У.

Означення: відповідністю між множинами Х і У називається трійка множин Х, У і GÌХ×У.

Множину Х називають множиною відправлення або областю визначення відповідності, множину У – множиною прибуття або множиною значень відповідності, а множину впорядкованих пар GÌХ×У, які перебувають у відповідності, - графіком відповідності. Домовилися відповідності позначати малими буквами грецького алфавіту α, β, γ, δ, ε та ін. Символічний запис α={GÌХ×У} означає, що задано відповідність між елементами множин Х і У. Якщо елементи пари (х;у) перебувають у відповідності α, то це позначають так: хαу і читають «елемент у відповідає елементу х у відповідності α». Інколи відповідності позначають і великими буквами латинського алфавіту R, S, T, наприклад: хRу, аSв тощо. Слід зазначити, що уже в початкових класах діти знайомляться з відповідностями та відношеннями. Так, молодші школярі розглядають відношення рівності, більше, менше тощо.

Коли ж відповідність вважається заданою та які способи задання відповідностей існують? – тоді, коли відносно будь-якої пари можна сказати належить чи не належить вона відповідності. Оскільки відповідність є підмножиною декартового добутку множин, то цілком логічно припустити, що відповідності можна задати всіма тими способами, якими задавався декартів добуток множин, а саме: 1) переліком всіх пар елементів, які перебувають у цій відповідності; 2) за допомогою характеристичної властивості; 3) таблицею; 4) рівнянням; 5) графіком; 6) графом. Не всі вказані способи задання відповідностей рівнозначні, а найзручнішим буде той, який потрібен саме для конкретної відповідності (пропонуємо виконати завдання № 38 для самостійної роботи!).

Отже, виникає запитання «чи однакові всі відповідності та як виділяти в них різні типи?». Перед тим, як знайти відповіді на ці запитання, розглянемо питання про образи та прообрази елементів у відповідності.

Означення: образом елемента аєА у відповідності αÌА×В називають множину тих елементів вєВ, для яких (а;в)єα.

Означення: прообразом елемента вєВ у відповідності αÌА×В називають множину тих елементів аєА, для яких (а;в)єα.

Домовилися образ елемента аєА у відповідності αÌА×В позначати α(а). Прообраз елемента вєВ при цій же відповідності αÌА×В будемо позначати так: α^-1(а). Нехай відповідність задана графом (див. малюнок № 1.20.).

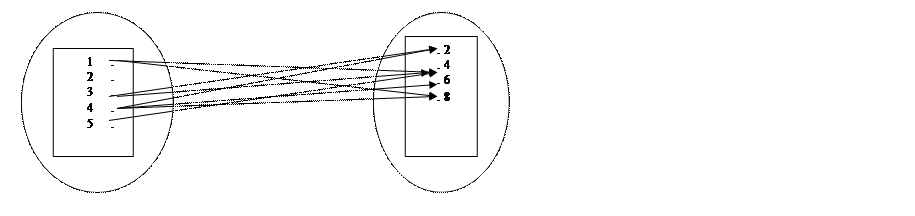
Користуючись малюнком, знайдемо образи і прообрази елементів, які перебувають у відповідності, заданій графом. α(1)={4, 8}, α(2)=Ø, α(3)={2, 4}, α(4)={2, 6, 8}, α(5)={4}, α^-1(2)={2, 3, 4}, α^-1(4)={2, 4, 5}, α^-1(6)= Ø, α^-1(8)={1, 4}. Із наведеного прикладу видно, що не всі елементи множини А мають образи у множині В. Так само як і не всі елементи множини В мають прообрази у множині А. враховуючи попереднє зауваження із базових множин А і В можна виділити дві підмножини: 1) підмножину α(А)={в/вєВ і існує таке аєА, що аαв}. Її називають множиною значень відповідності α і позначають α(А)ÌВ; 2) підмножину α^-1(В)={а/аєА і існує таке вєВ, що аαв}. Цю множину називають областю визначення відповідності α і позначають α^-1(В)ÌА. Таким чином, множина значень відповідності α(А) є об’єднанням образів всіх елементів множини А, а область визначення відповідності α^-1(В) є об’єднанням прообразів усіх елементів множини В.

2. Яке співвідношення може існувати між множинами G і Х×У? – 1) G∩Х×У=Ø; 2) GÌХ×У; 3) G=Х×У. Виходячи із цих співвідношень можна виділити наступні характерні типи відповідностей:

1) порожня відповідність, при якій G∩Х×У=Ø і α= Ø;

2) повна відповідність, при якій α=Х×У і у графі якої від кожного елемента множини Х йдуть стрілки до кожного елемента множини У;

3) відповідність всюди визначена у множині відправлення Х, тобто така, у якої GÌХ×У і для якої α^-1(У)=Х. Це означає, що всі елементи множини Х мають образи у множині У. На графі такої відповідності із кожного елемента множини Х виходить стрілка до якогось елемента множини У;

4) сюр’єктивна відповідність, тобто відповідність на всю множину прибуття У, причому α(Х)=У. При такій відповідності кожен елемент множини У має прообраз у множині Х. Для графа цієї відповідності характерно те, що із кожного елемента множини Х виходить стрілка і в кожен елемент множини У входить стрілка;

5) інє’ктивна відповідність – це така відповідність αÌХ×У, у якої прообрази елементів з множини У містять не більше одного елемента з множини Х. На графі такої відповідності в елементи множини У входить не більше однієї (одна або жодної) стрілки;

6) функціональна відповідність або функція, при якій образи елементів з множини Х або порожні, або містять лише один елемент. Граф цієї відповідності характеризується тим, що з кожного елемента множини Х виходить або одна стрілка, або не виходить жодної стрілки, але в елементи множини У може входити більше, ніж одна стрілка;

7) відображення – це всюди визначена функціональна відповідність, коли кожному елементу з множини Х відповідає єдиний елемент у множині У. Такі відповідності, тобто відображення, у свою чергу, поділяють на дві групи: а) відображення множини Х в множину У, коли у множині У є елементи, які не мають прообразів в множині Х. Граф такого відображення характеризується тим, що з всіх елементів множини Х виходять стрілки, але не в кожен елемент множини У входить хоча б одна стрілка; б) відображення множини Х на множину У, коли кожен елемент з множини У має прообраз у множині Х;

8) бієктивна або взаємно однозначна відповідність, яка одночасно всюди визначена, сюр’єктивна, інє’ктивна та функціональна, тобто це ін’єктивне та сюр’єктивне відображення.

У математиці доволі часто доводиться мати справу з оберненими об’єктами (обернені числа, обернені задачі, обернені теореми, обернені функції тощо). Отже, цілком доцільним є введення понять оберненої відповідності та оберненого відображення.

Означення: відповідністю, оберненою до відповідності αÌХ×У, називається така відповідність α^-1, яка є підмножиною декартового добутку множин У×Х і складається з тих і тільки тих пар (у;х), для яких (х;у)єα.

Якщо взяти функціональну відповідність і побудувати для неї обернену, то відповідь на запитання «чи буде одержана відповідність функціональною?» не завжди позитивна.

Означення: відображенням, оберненим до даного відображення f, називається таке відображення f^-1, у якого для кожного хєХ і уєУ, якщо f(х)=у, то f^-1(у)=х, тобто f^-1(f(х))=х.

У математиці доведено теорему, яка дає відповідь на запитання «які відображення мають обернені?».

Теорема: відображення fÌХ×У має обернене відображення f^-1 тоді і тільки тоді, коли відображення f – бієктивне.

Цю теорему приймемо без доведення.

Означення: відображення f називається оборотним, якщо воно має обернене відображення f^-1.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Малюнок № 1.19. Задання декартового добутку множин за допомогою графа.	\|	Відношення еквівалентності та порядку, їх властивості. Впорядковані множини. Зв'язок відношення еквівалентності з розбиттям множини на класи, що попарно не перетинаються.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.017 сек.